圆锥曲线中面积问题的解决策略

◎李逸凡

(石家庄二中，河北 石家庄 050051)

圆锥曲线中面积问题的解决策略

◎李逸凡

(石家庄二中，河北 石家庄 050051)

圆锥曲线面积的求解问题是高考热点,本文从恰当地选择底和高求三角形面积;对角线互相垂直的四边形面积为对角线之积的一半；不规则多边形的面积拆分为多个三角形的面积和等几方面进行了阐述.

圆锥曲线；面积求解；解决策略

一、恰当选择底和高表示面积

例1 过椭圆2x2+y2=2焦点的直线交椭圆于A,B两点，求△AOB面积最大值.

分析 表示△AOB面积时选择以OF为底，降低计算量.

二、求面积最值的策略

(一)数形结合

(二)将面积表示为函数，求最值

例3 设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合，l交圆A于C,D两点,过B作AC平行线交AD于点E.(Ⅰ)求点E的轨迹方程；(Ⅱ)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积取值范围.

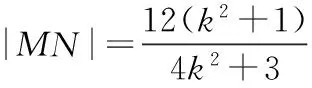
三、解决面积关系问题的策略

(一)高相同转化为底的关系

解 (1)P的轨迹方程为y=x2(x≠0,x≠-1).

(二)数形结合

(三)将面积关系表达为函数

解 (Ⅰ)椭圆方程x2+4y2=1.