基于安全系数的隧道二次衬砌支护设计新方法

张 伟

(太原理工大学矿业工程学院，山西 太原 030024)



·桥梁·隧道·

基于安全系数的隧道二次衬砌支护设计新方法

张 伟

(太原理工大学矿业工程学院，山西 太原 030024)

通过Phase2软件,对圆形隧道开挖过程中围岩的变形和衬砌结构内力进行了分析，确定了满足收敛约束法原理的二衬支护时机和满足安全系数为1.4的支护方案，并给出了其具体的应用步骤，该分析方法为定量设计和改进隧道二衬支护方案提供了新思路。

隧道，收敛约束法，开挖模拟，安全系数，支护方案

在进行岩石隧道开挖过程中，原岩应力重新分布，为控制和防止应力诱导下围岩的变形和破坏，需要进行合理的衬砌支护。文献[1]～[7]分别从经验类比、现场监测和数值模拟等方面提出了隧道开挖过程中支护的设计方法，总体来说，采用工程类比方法时，主观经验占据主导地位，采用数值计算方法对支护方案进行验证和对比选择时，只考虑了支护方案的安全性，而忽略了方案的经济性。本文结合相关文献和实际工程，基于虚拟支撑力模拟了隧道的渐进掘进过程，并通过支护强度包络线，最终确定了满足一定安全系数的二衬支护方案，实现了隧道的经济、安全施工，也为之后类似隧道的现场施工提供参考。

1 二衬施作时机及其控制

1.1 收敛约束法原理

“收敛—约束”法是国际隧道协会归纳出的一种解释围岩和支护动态作用过程的理论和方法。以隧道毛洞内壁的径向位移ur为横坐标，原岩应力下作用于洞室内壁的径向压应力σr为纵坐标，绘出表示二者关系的曲线，该曲线称为收敛线；以支护外缘的径向位移ur为横坐标，支护施加于洞壁的反力pi为纵坐标，绘出表示二者关系的曲线，该曲线称为约束线。在同一坐标平面内同时绘出收敛线和约束线，两条曲线的交点即可作为隧道二次衬砌设计计算的依据。其原理可用图1中的曲线来说明。

图1中，B点和C点分别表示支护时间过早和过晚，围岩压力较大，相应的支护费用较高，不合理；A点支护承受的围岩压力最小，是二次衬砌的最佳施作时间。图中下半部分曲线反映洞壁径向位移的变形速率。从图中可以看出，F点为开始支护时间，随着支护强度不断发展，洞壁径向位移变形速率基本达到稳定时支护完成。确定开始支护时间(F点)是隧道经济施工的关键，也就是确定F点对应的洞壁径向位移。本文通过数值模拟和经验公式法确定开始支护时的围岩变形量。

1.2 二衬支护开始施作时机

以一开挖半径为4 m的圆形隧道为例，隧道位于片岩中550 m深处，沿中间主应力方向(σ2=25 MPa)开挖，最大主应力值和最小主应力值分别为30 MPa和15 MPa，分别沿水平和竖直方向。片岩的单轴压缩强度UCS=50 MPa，地质强度指标GSI=50。本次模拟计算以霍克布朗准则为破坏准则，以支护断面为分析面，距离掌子面2 m。建模时，隧道中心到模型边界的距离取开挖半径的4倍，对模型边界施加完全约束。

为了考虑隧道开挖过程中的空间效应，本次模拟分10个载荷步，在每一个载荷步对开挖面施加支护反力，反力系数分别取1,0.8,0.4,0.2,0.2,0.08,0.04,0.03,0.01,0。模型的加载示意图如图2所示。

以隧道拱顶(0,4)为特征点，表1列出了各个载荷步下特征点的变形量。

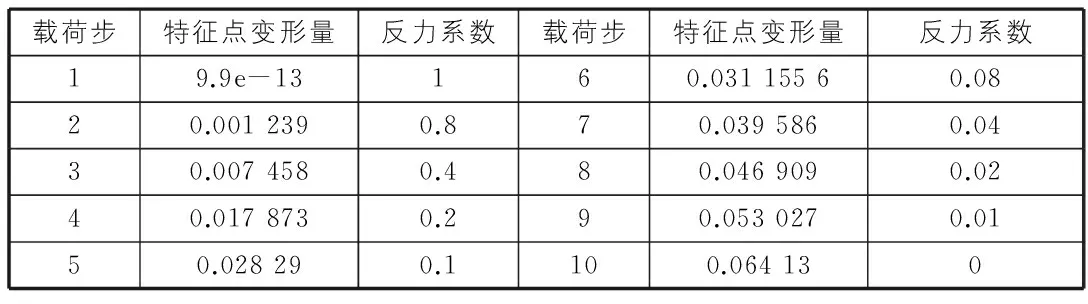
表1 特征点的变形量

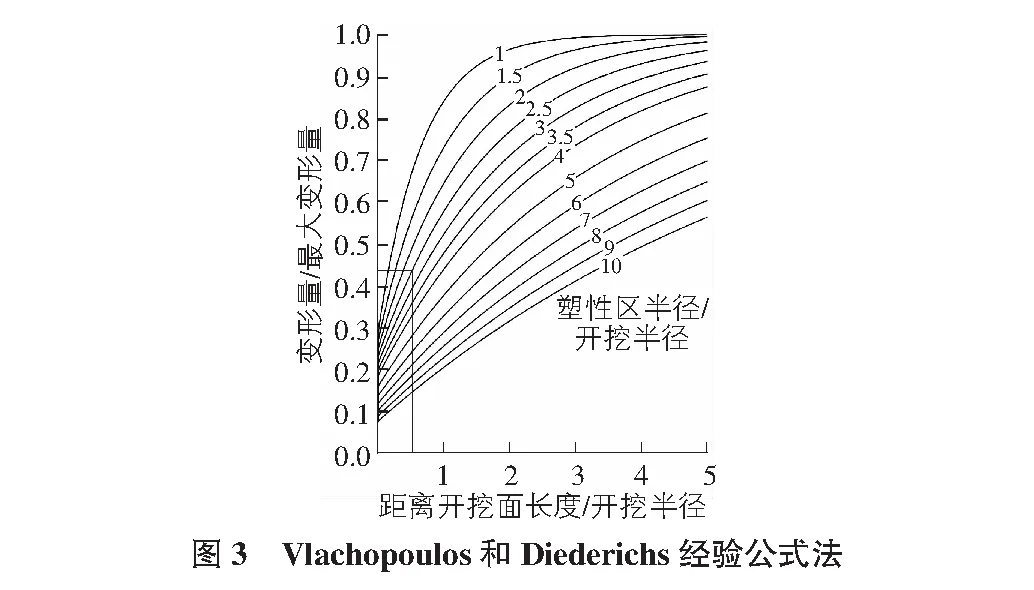
为了确定施作支护前围岩的变形量，Vlachopoulos和Diederichs提出了经验公式[8]，该公式对应在坐标系中的曲线如图3所示。图3中，横坐标表示支护断面离掌子面距离与隧道半径之比，纵坐标为变形量与最大变形量之比，曲线变量为塑性区半径与隧道半径之比。对模型进行分步计算，得到特征点的最大变形量为0.065 m，塑性区半径为9.5 m，已知支护断面距离掌子面2 m，此时对应的曲线和横、纵坐标值如图3中直线所示，即可得施作支护时特征点的变形量，为0.44×0.065=0.028 m。

查表1可知，当特征点的变形量为0.028 m时，对应的反力系数为0.1，因此应该在第5个载荷步对该断面开始支护。

2 满足安全系数的二衬支护方案

在有限元软件Phase2中，对给定的安全系数，可以绘制出以衬砌的轴向应力值为纵坐标，剪应力值或弯矩值为横坐标的支护强度包络线。支护完成后，将按照支护方案计算得到的衬砌内力值与支护强度包络线进行比对，当衬砌结构上所有位置的内力值都落在包络线之内，则该支护方案的安全系数大于设计值；反之，支护方案需要改进。

本次模拟在第5载荷步开始支护，要求安全系数达到1.4。支护设计为复合式衬砌结构，选择W100×19.3工字钢沿隧道边墙每隔2 m布置，混凝土选C25混凝土，厚度为100 mm，变形模量为25 GPa，泊松比为0.15。

2.1 衬砌内力分析

按照上述支护方案对隧道施加支护，得到衬砌结构上各个位置的内力值与支护强度包络线的关系如图4所示。图4分别绘制了安全系数为1,1.2,1.4的支护强度包络线。

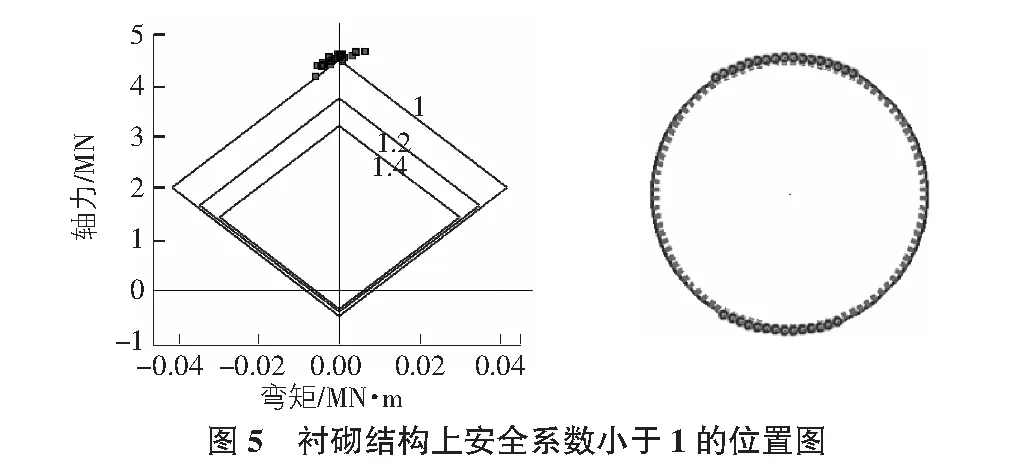
从图4可以看出，衬砌上部分位置的内力值落在包络线外面，因此该方案不能满足设计要求。以100 mm厚混凝土为例，设置安全系数范围为0～1，则包络图上仅显示安全系数小于1的点，这些点以及其对应在衬砌结构上的位置如图5所示。从图5可以看出，安全系数低于1的位置都集中于拱顶和拱底，这是由于开挖形成采空区，引起隧道周边应力集中，使得拱顶下沉，拱底向上抬起，容易发生开裂或塌陷现象。

2.2 方案改进

从上述方案的计算结果可以看出，该方案支护强度不足，需要改进。改进支护方案的方法有，选择高强度混凝土、工字钢材料或增大混凝土厚度。以W150×18工字钢和200 mm厚混凝土对方案进行改进并重复上述计算，得到衬砌结构内力值与支护强度包络线的关系如图6所示。

从图6可以看出，衬砌结构上所有位置的内力值都落在安全系数为1.4的包络线内部，即此时的支护结构已完全达到设计要求。因此，工程应用中，可以通过在数值软件中改变支护参数实现支护方案的定量改进，并能直观地判断改进后的支护是否有效。同时，通过绘制支护强度包络线可以快速找出支护结构的薄弱位置，对薄弱位置进行特殊施工也可达到改进支护效果的目的。

3 结语

本文通过Phase2软件模拟隧道的开挖支护过程，从满足支护安全系数考虑，为隧道支护设计提供了一个新方法。在本文中，主要得到以下几个结论：1)对于本次模拟，虚拟支撑力为0.1倍原岩应力时，为开始支护的最合理时机。2)通过支护强度包络线可以直观地判断衬砌结构的支撑作用是否满足设计要求；对于本次模拟，当采用W150×18工字钢，200 mm厚混凝土支护时，支护的安全系数已达到1.4。3)有限元软件Phase2可以基于给定的安全系数判断支护方案是否满足要求，并且能够准确捕捉衬砌结构的薄弱位置，据此对薄弱位置加强支护，可以达到支护方案的经济性和安全性。

[1] JTGD 70—2004，公路隧道设计规范[S].

[2] 李洪斌．南湾隧道深基坑支护方案比选[J].广东土木与建筑，2008(4):45-47．

[3] 邓少军，阳军生，张学民，等．浅埋偏压连拱隧道施工数值模拟及方案比选[J].地下空间与工程学报，2005，1(6):940-943．

[4] 冯夏庭，江 权，向天兵，等．大型洞室群智能动态设计方法及其实践[J].岩石力学与工程学报，2011，30(3):433-448．

[5] 乔春生，魏莉萍．岩石地下工程锚喷支护设计的人工智能方法及其集成[J].岩石力学与工程学报，2004，23(5):781-785．

[6] 王述红，朱浮声，张 凯，等．岩体隧道施工过程智能辅助决策系统的实现[J].岩石力学与工程学报，2002，21(4):590-594．

[7] 孙海涛，刘东燕，黄声树，等．隧道支护时机智能决策方法研究[J].重庆建筑大学学报，2007，29(3):78-82．

[8] Hoek, E., Carranza-Torres,C.,Diederichs,M.S,et al.Integration of geotechnical and structural design in tunneling[A].Proceedings University of Minnesota 56th Annual Geotechnical Engineering Conference[C]. Minneapolis,2008：1-53.

A new design method of tunnel secondary lining support based on safety factor

Zhang Wei

(Taiyuan University of Technology, College of Mining Engineering, Taiyuan 030024, China)

This paper uses Phase2 software to analyze the deformation and lining structure internal force of the surrounding rock for a circular tunnel. The secondary lining support timing and the support scheme with 1.4 safety factor are determined based on the convergence constraint method. The analytical method provides a new idea for the design and improvement of the secondary lining support.

tunnel, convergence-confinement method， excavation simulation， safety factor， support scheme

1009-6825(2016)34-0156-03

2016-09-25

张 伟(1961- ),男，硕士，高级工程师

U451.4

A