基于倒频谱的无噪声运动模糊图像快速复原算法

魏　鑫，陈广锋

(东华大学 纺织装备教育部工程研究中心， 上海 201620)

基于倒频谱的无噪声运动模糊图像快速复原算法

魏鑫，陈广锋

(东华大学 纺织装备教育部工程研究中心， 上海 201620)

摘要：针对当前运动模糊图像复原算法主要集中在非实时性研究，着重考虑算法的执行质量而不考虑算法执行效率的问题，提出了基于倒频谱的无噪声图像的快速复原算法.该算法对无噪声模糊图像进行倒频谱处理，从倒频谱图中直接得到图像的模糊方向和模糊距离.对于尺寸较大的图像，在执行倒频谱算法前先使用双线性插值算法实现图像压缩，再进行倒频谱操作.通过比较各种复原算法的执行效率及效果，采用维纳滤波对图像进行复原.通过对多幅模糊图像进行仿真复原试验，在获得了良好的复原效果的同时也取得了较高的执行效率.

关键词：运动模糊； 双线性插值； 倒频谱； 维纳滤波； 图像复原

成像器件对目标成像时，在曝光时间内感光介质与被照物影像间存在相对运动而带来的成像模糊称为运动模糊[1].对传送带上的工件进行表面缺陷检测时，得到的必然是具有运动模糊特性的图像.

运动模糊图像复原已得到广泛的重视和研究，并且国内外研究提出的各种复原方法已经取得了一定的成效[2].运动模糊图像的退化模型中使用最广泛的为点扩散模型，众多研究者研究了很多获取点扩散函数(PSF)参数的方法.有的方法通过鉴别曲线来求图像运动模糊的长度，即将微分自相关图像各列实施求和，得到一条鉴别曲线，曲线上会出现一对共轭的相关峰，这对相关峰对称分布在零频尖峰两侧，鉴别出这两个相关峰的位置，就可以得出运动模糊点扩散函数的尺度[3].文献[1]中使用倒频谱和Radon(随机)变化的方法确定了PSF参数.文献[3]利用测量傅里叶谱中黑带间隔距离确定模糊长度，使用图像灰度值方向微分确定模糊方向.文献[7]中使用Garbor滤波器和模糊图像的傅里叶谱进行卷积，通过比较不同方向的响应来得到模糊角度，使用径向基函数神经网络(RBFNN)确定模糊长度.文献[8-9]提出了通过计算模糊图像梯度的功率谱来获得频域内明暗相间的线条，计算线条间的距离和线条方向来获取PSF参数，本质上与其他方法无区别.文献[10]所提出的图像去模糊方法的创新之处在于图像复原部分使用了基于全变分的复原算法，该算法对于运动模糊和离焦模糊情况均有很好的复原效果，但效率较低，256像素×256像素的Cameraman图像需要使用1.7 s才能实现图像的复原.以上算法都试图成为通用算法，考虑的因素较多，造成算法的效率低下.虽有文献[10]研究了快速复原算法，但这种快速是相比其他算法的，并不是绝对的快速，即不适用于传送带上图像的实时复原.

在专门用于传送带的影像测量系统中，模糊图像中很少存在噪声影响，但对算法的效率要求高.本文针对这种特殊需求，综合考虑常见压缩算法的优缺点，提出了先使用双线性插值算法对图像进行压缩，保证了图像的信息熵不会过度减小，再使用倒频谱法获取PSF参数，最后比较各种复原算法的执行效率和效果，选择最符合实时在线测量系统的复原算法.

1图像压缩

用于实时在线检测的工业相机像素往往不高，但一般也有100万像素.这样的相机拍出来的图像尺寸也较大，增大了算法的计算量，延长了计算时间，因此在倒频谱前需要对图像进行压缩处理.

1.1常见压缩算法分析

常见的图像压缩算法有霍夫曼编码、离散余弦变换(DCT)、小波压缩和双线性插值算法等.前两种压缩算法仅改变图像的编码冗余，图像尺寸并不下降，不仅无法减少后续算法的计算量，而且由于图像质量下降，导致图像的信噪比降低，反而影响倒频谱算法的准确度.而小波图像压缩的特点在于压缩比高、压缩速度快，压缩后能保持信号与图像的基本特征不变[4].但是小波压缩时相当于对原图添加了低通滤波器，同时对原图做“下二采样”(即序列仅保留下标为偶数的元素)，因此，经过小波压缩的图像必然丢失了原图中的高频信息.

1.2双线性插值算法

在图像的双线性插值算法中，目标图像中新创造的像素值，是由源图像位置在它附近2×2区域的4个临近像素的值通过加权平均计算得出的.此算法也具有低通滤波器的性质，使高频分量受损，可能使图像轮廓变得模糊.双线性插值示意图如图1所示.

图1　双线性插值示意图Fig.1　Bilinear interpolation schematic

如图1所示，x轴方向的线性插值为

(1)

其中：R1=(x,y1).

(2)

其中：R2=(x,y2).

y轴方向的线性插值为

(3)

由于双线性插值算法综合考虑了临近像素的影响，对高频分量的过滤较少，且算法直接在空域操作，因此，算法压缩效果较好，执行效率较高.

1.3两种压缩算法下图像质量及压缩效率对比

由于压缩后的图像尺寸已经改变，因此，均方误差、峰值信噪比等全参考质量评价方法不适用.本文使用信息熵对小波压缩和双线性插值这两种算法压缩后的模糊图像质量进行评价.图2为接插件壳体的模糊图及其分别经小波压缩和双线性插值后得到的压缩图像.

(a) 模糊原图

(b) 小波压缩图

(c) 双线性插值压缩图

从图2中很难直观发现两种压缩算法所得图像质量的区别，不同压缩算法的压缩效率及效果对比如表1所示.由表1中的数据可看出，双线性插值算法较小波压缩算法在效率上有了很显著的提高. 从图像质量角度来说，相比于双线性插值算法，小波压缩算法处理后的信息熵增大更多，即图像质量下降更为剧烈.对两种压缩算法执行过程分析可知，因小波压缩算法中存在“下二采样”操作，破坏了原图像的连续性，导致图像信息熵增大，图像质量下降；双线性插值算法相当于对图像进行了低通滤波操作，因此图像被轻微模糊，信息熵略有下降.鉴于双线性插值算法的执行效率高，以及压缩后图像质量下降较少的优点，本文在执行后续倒频谱和复原算法前使用该算法进行图像压缩.

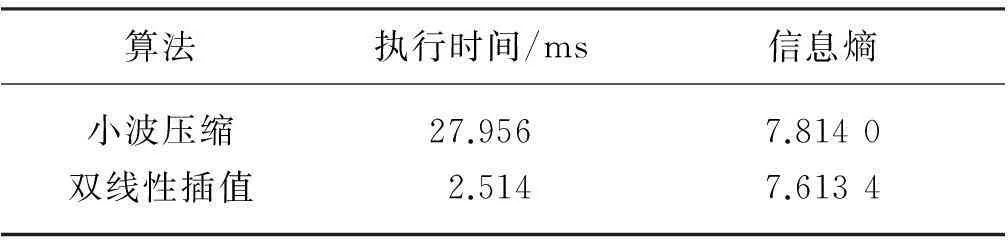
表1　不同压缩算法的压缩效率及效果对比

注：未模糊图像信息熵为7.5954，模糊未压缩图像信息熵为7.6206， 尺寸为816像素×219像素.

2图像的退化和复原

2.1图像的退化和复原模型

图像的运动模糊过程可以被模型化为一个退化函数和一个加性噪声项[1].输入图像f(x,y)，得到退化图像g(x,y).假设H是一个线性、位置不变性的过程，空间域给出的退化图像可由式(4)给出.

g(x,y)=h(x,y)*f(x,y)+n(x,y)

(4)

其中：h(x,y)为退化函数的空间描述；*为空间卷积.对应频域下的描述为

G(u,v)=H(u,v)F(u,v)+N(u,v)

(5)

其中：大写字母项为式(1)中相应项的傅里叶变换.因为本文并不考虑噪声的影响，故式(5)中N(u,v)=0. 图3为图像的退化和复原过程图.

图3　图像的退化和复原过程Fig.3　Image degradation and restoration processes

2.2匀速直线运动退化模型

在图像采集过程中被拍摄物和摄像机之间的相对运动会造成图像的模糊.假设T表示曝光时间，f(x,y)表示匀速直线运动的物体，g(x,y)表示运动模糊产生的退化图像，x0(t)和y0(t)分别表示物体在x轴和y轴方向上运动时的变化分量，匀速直线运动模糊图像的退化模型可以表示为

(6)

对式(6)进行傅里叶变化后并整理，可得

(7)

对比式(5)和(7)可知，

(8)

式(8)即为任意方向匀速直线运动模糊图像退化模型的传递函数.

3倒频谱法鉴定模糊参数

3.1倒频谱定义及意义分析

倒频谱最初定义来自文献[5]，定义为

Cg(p,q)=F-1[log10|G(u,v)|]

(9)

参阅文献[1-2]，倒频谱可表示为

8．宋高似孙《夜宿金庭洞》：“夙闻桐柏山，下有金庭洞；五云所出没，千翠相迎送；川明芝自烨，夏冷雪犹冻；沙泉泾阳水，苍碧孕阴峒；天光抱琼台，神力扶兰栋；其左闻苍蚪，其西翔紫凤……”[14]

Cg(p,q)=Cf(p,q)+Ch(p,q)

(10)

其中：Cf(p,q)为原始图像倒频谱；Ch(p,q)为点扩散函数倒频谱.

图2中各图所对应的倒频谱图如图4所示，其模糊角度为60°，模糊距离为20像素.

(a) 原图倒谱图

(b) 小波压缩图倒谱图

(c) 双线性插值压缩图倒谱图

图4中的亮点对应于原图中的低频分量，亮线的方向就对应于原图中的低频方向.对于运动模糊图像，模糊方向上的像素处于低频，垂直于模糊方向则对应图像的高频部分.因此对应图4中各图，60°方向有条很明显的亮线.不同之处在于，图4(a)中没有其他方向的亮线，图4(b)有很明显的水平和垂直方向的亮线，图4(c)中有微弱的水平和垂直方向的亮点.其原因在于：在图4(b)中，原图的中的高频部分经小波压缩后被剔除，模糊方向上低频的主导优势被弱化，其他方向上的低频得以显示；而双线性插值算法也有低通滤波器的效果，故图4(c)的原图也被稍微模糊，导致其水平方向出现亮点.

3.2模糊参数获取及精度比较

在图4(a)和4(c)中，可以直接找到倒谱中的最小值点(有两个)，两点的连线方向即为运动模糊方向，两点连线的距离为模糊长度的两倍.而图4(b)受水平、垂直方向亮点的影响，无法直接通过找最小值点来得到模糊参数.文献[2]使用了Canny算子和灰度形态学来确定两个最小值点的位置，显然效率低下.

在不同模糊方向(α)及模糊长度(L)的条件下，先使用双线性插值算法压缩图像，再使用倒频谱得到的PSF参数，结果如表2所示.

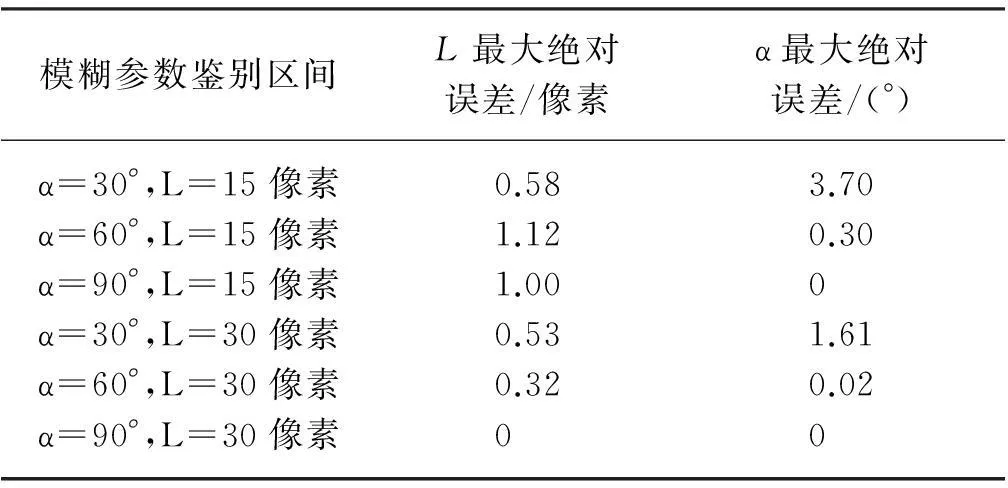
表2　不同测试条件的鉴别结果精度比较

本文虽然讨论的是无噪声运动模糊图像的复原，但是从对图4的分析中还可以得到以下结论，即当添加一定程度的高斯噪声时，用倒频谱法仍可以准确计算出PSF参数.高斯噪声在图像中属于高频，会影响原图的低频部分，故在倒频谱图中不会显现，但却缩短了倒频谱图的亮线.当图像噪声强度一定时，原图中运动模糊方向的低频仍占主导地位，倒频谱中仍有亮线.噪声强度再大时，低频部分也被噪声淹没，倒频谱图上只有最中心的一个亮点，从而无法判定PSF参数.

对接插件壳体的模糊图的添加均值为0和方差为0.001的高斯噪声，再用本文的方法计算PSF参数，计算出模糊角度为60.945°，模糊长度为20.61像素，其倒频谱图如图5所示.对比图4(c)和5可发现，图5中亮线的长度明显缩短.

图5　添加高斯噪声的倒频谱图Fig.5　Cepstrum with Gaussian noise added

4运动模糊图像复原试验

经典的图像复原算法有逆滤波、维纳滤波、规则化滤波和Richardson-Lucy滤波.逆滤波复原要求模糊图像的信噪比高，规则化滤波要求对原始图像和噪声的一些统计特性有先验知识，Richardson-Lucy滤波虽是目前应用最广泛的非线性迭代图像复原技术，但多次迭代造成算法效率下降.综合图像复原质量和效率，本文选择维纳滤波.

4.1仿真运动模糊图像复原

图6为接插件壳体的原图(816像素×219像素)、模糊图、未压缩复原图和压缩后复原图的对比，其模糊角度为60°，模糊长度为20像素.

(a) 原图

(b) 模糊图

(c) 未压缩复原图

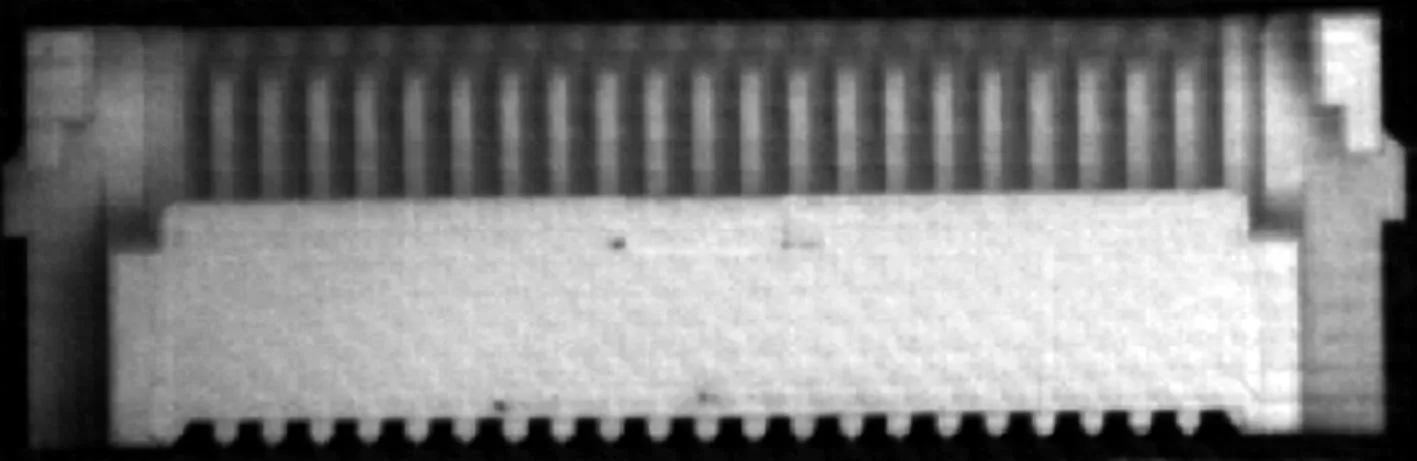
(d) 压缩后复原图

图7为Cameraman的原图(256像素×256像素)、模糊图、未压缩复原图和压缩后复原图的对比，其模糊角度为60°，模糊长度为20像素.

(a) 原图

(b) 模糊图

(c) 未压缩复原图

d) 压缩后复原图

4.2实际模糊图像复原

图8和9分别为流水线上不同时刻工件的实拍图(696像素×514像素)和压缩后复原图对比，分别为试验3和4，且图8测得模糊角度为90°，模糊长度为10像素，图9测得模糊角度为92.71°，模糊长度为10.05像素.

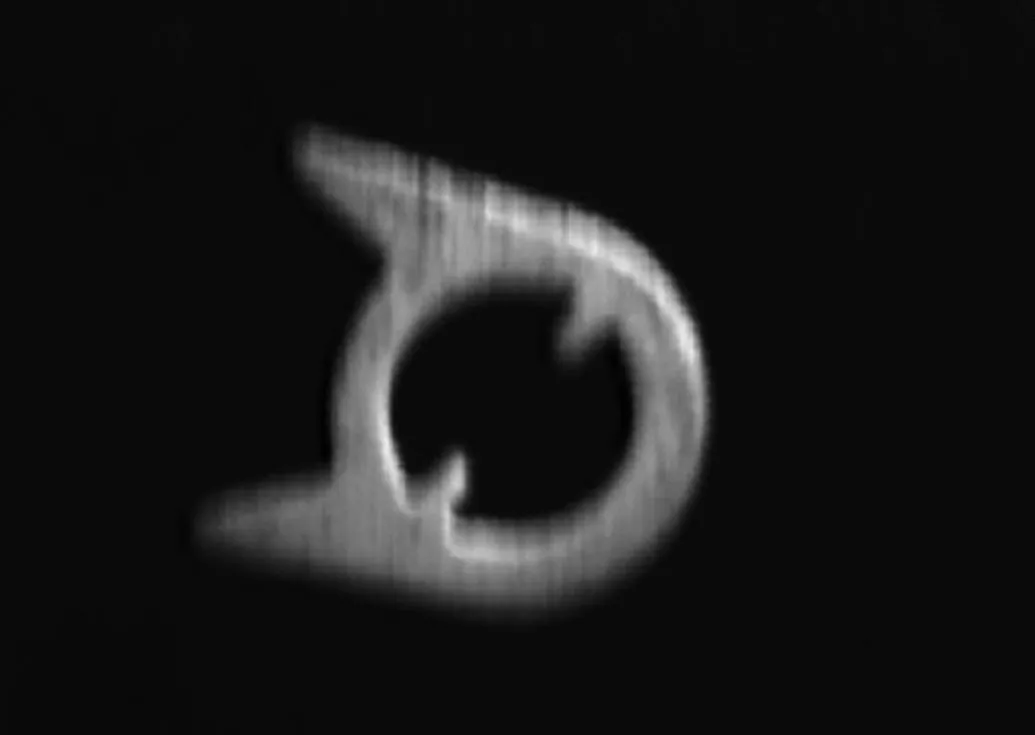
(a) 实拍图

(b) 复原图

(a) 实拍图

(b) 复原图

表3分别计算了4组试验的复原效率和复原后图像的信息熵.其中算法执行时间包括双线性插值算法压缩图像时间、压缩图像倒频谱并获得的PSF参数时间和维纳滤波复原时间.以试验4为例，本文算法3部分的执行时间分别为1.8，6.5和9.4ms，如若未执行图像压缩，3部分的执行时间分别为0，26.1和37.5ms.由此可见，模糊图像复原的执行时间主要花费在复原算法上.

表3　不同试验的效率和效果对比

在不使用压缩算法的情况下，文献[1-3,5,7-9]中获取PSF参数的方式一般包括傅里叶变化、滤波和形态学处理，它们的处理步骤均要多于本文的倒频谱后取最小值法的处理步骤.由于双线性插值属于计算机擅长的线性运算，在保证图像质量的情况下将图像的大小压缩至原来的1/4只需很短的时间，但后续操作的效率可以提高4倍.文献[10]提出的快速复原算法的快速性是相对其他非线性复原方法的，虽然复原效果较好，但在模糊类型已知且不考虑噪声的情况下，效率远不及维纳滤波复原.综上所述，本文方法在获取PSF参数和复原时都有更高的执行效率.

5结语

不同于以往只重视运动模糊图像复原效果的研究，本文提出了先对模糊图像进行双线性插值压缩，再经倒频谱处理后快速地得到PSF参数，最后利用维纳滤波对图像进行复原的算法.该算法具有快速性和一定的抗噪声能力，对比试验的结果也表明算法具有良好的复原效果.本文试验得到的执行时间是在Matlab中直接得到的，并未使用编译后的函数，因此，如果使用OpenCV进行相同的操作，算法会更加高效，可以满足实时在线复原的应用需求.

参考文献

[1] 谢飞，车宏，蔡猛. 一种基于倒频谱鉴别模糊参数的图像复原算法[J]. 电光与控制，2011，18(7)：49-54.

[2] 王鹏飞. 运动模糊图像复原算法研究[D]. 重庆：重庆大学光电工程学院，2013：2.

[3] 郑辉. 运动模糊图像复原技术的研究与实现[D]. 长沙：国防科学技术大学计算机学院，2007：16-19.

[4] 张德丰. Matlab数字图像处理[M]. 2版. 北京：机械工业出版社，2013：253-254.

[5] ROM R. On the cepstrum of two-dimensional functions(Corresp)[J]. IEEE Transactions on Information Theory，1975，21(2)：214-217.

[6] GONZALEZRC， WOODSR E. Digital image processing[M]. 3版. 北京：电子工业出版社，2013：515-523.

[7] DASHR， MAJHIB. Motion blur parameters estimation for image restoration[J]. Optik，2014，125：1634-1640.

[8] GOVINDAN S， SARAVANAKUMAR S. Fast blur kernel estimation with texture preserving DRD for motion deblur[J]. Procedia Engineering，2012，38：442-447.

[9] MICHAL D， LIBOR M， TOMAS F. Blurred image restoration: A fast method of finding the motion length and angle[J]. Digital Signal Processing，2010，20：1677-1686.

[10] FANY H， WEIX M， QINS Y. Fast and robust deblurring method with multi-frame images based on PSF estimation and total variation optimization[J]. Optik，2013，124：2285-2291.

Fast Restoration Algorithm of Noise-Free Images Based on Cepstrum

WEIXin,CHENGuang-feng

(Engineering Research Center of Advanced Textile Machinery, Ministry of Education, Donghua University, Shanghai 201620, China)

Abstract:For the problem of current motion blurred image restoration focusing on non-real-time research, that is, focusing on the quality of the algorithm rather than considering the executed efficiency of the algorithm, a fast restoration algorithm of noise-free images based on cepstrum is raised. The blur direction and blur length are directly generated from the cepstrum, which is elaborated by the algorithm of noise-free image. For images with large size, a compression of bilinear interpolation is completed initially then goes the cepstrum of the compressed image. The wiener filtering for image restoration is selected under the comparison with various restoration algorithm, regarding the efficiency and effectiveness. Hence through the deblur experiments on blurred images, restoration effect can be demonstrated along with the high performance efficiency.

Key words:motion blur; biliner interpolation; cepstrum; wiener filtering; image restoration

文章编号：1671-0444(2016)02-0228-06

收稿日期：2015-04-01

基金项目：中央高校基本科研业务费专项资金资助项目(2232013D3-44)

作者简介：魏鑫(1990—)，男，安徽蚌埠人，硕士研究生，研究方向为智能检测. E-mail: weixin3032503@163.com 陈广锋(联系人)，男，副教授，E-mail: chengf@dhu.edu.cn

中图分类号：TP 753

文献标志码：A