关于“情境—模型”双向建构的初中数学教学设计探析

曹瑾

摘 要： 本文对“情境—模型”双向构建在初中数学中的应用进行分析，提出了通过情境创设培养学生的学习兴趣，同时使学生在脑海中构建出一定的思维模型。

关键词： 初中数学教学 教学情境 思维模型 双向建构

伴随着新课改的不断深入，情境创设被不断应用到初中数学教学中。将情境和模型进行双向构建，通过情境的创设提高学生学习积极性，使学生在脑海中形成一定思维模型，让学生对初中数学知识理解得更透彻，提升初中数学教学水平[1-2]。

1.创设趣味化教学情境

“兴趣是最好的老师”，学生对学习材料是否感兴趣是决定学生学习效果好坏的关键性因素。要想使学生积极主动地进行初中数学学习，提高学生学习效率，最有效的方式就是培养学生的学习兴趣。

例如在学习“三角形形式性判定”有关内容时，为了使学生的学习兴趣有所提升，教师可以在课前导入有关的故事，吸引学生的注意力。教师为学生描述了一个场景：古希腊有位哲学家去埃及旅行，并参观了金字塔。这位科学家向大祭司提问，是否知道胡夫金字塔的高度，大祭司没能回答这一问题，因为大祭司从来没有思考过这一问题。接下来请同学们帮助大祭司思考这一问题。听了这个故事，学生的学习热情被调动起来，开始积极主动地对这一问题进行思考。然后教师对学生进行引导，让学生带着这一问题进行“三角形相似性”相关内容的学习。与此同时，教师将学生分成若干个小组，然后通过小组讨论的形式从数学教材中查找答案。通过这样的方式，让学生带着疑问和兴趣对这一内容进行学习，对三角形的相似性有了充分了解，学生在脑海中形成一个知识体系。接下来教师带领学生一同对这一问题进行解答。这就为学生构建了一个生动形象的故事情境，使整个课堂充满趣味性。将这一故事导入到“三角形相似性”课堂内容中，既能避免因为学生缺乏逻辑感导致学习兴趣下降，又能使学生对数学知识产生更深刻的理解，从而将数学知识应用到日常生活中。

2.通过情境创设，培养学生语言能力，构建空间模型

在初中数学教学过程中，学生开始接触空间思维。因此最初的教学主要是让学生以了解为主，利用最简单的方式和最基础的题目让学生对数学知识形成空间观念，同时教师注重培养学生空间位置能力，避免学生对空间物体的理解出现错误。

例如，小明骑自行车从家出发，先向东行驶了500m，达到十字路口后，再向南行驶了1000m达到了小明的奶奶家。这时教师让学生画出小明的行驶路线，同时用语言描述小明回家的路线。

大部分学生这时可以完成第一部分内容，但是让学生描述路线较困难。这一问题出现的主要原因是学生的空间思维能较差。在这一过程中，教师通过多媒体技术对学生进行引导，将这一路线通过立体图形的方式展现在学生面前，从而帮助学生准确地描述回家的路线。教师让学生在课下充分了解物体和物体之间的方位关系，进而使学生在脑海中构架出空间模型。

3.利用情境教具教学，通过生活化方构学生思维模型

传统的初中数学是教师按照考试大纲和教材进行讲解，学生对数学知识被动接受，教师和学生之间缺少交流。并且教师的教学方式较单一，对于不同的教学内容采取相同的教学方法。这样的教学方式很难使学生的空间思维得到开发。实际教学过程中，教师采用科学的教学方法可以提高学生的空间思维能力，情境教学法和教具演示都能在一定程度上提高学生的空间思维能力。例如，在讲解“三视图”有关内容时，教师可以先为学生准备几个盒子，通过现场演示让学生从不同方向对盒子进行观察，观察结束后，教师为学生进行讲解，从而让学生对“三视图”的内容有充分了解。然后，教师让学生结合自己对这一内容的理解，自主画出“三视图”，再利用盒子为学生进行现场演练，让学生真切感受到实际物体和自己所画出“三视图”之间的差距，最后引导学生找出自己的错误，并在其中分析出一定的规律，这样能有效培养学生的空间思维能力。

4.通过情境培养学生的模式化空间思维

初中生空间思维能力的提高，需要教师进行一定的引导，只有这样，学生才能牢固掌握方法，从而达到事半功倍的效果。在初中数学教学过程中，教师要注重培养学生的空间思考能力。可以为学生创设一定的情境，从而让学生通过这一情境对问题进行思考。例如对几何问题进行学习的过程中，三角形ABC（①）中，AB=AC，AC=BC，D是BC的中点，图（②）中BC外的任何一点，使BE=CE，△ABE和△ACE全等。这一题目中，学生对①进行分析，所得出的图形是等边三角形，从而在②中产生一定的空间思维，并对图形具备的结构进行适当丰富，从而使学生产生联想，只要将AE进行连接，就能证明两个三角形全等。在这一过程中，学生看到图形之后，会产生一定联想，空间思维能力得到一定的提高。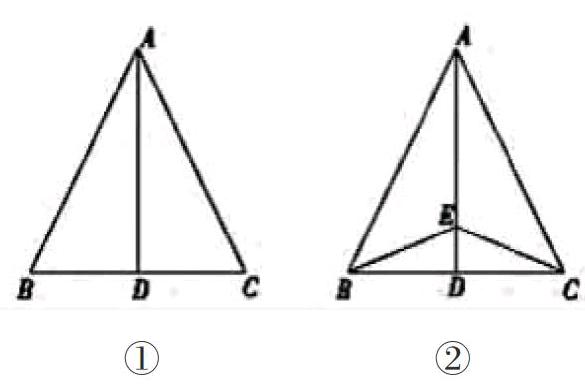

结语

初中数学较抽象，通过情境的创设可以使数学知识变得具体和直观，进而让学生在脑海中形成一个空间模型，使学生对数学知识的理解更透彻。在初中数学教学过程中，教师利用多媒体，将抽象的数学知识通过直观的方式展现出来，使学生对这一知识理解得更透彻，并形成清晰的解题思路。

参考文献：

[1]杨元超.基于“情境—模型”双向建构的初中数学教学设计研究[D].重庆师范大学，2015.

[2]刘学军.让学生在情境中建构数学模型——苏教版“方程的意义”教学设计与反思[J].基础教育论坛：综合版，2015（10）：47-48.