频率分布直方图常见错误剖析

徐锐

频率分布直方图是用来刻画样本数据分布的重要工具之一，也是用样本估计总体的常用方法. 整个制图过程操作性强，图形简洁美观、分布直观，也适用于计算机绘图，所以在各行业的数据处理中应用广泛.

《普通高中数学课程标准》对频率分布直方图的具体要求是：通过实例体会分布的意义和作用，会列频率分布表、画频率分布直方图表示样本数据，并体会其特点. 会用样本的频率分布直方图估计总体分布，会用样本的频率分布直方图估计总体的基本数字特征. 简单地说，就是能“制图”，会“用图”. 而同学们在解题中的错误也主要发生在这两个过程中.

分组、频数统计等环节出错

例1 某市2016年4月1日～4月30日对空气污染指数的监测数据如下（主要污染物为可吸入颗粒物）：

61，76，70，56，81，91，92，91，75，81，88，67，101，103，95，

91，77，86，81，83，82，82，64，79，86，85，75，71，49，45.

请对以上数据进行分组，并统计每组频数.

错解1 首先计算这组数据的极差为103-45=58，将组距定为10，组数定为不是整数，无法分组.

错解2 计算这组数据的极差为103-45=58，将组距定为10，组数定为6，则将30个数据分为[45，55]，[55，65]，[65，75]，[75，85]，[85，95]，[95，105]这6组，得到每组的频数分别为2，3，5，12，9，3.

正解 计算这组数据的极差为103-45=58，将组距定为10，不是整数，可以分为六组. 在分组时，将30个数据分为[45，55），[55，65），[65，75），[75，85），[85，95），[95，105] 这6组，得到每组的频数分别为2，3，3，11，8，3.

点拨 若“极差/组距”为整数，则此整数即为组数. 若“极差/组距”不为整数，则“极差/组距”的整数部分+1即为组数. 分组时每组所在区间一般是选择“左闭右开”，而不是“双闭”或“双开”，以防止某些数据漏选或某些数据被多次计入不同小组，从而导致频数统计失误. 为防出错，可以检查各组频数之和是否等于样本容量. 如错解2中，频数之和为2+3+5+12+9+3=34>30，错因是分组时所取区间为闭区间，因而75、85、95三个数据被重复计数了.

例2 2000辆汽车通过某一段公路时的时速的频率分布直方图如图，时速在的汽车大约有（ ）

A. 30辆 B. 60辆

C. 300辆 D. 600辆

错解 辆，选B.

正解 对应的频率为，对应汽车数量为辆，选D.

答案 D

点拨 本例错解在于将频率分布直方图的纵坐标“”误认为是“频率”. 正确的理解是频率分布直方图中每个矩形的高等于该组的，每个矩形的面积是该组的频率.

练习

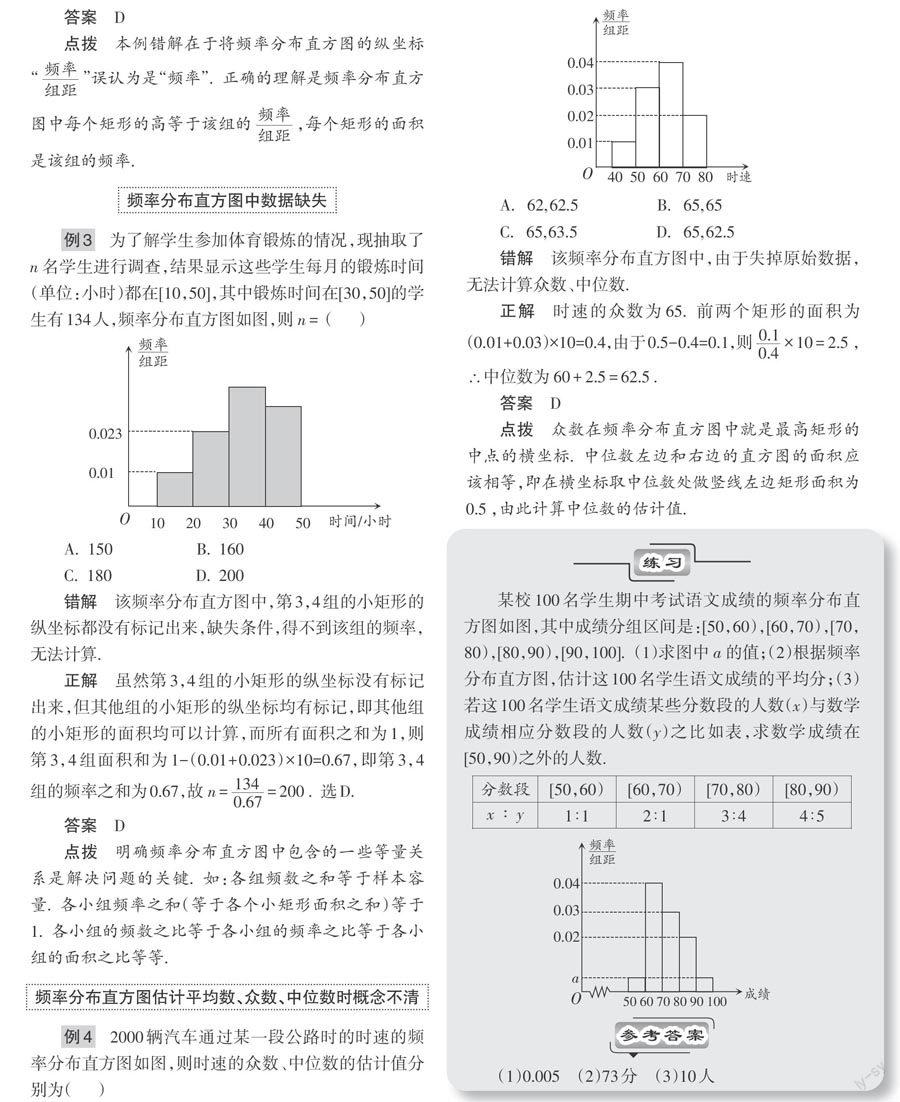
某校100名学生期中考试语文成绩的频率分布直方图如图，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]. （1）求图中的值；（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表，求数学成绩在[50，90）之外的人数.

[参考答案]

（1）0.005 （2）73分 （3）10人