一道有序集组计数赛题的求解与变式

●龚新平 (育才中学 上海 201801)

有序集组(A1，A2，…，Ak)计数问题在各类竞赛中经常出现，在刚结束的2009年上海市高中数学竞赛(新知杯)试题中就出现了一道有序集组的计数问题!本文对该问题进行了简要地分析解答，并在此基础上提出10个相关的变式问题，希望能抛砖引玉，对读者解决此类问题有所启发.

问题 设 A，B 是集合{a1，a2，a3，a4，a5}的 2个不同子集，使得A不是B的子集，B也不是的A子集，求不同的有序集组(A，B)的组数.

(2009年上海市数学竞赛试题)

解法1 由集合{a1，a2，a3，a4，a5}共有 25个不同子集知，不同的有序集组(A，B)共有25(25-1)组;若A⊂B，当集合B含k(1≤k≤5)个元素时，满足A⊂B的有序集组(A，B)共有

组，同理满足B⊂A的有序集组(A，B)也共有(35-25)组，故满足A不是B的子集且B也不是A的子集的有序集组(A，B)的组数为

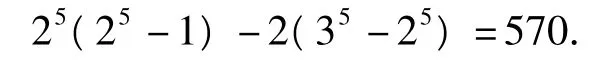
解法2 由集合{a，a，a，a，a}共有 25个

12345不同子集，不同的有序集组(A，B)共有25(25-1)组;考虑满足A⊂B的有序集组(A，B)的组数.每个元素 ai(i=1，2，3，4，5)均有 3 种归属：A，(B∩)，，故共有 35组(A，B)满足 A⊂B，排除其中A=B的25组，共有(35-25)组有序集组(A，B)满足A⊂B;同理有(35-25)组有序集组(A，B)满足B⊂A，故满足题意的有序集组(A，B)的组数为

推广 设A，B是集合{a1，a2，…，an}的2个不同子集，A不是B的子集，B也不是A的子集，则不同的有序集组(A，B)的组数为

变式1 设 A，B，C 是集合{a1，a2，…，an}的 3个不同子集，且A不是B的子集，A也不是C的子集，求不同的有序集组(A，B，C)的组数.

解由A不是(B∪C)的子集知：

变式2 设A，B是数集{a1，a2，…，an}的2个不同子集，且A中每个元素都大于B中的所有元素，求不同的有序集组(A，B)的组数.

变式3 设A，B是集合{a1，a2，…，an}的2个不同子集，且满足 A∪B={a1，a2，…，an}，求不同的有序集组(A，B)的组数.

解对于 ai=(i=1，2，…，n)有3种归属：(A∩)，(A∩B)，(∩B)，因此满足 A∪B={a1，a2，…，an}的有序集组(A，B)的组数为 3n.

变式4 若 A∪B∪C={a1，a2，…，an}，且每个 ai(i=1，2，…，n)恰好属于 A，B，C 中的2 个集合，求有序集组(A，B，C)的组数.

解对每个 ai(i=1，2，…，n)属于 A，B，C 中的某2个时有C23种归属，因此有序集组最多有3n组，但需排除A，B，C中恰有1个是φ的3种情形，故有序集组(A，B，C)的组数为(3n-3).

变式5 若 A，B，C 为集合{a1，a2，…，an}的子集，且满足 A∩B∩C=φ，A∩B≠φ，A∩C≠φ，求不同的有序集组(A，B，C)的组数.

变式6 若非空集合 A，B，C，D满足：A∪B∪C∪D={a1，a2，…，an}，且 A∩B∩C=φ，求有序集组(A，B，C，D)的组数.

解对每个 ai(i=1，2，…，n)属于 A，B，C，D最多有24=16种归属，但需排除3种情形：(1)ai不属于 A，B，C，D;(2)ai属于 A，B，C 不属于 D;(3)ai属于 A，B，C，D.故 ai有(24-3)=13 种归属，从而满足条件的(A，B，C，D)的组数为 13n.

变式7 集合 A1，A2，…，Ak是{a1，a2，…，ak}的k个子集，求满足A1∩A2∩…∩Ak=φ的不同有序集组(A1，A2，…，Ak)的组数.

解对任意元素ai∉(A1∩A2∩…∩Ak)时，共有(2k-1)种归属，故满足条件的有序集组(A1，A2，…，Ak)的组数为(2k-1)n.

变式8 设 Ai(1≤i≤k)是{a1，a2，…，ak}的 k个子集，若a1∈(A1∪A2∪…∪Ak)，求不同的有序集组(A1，A2，…，Ak)的组数.

解由{a1，a2，…an}共有2n个不同子集，故有序集组(A1，A2，…，Ak)的个数最多为 2nk个;又集合{a1，a2，…，an}的不含 a1的子集共有 2n-1个，因此不含a1的有序集组(A1，A2，…，Ak)共有2(n-1)k个，即含 a1的有序集组(A1，A2，…，Ak)共有(2nk-2(n-1)k)=(2k-1)2(n-1)k组.

变式9 设 Ai(i=1，2，…，k)是{a1，a2，…，an}的 k个不同的子集，且 A1∪A2∪…∪Ak={a1，a2，…，an}，求不同的有序集组(A1，A2，…，Ak)的组数.

解对任意元素ai∈(A1∪A2∪…∪Ak)时，共有(2k-1)种归属，于是满足条件的有序集组(A1，A2，…，Ak)的组数为(2k-1)n.

变式10 设 Ai(i=1，2，…，k)是(a1，a2，…，an)的k个不同的非空子集，且A1∪A2∪…∪Ak={a1，a2，…，Ak}，求不同的有序集组(A1，A2，…，Ak)的组数.

解对任意元素ai∈(A1∪A2∪…∪Ak)时，共有(2k-1)种归属，因此满足条件的有序集组(A1，A2，…，Ak)的组数最多为(2k-1)n;但对于有序集组(A1，A2，…，Ak)中有 i个集合为 φ 时，共有(2k-i-1)n组不符合.由容斥原理知，不同的有序集组(A1，A2，…，Ak)组数为