合理构造函数 化解教学疑难

●刘官茂 (宁波万里国际学校中学 浙江宁波 315040)

函数在高考中不仅占有较大比重，而且在新课标中也处于非常重要的地位.函数是联系代数与几何、定量与变量的桥梁和纽带，是中学数学的主干知识之一，是学好中学数学的关键.利用导数和函数的性质解决各种综合问题是高考的重点、热点和难点.本文试图通过合理构造函数化解教与学中的一些疑难问题，加强对函数本质的理解，提高函数思想的应用意识.

1 合理构造函数

1.1 根据函数性质，合理构造函数

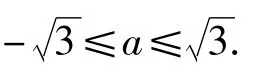
分析看到该题的第一反应是求导，利用切线与割线的斜率关系直观地阐述，或补充高等数学中的拉格朗日中值定理说明，这显然都是不合理的.要想化解这个疑难，只需设 A(x1，y1)，B(x2，y2)是函数图像上任意不同的2个点，则

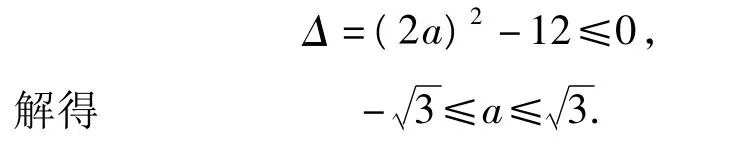
评注如果题目中涉及到曲线任意2个点的斜率范围，那么均可以按照此法来构造函数，把问题转化成函数的单调性问题，进而用导数顺利突破.解题过程清晰、自然，体现了转化化归的思想.

1.2 化定量为变量，合理构造函数

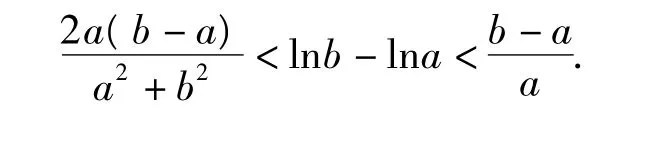
例2 当0＜a＜b时，求证：显然 x1≠x2，不妨设 x1＜ x2，则

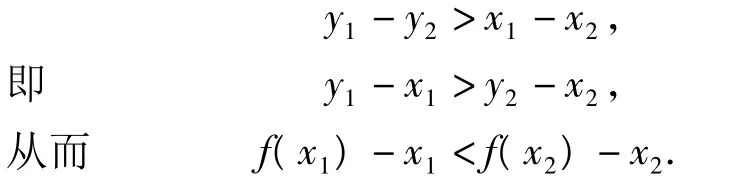
由函数的单调性可知，只需构造函数 g(x)=f(x)-x，则 g(x)在 R上是减函数，g'(x)=-3x2+2ax-1≤0在R上恒成立，故

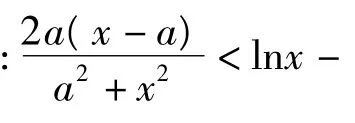
评注对于多元不等式的证明问题，可以采取这种化定量为变量，合理构造函数的方法解决.

1.3 根据消元转化，合理构造函数

例3 已知函数 f(x)=lnx，g(x)=ax2-x(a≠0)，若函数y=f(x)与y=g(x)的图像有2个不同的交点M，N，且过线段MN的中点做x轴的垂线分别与f(x)的图像和g(x)的图像交于点S，T，以S为切点作f(x)的切线l1，以T为切点作g(x)的切线l2.问是否存在实数a使得l1∥l2?如果存在，求出a的值;如果不存在，请说明理由.

分析此题入手易，深入难.设点M(x1，y1)，N(x2，y2)，由 l1∥l2可得

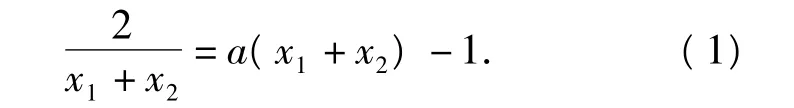
接下去，学生基本上没有思路了.通过适当消元转化则能迎刃而解.首先对式(1)两边同乘以x1-x2，得

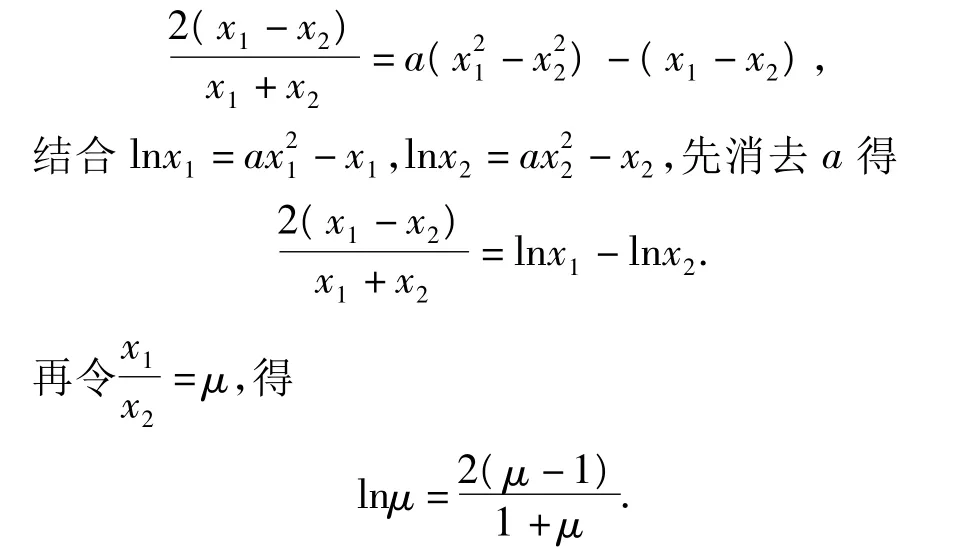
评析 此题通过2次合理消元，最后把问题蜕化为一元函数，通过求值域解决问题.对于多个变量问题，应理清变量间的关系.

2 利用函数如何化解疑难问题

2.1 利用函数性质化解疑难

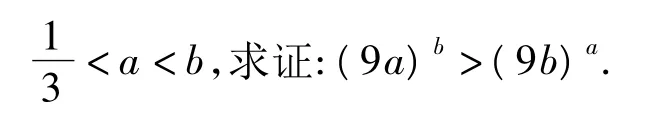
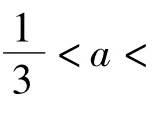
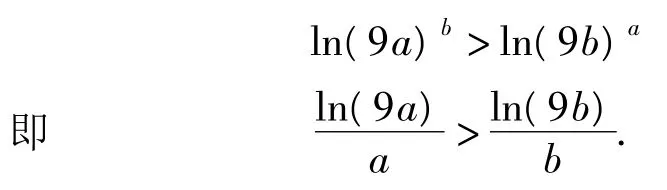
评注导数的引入后，不等式的证明多了一条出路，函数的单调性往往蕴含着大小的比较问题，合理构造函数利用单调性即可证明.

2.2 巧用数形结合化解疑难

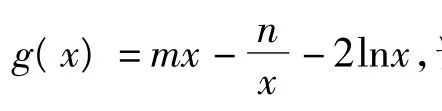
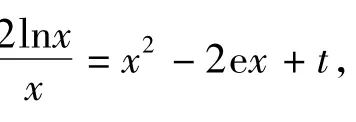
评注本题最主要的特点是对方程进行了重新“配置”，而关键点就是配置后左右2边对应的函数有相同的极值点，进而利用函数的图像分析解决问题.一般来说，对于比较复杂的方程求根或是判定函数零点的个数问题.要善于发现方程的结构特征，对方程的结构进行分离重配，转化为一边是熟悉的基本函数形式，另一边可以是较复杂的函数形式，用导数对函数的变化趋势进行研究.最后把根的个数问题转化成2个图像的交点个数问题.

2.3 妙用降维化归化解疑难

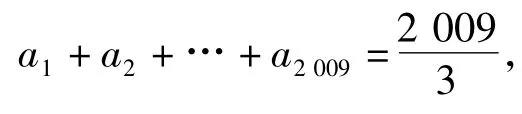
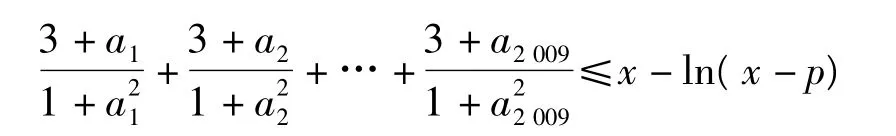
在x∈(p，+∞)时恒成立，求实数p的最小值.

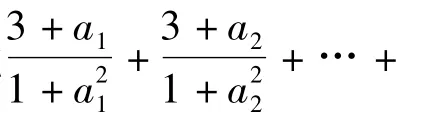
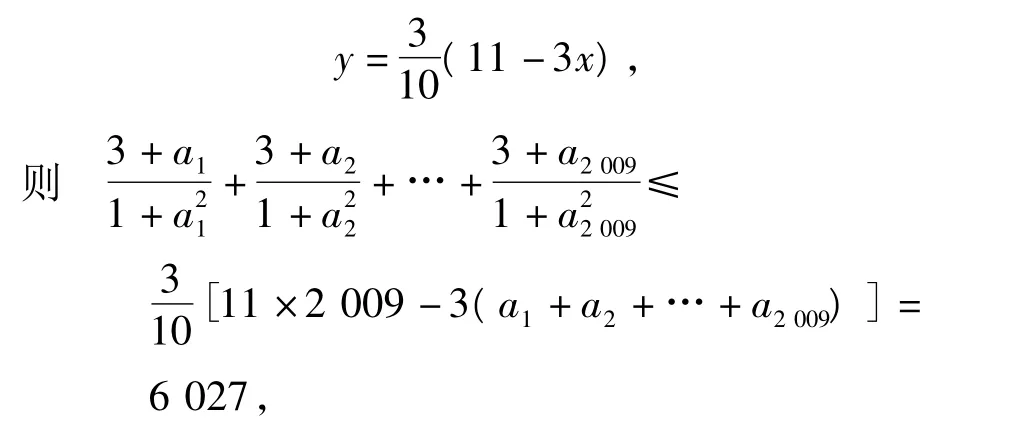
接下来，可求得x=ln(x-p)的最小值为p+1，因此 p≥6 026.

评注对于比较难化简的求和形式，一般是通过放缩或转化得到比较容易的函数形式.

在解题教学过程中，要向学生暴露思维过程，对解题切入点或突破口的选择要舍得花时间分析引导，问题解决中“坎”的跨越、“陡坡”的攀登要浓墨重彩.题目的讲评不是一味地呈现标准答案，要从学生解题“卡壳”的难点处着手突破，帮助学生解决问题，并和标准解法进行比较分析.解题后要关注反思和拓展，品味解题的方法和关键点，探索一题多解，深入理解数学本质.

难题的讲解一定要在关键点上突破，在学生的疑难点上启发，通过题组与变式的练习，强化学生的解题经验.