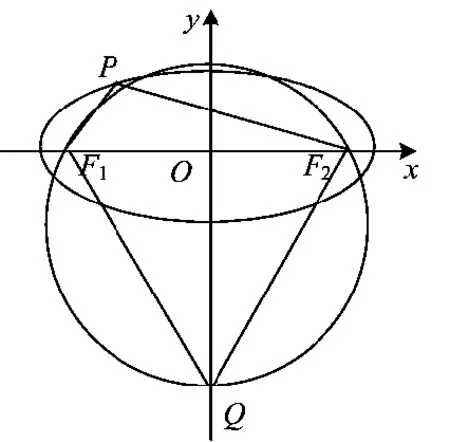
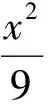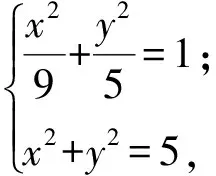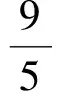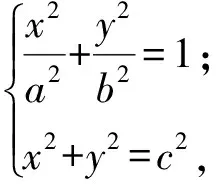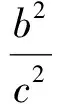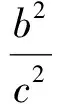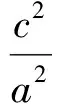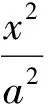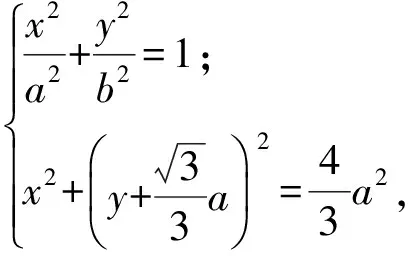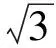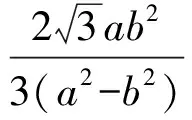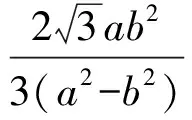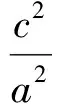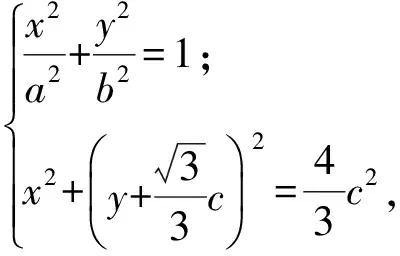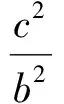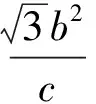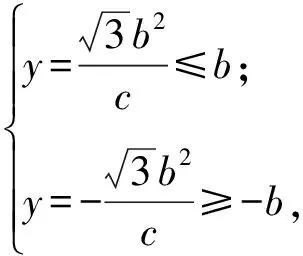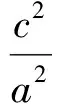巧用圆的性质解题

● (大冶市第一中学 湖北大冶 435100)

圆的性质1直径所对的圆周角是直角.

如图1所示，AB是圆的直径，P是圆周上一点，则∠APB=90°．

若P1是圆外部一点，则∠AP1B<90°，即∠AP1B是锐角；若P2是圆内部一点，则∠AP2B>90°，即∠AP2B是钝角．

利用圆的该性质可以进一步得到以下结论1．

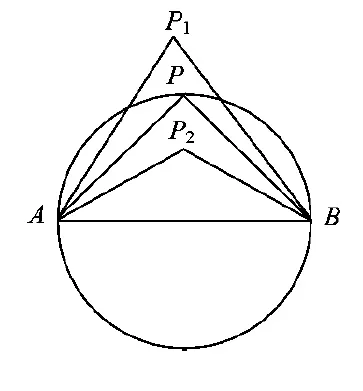
图1

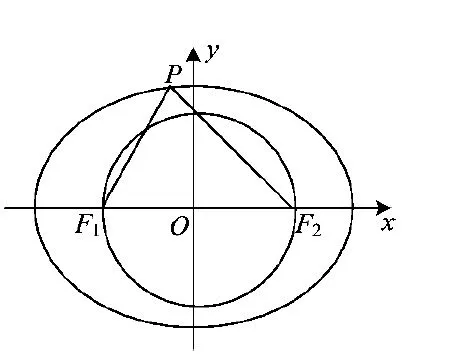
图2

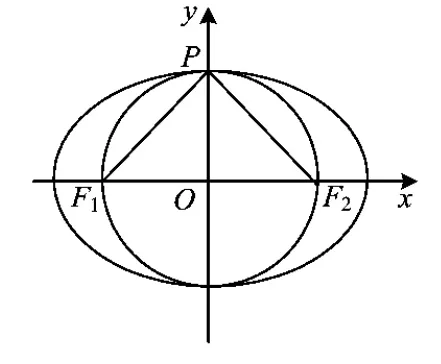
图3

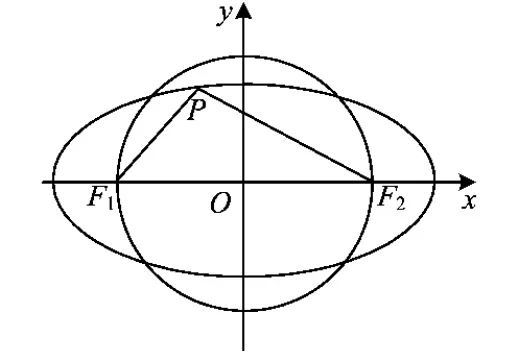
图4

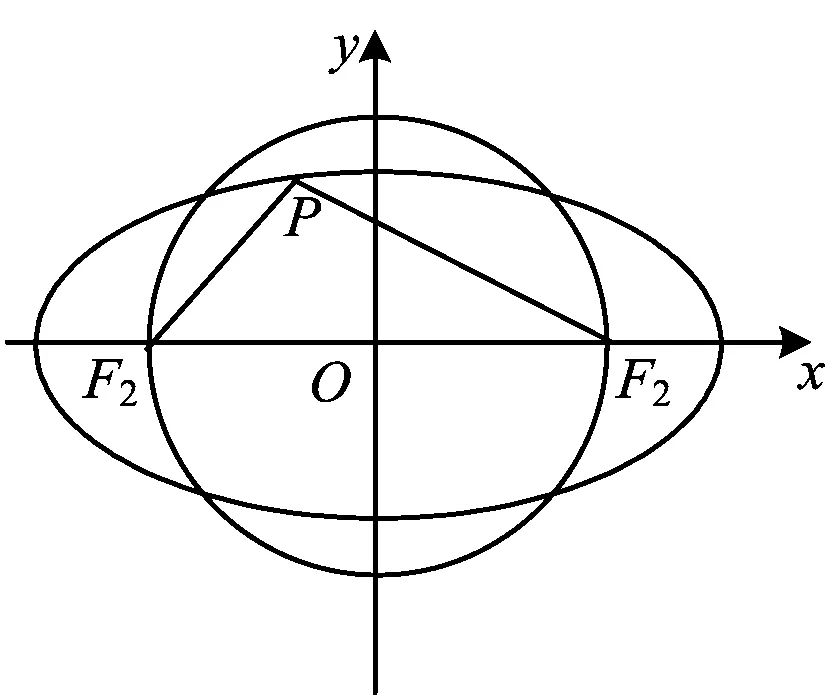
结论1以椭圆中心为圆心，以|F1F2|为直径作圆O,则圆O与椭圆的位置关系如图2～4所示．

将椭圆方程和圆O的方程联立,即

解得

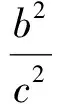
(1)当b>c时，b2>c2，则y2>b2．由图2可知，y2>b2不成立，即方程组无解．此时椭圆包含圆O，椭圆与圆O没有公共点，椭圆上的任意一点P(长轴的2个端点除外)与F1F2连线的夹角都是锐角．

(2)当b=c时，b2=c2，则y2=b2．由图3可知，椭圆与圆O有2个公共点，即短轴的2个端点．设公共点为P，则此时点P与F1,F2连线的夹角是直角,椭圆上的其余各点(长轴的2个端点除外)与F1,F2连线的夹角都是锐角．

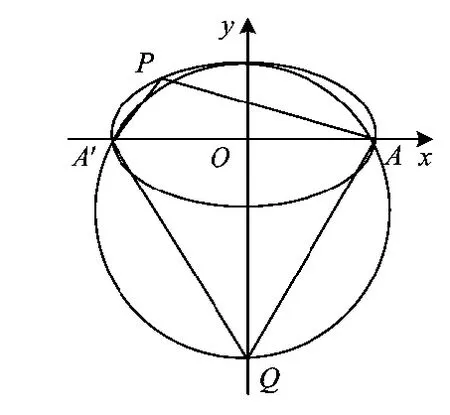
(3)当b

圆的性质2 圆内接四边形的对角互补．

本文利用圆的这些性质巧妙解题，举例加以应用，供参考.

图5

解以椭圆中心为圆心，以|F1F2|为直径作圆O,则圆O的方程为：x2+y2=c2．由上面的结论可知，要使∠F1PF2为钝角，一定有圆O和椭圆相交，即b2

解以椭圆的中心为圆心，以|F1F2|为直径作圆，记作圆O,则圆O的方程为：x2+y2=c2．联立方程组

解得

因为圆O和椭圆有公共点,得

即b2≤c2，从而

a2-c2≤c2，

所以

故

以上解法是先构造一个圆O，把∠F1PF2放到圆O中去考虑，有效地将圆的知识与解析几何联系起来；再利用圆O和椭圆的位置关系，进一步求出答案．

图6

图7

解如图6所示，以A′A为边作等边△A′QA，再作△A′QA的外接圆．由已知条件，椭圆上存在一点P，使得∠A′PA=120°,则根据圆的性质，知点P,A′,Q,A共圆，即点A是椭圆与△A′QA的外接圆的交点.将椭圆方程和△A′QA的外接圆的方程联立,得

即

解得

如图6可知，交点P的纵坐标必须满足

即

(3c2-2a2)(3c2+6a2)≥0，

得

3c2-2a2≥0,

所以

解得

例4F1,F2是椭圆的2个焦点，若椭圆上存在一点P，使∠F1PF2=120°，求椭圆离心率的取值范围．

解如图7，以F1F2为边作等边△F1QF2，再作△F1QF2的外接圆．由已知条件，椭圆上存在一点P，使得∠F1PF2=120°,根据圆的性质，知点P,F1,Q,F2共圆，即点P是椭圆与△F1QF2的外接圆的交点.将椭圆方程和△F1QF2的外接圆的方程联立,得

即

解得

如图7可知，交点P的纵坐标要满足

化简得

解得

评注从图中还可以发现，在椭圆上存在4个(或3个)不同的点，使得∠F1PF2=120°．这样就可以得到一个新的问题：

例5F1,F2是椭圆的2个焦点，若椭圆上存在4个这样的点P，使得∠F1PF2=120°，求椭圆离心率的取值范围．

例6F1,F2是椭圆的2个焦点，若椭圆上存在3个这样的点P，使得∠F1PF2=120°，求椭圆的离心率．

以上问题有一个相同的条件：已知角是120°．因此可以利用圆的性质构造一个正三角形，再作出三角形的外接圆，然后进一步确定点是三角形外接圆和椭圆的公共点；最后通过外接圆和椭圆的位置关系解出答案．