一个不等式的推广和完善

● (学军中学 浙江杭州 310012)

《数学通报》2009年第12期数学问题解答中刊登的第1 824号问题是：

笔者根据供题人给出的解法对上述不等式进行了推广，并给出了上面右边式子的一个下界.

并当a1=a2=…=an=n时，取到等号.

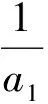
因为

所以

故当n=2时，原不等式成立.

(1)先证明左边的不等式.由柯西不等式可得

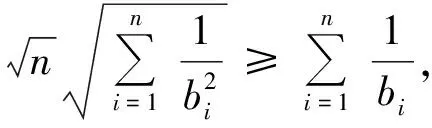
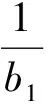
将上述n个式子相加可得

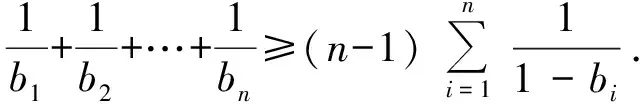
(1)

又由柯西不等式知

表5显示，随着青贮发酵时间的延长，5种不同比例混合青贮过程中大肠杆菌的数量大体呈先增加后逐渐减少的趋势，直至最后检测不出大肠杆菌的数量。0%、25%的青贮饲料中大肠杆菌数量在青贮发酵的第11 d左右达到高峰，为109数量级，50%的青贮饲料中大肠杆菌数量在青贮发酵的第20 d达到高峰，为109数量级。100%的青贮饲料中大肠杆菌数量在青贮发酵的第5 d左右达到高峰，为108数量级，到第45 d之后检测不出大肠杆菌的存在。

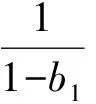
将上述n个式子相加可得到

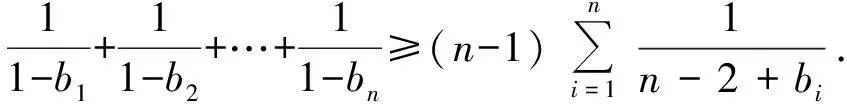
(2)

于是由式(1),式(2)可得

故

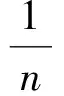
接下来证明:

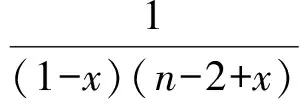
即

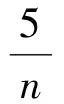
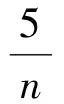
f′(x)=(nx-1)[(3n-6)x+2n-8x+9]，

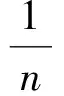
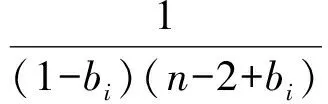
即

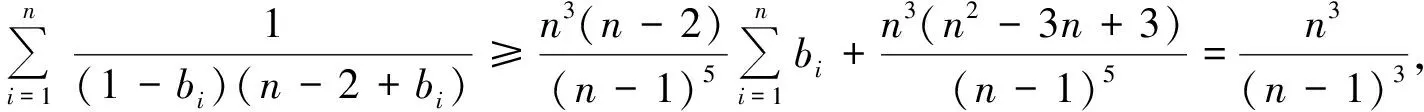
故

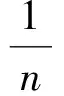
由(1),(2)可知,当n>2时，原不等式成立.