会选择恰当方法是一题多解反思后的更高境界——一道高考参数取值范围问题的解题策略比较

● (北京师范大学良乡附属中学 北京 102488)

含参函数在给定区间上单调，求参数取值范围问题，策略比较多，笔者结合2009年山东省数学高考文科试题第21题，尝试给出多种解法，探讨方法选择问题.

(1)当a,b满足什么条件时,f(x)取得极值?

(2)已知a>0,且f(x)在区间(0,1]上单调递增,试用a表示出b的取值范围.

下面仅给出第(2)小题的求解方法.

解法1使用参数分离法、均值不等式以及导数知识求b的取值范围.

由题意知f′(x)=ax2+2bx+1≥0在区间(0,1]上恒成立,即

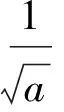
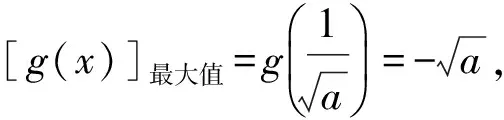
因此

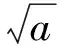
因此g(x)在(0,1]单调递增，此时

得

解法2使用参数分离法以及导数知识求b的取值范围.

由题意知f′(x)=ax2+2bx+1≥1在区间(0,1]上恒成立,即

令g′(x)=0,得

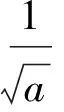
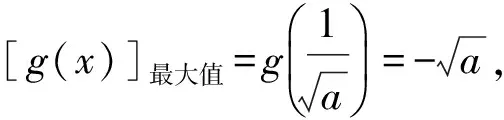
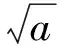
因此

解法3使用分类讨论思想以及二次函数知识求b的取值范围.

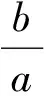
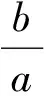
f′(x)>f′(0)=1>0，

满足f′(x)≥0在(0,1]上恒成立.因而b≥0对于一切a∈R+都能满足条件.

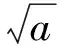
解关于b的不等式组

得

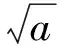
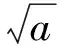
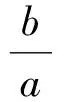
f′(x)min=f′(1)=a+2b+1≥0,

即

解关于b的不等式组

解法4使用分类讨论思想、二次函数知识以及作出平面区域的策略求b的取值范围.

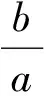
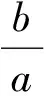
f′(x)>f′(0)=1>0，

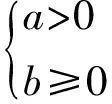
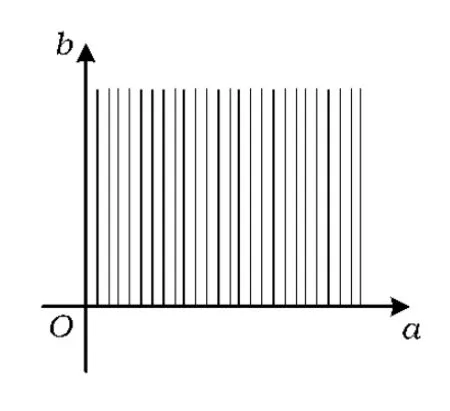
图1

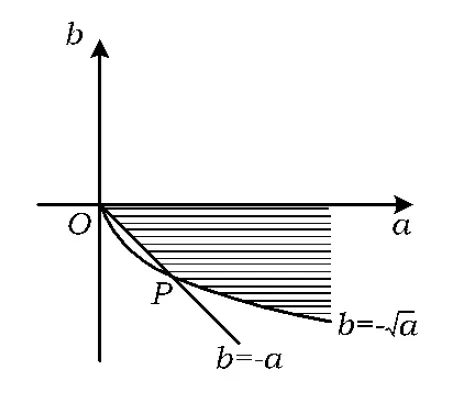
图2

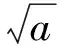
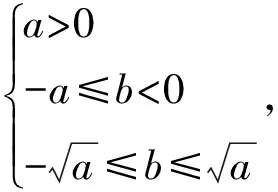
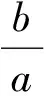
f′(x)min=f′(1)=a+2b+1≥0.

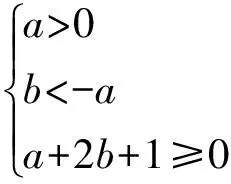
图3

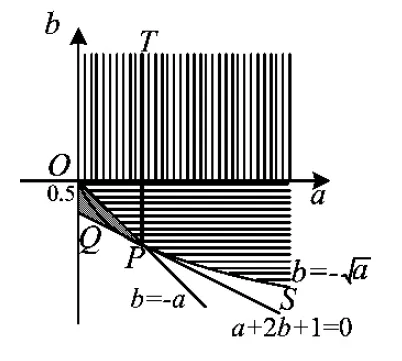
图4

综上所述：在同一个坐标系中将图1～3拼接恰好形成一个完整的阴影图形(如图4所示)，这个阴影图形是满足f(x)在区间(0,1]上单调递增的所有实数对(a,b)对应的点的集合.

下面结合该图形试用a表示出b的取值范围.

作射线PT∥b轴,则线段QP，射线PT，b轴围成的阴影区域可以表示为：

解法5用子区间法求b的取值范围.

由题意知f′(x)=ax2+2bx+1≥0在区间(0,1]上恒成立.

①当Δ≤0，即b2≤a时，不等式f′(a)=ax2+2bx+1≥0在R上恒成立，从而在(0，1]上恒成立，因此当a>0,b2≤a时,不等式恒成立,此时

②当Δ>0，即b2>a时，令f′(x)=ax2+2bx+1≥0，得

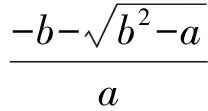
于是函数f(x)的单调增区间为

又函数f(x)在(0,1]上是增函数，从而

或

因此

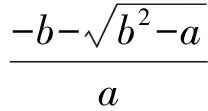
又由a>0，得

从而

解得

(2)

或

(3)

不等式组(2)可化为

即

(4)

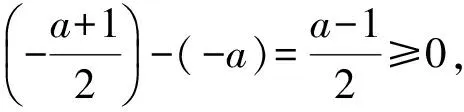
不等式组(3)可化为

即

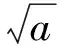
小结上述5种不同的解法分别沿着5条不同的途径得到了同一个结果.有些解法简洁，有些解法看似简单，但要经历一个漫长的过程才能达到胜利的彼岸.现对5种解法进行比较:

方法1注意到f′(x)=ax2+2bx+1≥0在区间(0,1]上恒成立,这个区间(0,1]保障了x取正值,故不等式ax2+2bx+1≥0移项后得到2bx≥-ax2-1,不等式2边同除以2x,不等式方向不改变,得到

方法1和方法2是高考参考答案提供的解法.

方法4类似于方法3,研究二次函数f′(x)=ax2+2bx+1(a>0).考虑到字母a,b同时出现在不等式或不等式组中,先同等对待字母a,b，把所得不等关系看成关于a,b的二元不等式组，用类似于线性规划研究二元不等式的作平面区域图的思想解决问题,比方法3更为直观.

方法5先求出二次不等式f′(x)=ax2+2bx+1≥0的解集，再令(0,1]为该解集的子集，比较端点值得到关于b的不等式.看似思路简单,但操作难度不小,选择此法势必要遭遇解无理不等式带来的荆棘.

综上所述,方法1和方法2体现了问题解决的简洁性和可行性；方法2反映了学生思维的习惯性，但需要问题思考的缜密性；方法3体现了思维的灵活性和对问题理解的深刻性；方法4体现了数形结合的思想，从图形上对所得答案进行了诠释；方法5体现了问题解决的程序性，但需要有解决无理不等式的熟练技巧.