一道IMO试题的证明与推广

● (潜山中学 安徽潜山 246300)

第49届IMO比赛于2008年7月中旬在西班牙首都马德里举行，其中第1天的第二大题中的第(1)小题是一道不等式证明题，现摘录如下：

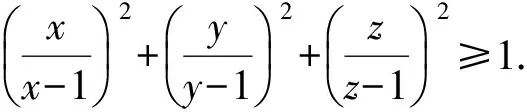
分析这是一道形式简洁、结构优美、令人无限遐想的代数不等式证明题，引起了笔者极大的兴趣与思考，并对该题作了深入探究得到问题推广的一般性结论．

1 问题的证明

证明设x-1=a,y-1=b,z-1=c(abc≠0),则

x=a+1,y=b+1,z=c+1.

由题意得

xyz=(a+1)(b+1)(c+1)=1,

于是

abc+ab+bc+ac+a+b+c=0.

(1)

式(1)两边同除以abc,并整理得

在式(2)两边平方并整理得

因此

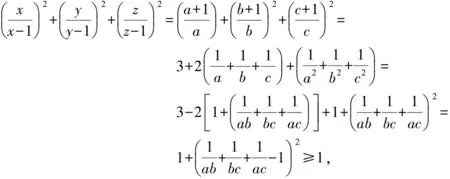
即

2 问题的推广

推广1设实数x,y,z都不等于1,满足xyz=1,λ,μ∈R，则

证明设x-1=a,y-1=b,z-1=c,则abc≠0，从而x=a+1,y=b+1,z=c+1,仿前可得式(1)，(2)，(3).于是

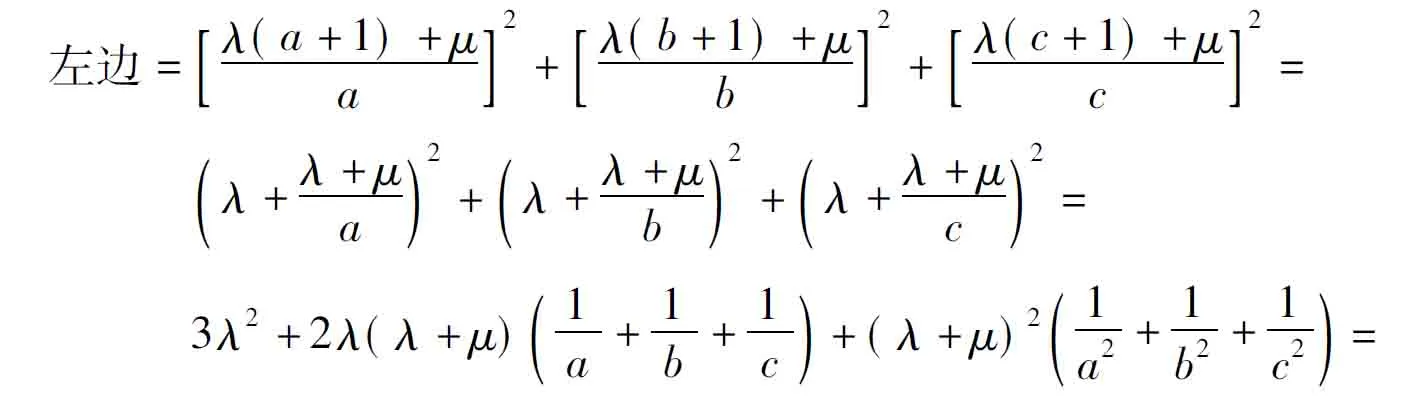
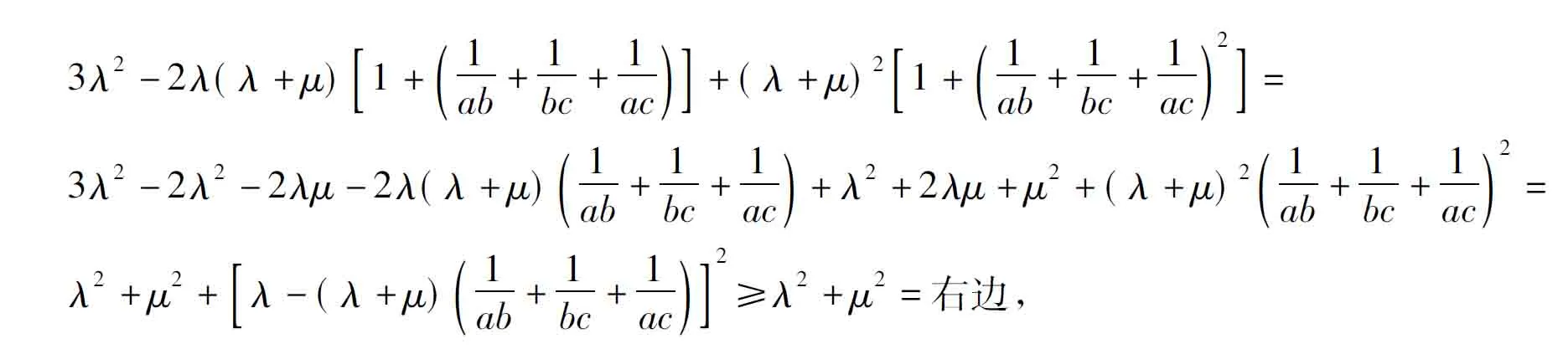
即

推广2设实数a,b,c互不相等且abc≠0,λ,μ∈R，则

若在不等式(5)中，令λ=2,μ=-1便可得2004年泰国的一道奥林匹克竞赛题：

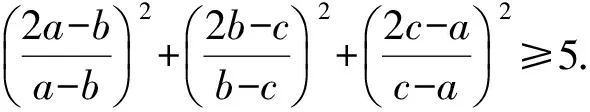
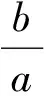
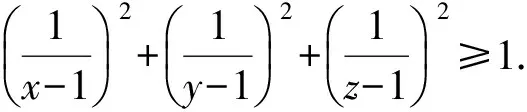
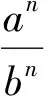
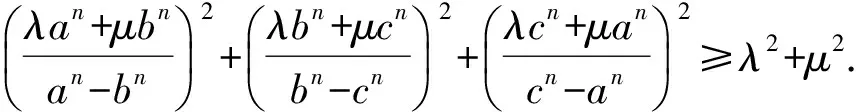
(6)

在式(6)中,根据需要可取λ,μ,n为恰当的值,便能由此得到一系列的不等式.

推广4设实数x,y,z都不等于k,且xyz=k3(k≠0)，则

证明设x-k=a，y-k=b,z-k=c(abc≠0),则

xyz=(a+k)(b+k)(c+k)=abc+k(ab+bc+ac)+k2(a+b+c)+k3=k3，

因此

abc+k(ab+bc+ac)+k2(a+b+c)=0.

于是

则

从而

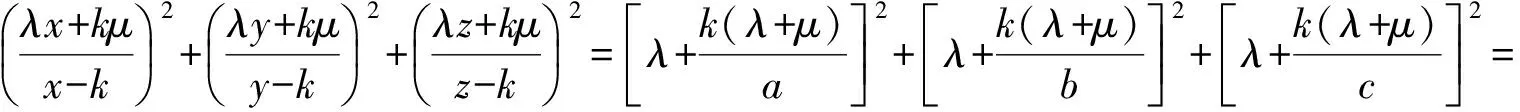
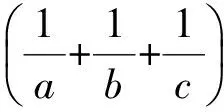
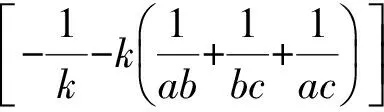
故