从著名的外森比克不等式引发的思考

● (咸阳师范学院基础教育课程研究中心 陕西咸阳 712000)

1919年，数学家外森比克(Weitzenböck)提出了如下三角形边长和面积的一个优美不等式：

问题1设△ABC的3条边长为a,b,c，面积为Δ，则有不等式

此题曾经作为1961年国际数学竞赛题.围绕不等式(1)有许多有趣的加强和拓广.我们知道，早就有加强(1)的Tsintsifas不等式[1]：

问题2设△ABC的3条边长为a,b,c，面积为Δ，则有不等式

问题3设△ABC的3条边长为a,b,c，面积为Δ，则有不等式

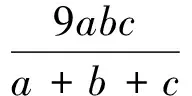
在文献[2]中，作者将不等式(2)变形为：

问题4设△ABC的3条边长为a,b,c，其半周长和面积分别为p,Δ，则有不等式

值得一提的是:1937年，数学家费恩斯列尔(Finsler)——哈德维格尔(Hadwiger)将不等式(1)加强为如下不等式：

问题5设△ABC的3条边长为a,b,c，面积为Δ，则有不等式

这个不等式还可以等价变形为：

等价于

事实上，用不等式(3)来证明不等式(5)是非常简单的，请看：

证明由三元均值不等式和不等式(3)，得

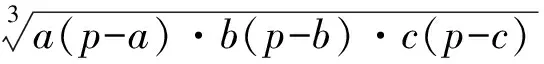
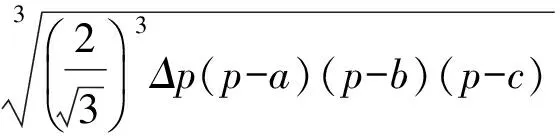
获证.

早在1982年，重庆市第二十三中学高灵教师将不等式(4)推广为2个三角形的情形：

问题6设△ABC和△A′B′C′的3条边长分别为a，b，c;a′,b′,c′,其面积分别为Δ和Δ′，则有不等式

下面给出一个比较简单的证法.

H2=[a′(b+c-a)+b′(c+a-b)+c′(a+b-c)][a(b′+c′-a′)+b(c′+a′-b′)+c(a′+b′-c′)]=

4[a′(p-a)+b′(p-b)+c′(p-c)][a(p′-a′)+b(p′-b′)+c(p′-c′)]≥

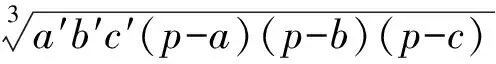
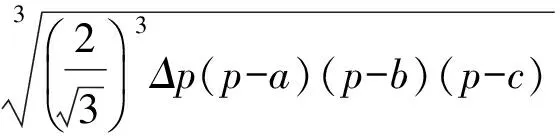
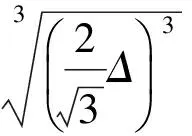
事实上，不等式(5)还可以推广到多个三角形的情景(见文献[2]).

问题7设△AiBiCi的边长、半周长和面积分别为ai,bi,ci,pi,Δi(i=1,2,…,n)，则有

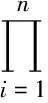
还需要指出的是，不等式(2)还可以继续加强，得到如下的不等式：

问题8设△ABC的3条边长为a,b,c，面积为Δ，则有不等式

证明由射影定理，得

a=bcosC+ccosB．

于是应用著名的柯西不等式，得

a2=(bcosC+ccosB)2≤(b2+c2)(cos2C+cos2B)，

即

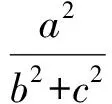
变形得

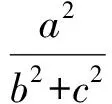
同理可得

将这3个不等式2边相加，便得

注意到常见的不等式

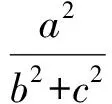
可得

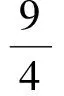
再结合正弦定理，可得

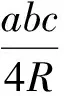
变形得

即

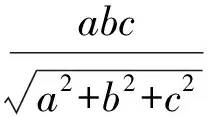
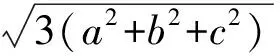
(本文获咸阳师范学院重点科研课题(08XSYK110)、陕西省教育科学“十一五”规划(SGH090228)项目支持.)

[1] 苗兴振，董林.Weitzenböck及Tsintsifas不等式的加强[J].中学数学月刊，2010(2)：45.

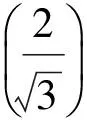
[3] 安振平.以三正数为边长可构成三角形的充要条件及应用[J].湖南数学通讯，1985(3):17-19.