构造辅助数列解决一些有关自然数的问题

● (兰州市第六十六中学 甘肃兰州 730050)

在处理一些有关自然数的问题时,根据题目提供的信息,通过联想,恰当地构造一个有助于解题的辅助数列,从而达到解题的目的,是一种很有用的解题方法.现举例说明之.

1 证明等式

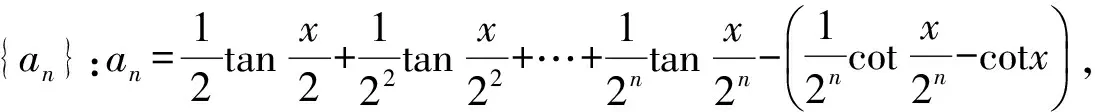
因为

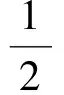
所以

a1=a2=…=an-1=an=0,

故原等式得证．

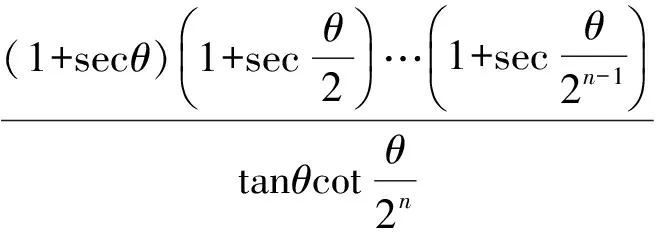
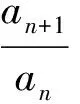
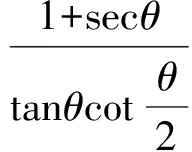
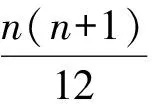
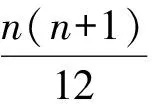
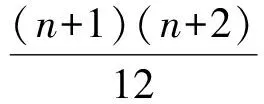
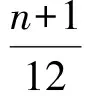
令3-a=0,48-5a-3b=0,24-a-b-c=0,解得a=3,b=11,c=10,此时

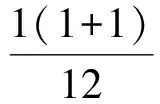
故存在常数a=3,b=11,c=10,使得an=an-1=…=a1=0,即原命题成立.

2 证明不等式

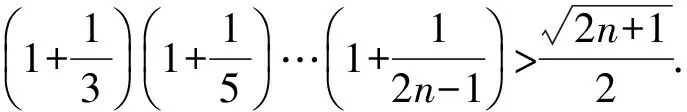
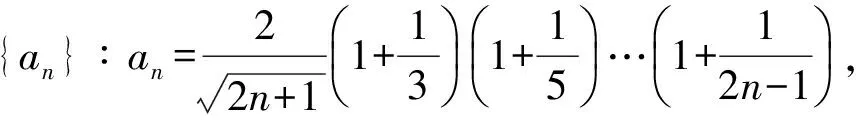
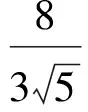
an>an-1>…>a2>1，

故原不等式得证.

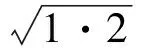
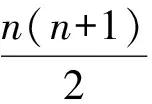
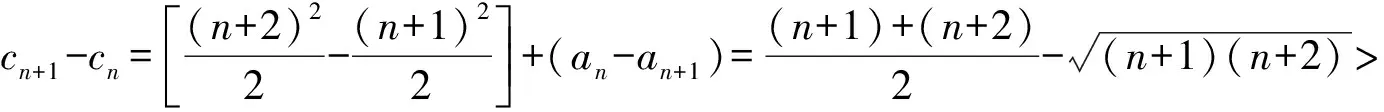
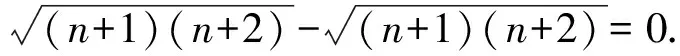
bn>bn-1>…>b1>0,cn>cn-1>…>c1>0,

故原不等式得证.

3 求数列的通项

对一些直接求解有困难的数列通项问题，若能适当变换，构造一个等差或等比数列，则原问题可以通过后者的“桥梁”作用顺利解决.

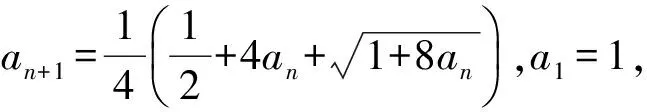
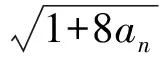
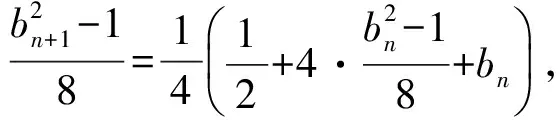
即

由bn>0,得bn+1-bn=1,因此{bn}是以1为公差，以3为首项的等差数列，于是

bn=3+(n-1)·1=n+2,

故

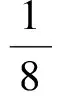
例7已知数列{an}和{bn}满足：a1=p,b1=q,且an=pan-1,bn=qan-1+rbn-1(n≥2),其中q≠0,p>r>0,试求数列{bn}的通项.

解显然an=pn,得bn=qpn-1+rbn-1,即

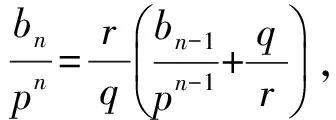
两边同时加常数α,则有

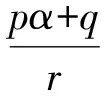
故

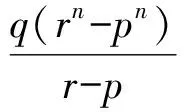
4 研究数的整除性

对一些有困难的数的整除问题，若能适当变换，构造一个辅助数列，则原问题可以通过后者的“桥梁”作用顺利得以解决.

an=28an-1-16an-2(n≥3).

由a1=22×7,a2=23×94,知当n=1,2时成立.

例9试证:11n+2+122n+1(n=0,1,2,…)能被133整除.

证明构造辅助数列{an}:an=11n+2+122n+1=121·11n+12·144n.由11，144是方程x2-125x+1 584=0,即xn=125xn-1-1 584xn-2的根，可将x=11,x=144代入并将所得式子相加得

an=125an-1-1 584an-2(n≥2).

又由a0=133,a1=3 059=133×23均能被133整除,递推可知，an=11n+2+122n+1能被133整除.

5 解应用题

在处理一些与自然数有关的应用题时，可以先构造一个辅助数列，然后寻找并建立递推关系，再根据递推关系，确定相应的若干个初始值，最后通过对该数列性质的研究而使原问题得到解决.

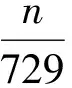
(第3届美国数学邀请赛试题)

解设ak为小虫从点A出发后第k步(每步1米)能回到点A的走法总数，则有a1=0，小虫从点A出发，每走一步都有3种走法，于是走k-1(k≥2)步就有3k-1种走法.这些走法可分为2类：

(1)第k-1已到达点A，这类走法有ak-1种；

(2)第k-1步不在点A，这时再爬行一步(第k步)只能以唯一方式到达点A，因此这类方法有ak种，故

ak+ak-1=3k-1,

即

ak=-ak-1+3k-1.

两边同时加上α·3k得

ak+α·3k=-[ak-1-(3α+1)3k-1].

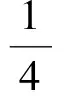
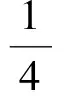
故小虫第k步回到点A的概率是

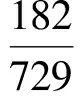
从以上诸例可以看出，构造辅助数列解题，其思维具有独创性，方法具有独特性，而且简捷巧妙，能收到事半功倍之效，这对于提高学生的解题技能、培养和发展学生的创造性思维具有重要作用.