基于有限元分析的铝合金轮毂结构优化设计

（厦门民兴工业有限公司，福建 厦门 361006）

【摘 要】轮毂是汽车重要的安全部件。文章对有限元分析软件进行二次开发，推算并绘制适合A356-T6铝合金轮毂的零件S-N曲线。运用Simulation软件，以轮毂径向冲击测试为例，建立有限元分析力学模型，分析轮毂冲击的静态影响因素和动态冲击载荷下的最大应力。基于有限元分析，对轮毂进行优化前后强度的分析比较。依据零件S-N曲线，先行预测轮毂强度状况，从而为铝合金轮毂的结构设计与优化提供方法和方向。

【關键词】轮毂；二次开发；有限元；S-N曲线；径向冲击；优化

【中图分类号】U463.343 【文献标识码】A 【文章编号】1674-0688（2016）07-0059-05

1 概况

随着社会的发展，汽车已经成为家庭的代步工具，汽车零部件的强度分析对于汽车的安全性能尤为关键。汽车轮毂作为汽车重要的安全部件，其强度分析是设计过程中必须考虑的重要因素。随着汽车市场竞争的加剧，“质量轻、强度高、美观性强”已经成为现代汽车制造业的主要设计理念，因此在汽车轮毂的初期设计中要体现此设计理念。由于轮毂工作在随机载荷之下，在其研制中最关心的问题之一就是轮毂的抗径向冲击能力，在铝合金轮毂的设计开发，抗径向冲击能力是比较贴近实际行驶路况的测试。因此，如何在设计中优化其结构设计，以减少轮毂开模后在实际试作中的次数和避免强度改善的盲目性，其初期的结构设计和结构优化非常重要。

本文主要阐述如何利用基于Simulation有限元分析软件来辅助、优化、改善轮毂的结构设计，以寻求到强度高、轻量化的结构设计。首先计算并绘制A356-T6铝合金轮毂的S-N曲线，并对软件进行二次开发，然后将S-N曲线写入软件材质库，对铝合金轮毂进行静应力分析，再通过S-N曲线，寻找满足疲劳寿命下所对应的最大应力值。本文主要讨论铝合金轮毂的冲击应力的有限元力学模型，并与实际生产结果比对，验证其合理性，以对铝合金轮毂后续的有限元分析提供方向。

2 轮毂有限元分析及二次开发

2.1 有限元分析及二次开发的意义

目前，国内中小型的铝合金轮毂企业，设计人员判断轮毂结构强度主要是基于直觉的准则法，依靠经验数据的积累和参考类似结构的产品，即产品的开发设计水平主要取决于设计人员的实际经验和对这些方法的把握能力。设计轮毂结构时，都很少进行结构优化，轮毂的强度全凭经验设计，强度问题只能在试作过程中测试试验发现，再根据实际测试结果去改善强度，不仅浪费了生产成本，也拉长了产品的开发周期，延后产品上市时间。

随着市场的发展和竞争的加剧，客户对轮毂的可靠性和经济性要求不断提高，故需要改进新产品开发流程，提高研发水平和开发设计能力。有限元分析的介入，在产品设计初期就可以对轮毂强度进行仿真，预先发现潜在的问题，并为结构的改善提供了优化方向，增加量产品的可靠性，避免在产品试作过程中的成本和时间的浪费，也可在保证安全可靠的前提下，优化结构，节省不必要的材料，使轮毂达到“高强度、轻量化”的目的。

在有限元分析的基础上的二次开发技术也很重要，它使有限元分析工作一目了然，操作方便快捷，节省操作环节中不必要的时间浪费。

2.2 S-N曲线的二次开发

以材料标准样件的疲劳强度为Y轴，以疲劳寿命为X轴，表示一定循环特征下标准样件的疲劳强度与疲劳寿命之间关系的曲线，成为应力-寿命曲线，也称S-N曲线。材料的S-N曲线是指把原材料做成圆棒形，在制定的加工精度等级和热处理工艺下的标准样件，得到相应的S-N曲线。因此，不同零件、不同形状、不同加工精度和热处理工艺，其S-N曲线也自然不同。

Simulation软件里面只有材料的S-N曲线，利用该曲线对铝合金轮毂进行有限元分析，模拟的结果会与实际产品的测试结果差距甚远，对实际生产没有指导意义。只有计算并绘制出与轮毂实际测试状况接近的零件S-N曲线，有限元分析才对产品设计有指导意义。目前，铝合金轮毂主要使用的材料是A356-T6。该材料的一些机械性能及相对比见表1。

σa /σNf+σm /Su=1（1）

公式（1）中，σa为交变应力作用下的平均应力；σNf为完全加载扭力的交变应力；σm为平均应力；Su为强度极限。

根据表1的材料属性，可以使用公式（1）计算出材料的疲劳寿命。

σ'Nf=σ'f×（2Nf）b（2）

σmax×εa×E=（σ'f）2（2Nf）2b+σ'f ε'f E（2Nf）b+c（3）

σmax=σa+σm

作为铝合金轮毂，主要材料为AT356-T6。轮毂主要承受静态疲劳、动态疲劳、瞬间疲劳，使用修正Goodman图，S-N曲线的修正公式如下：

σa=（Su-σm）×（2Nf）b

σmax=1 822×Nf∧（-0.201）

利用公式，求解出各个节点上的应力值，并绘制出适用于A356-T6为材料的铝合金轮毂零件的S-N曲线（如图1所示）。

利用公式，可以直接计算出产品在满足某个疲劳寿命下的最大应力值。这样可以大大简化有限元分析工作，可以不需要模拟在该最大应力下的寿命周期。依照不同的测试标准，对应不同的应力值（见表2）。

很多有限元分析模型以材料的降伏强度来判定冲击模拟是否成功，其模拟结果与实际冲击试验往往差距甚远，对现实的生产没有指导意义。而由材料S-N曲线推算修正后的零件S-N曲线对应计算出的应力值作为有限元分析的判定基准，与实际测试比较吻合，可为零件的结构优化和强度改善提供方向。

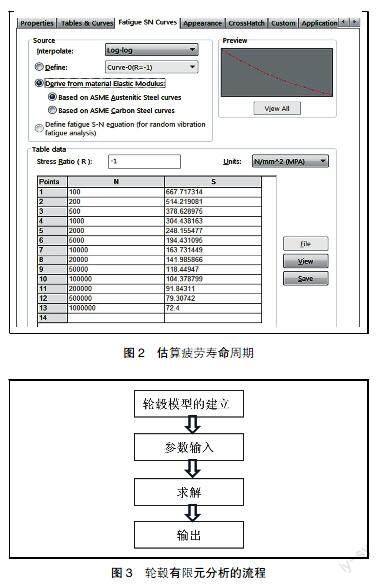
在Simulation有限元分析软件中写入每个点对应参数，绘制出相应的S-N曲线，可以较准确地估算疲劳寿命周期（如图2所示）。

3 基于有限元分析的结构优化

本文主要以22×10.5J+55 5/120MAXLOAD：815 kg为例，以轮毂13度冲击试验作为冲击强度计算，承受瞬间疲劳的有限元模型，来讨论基于有限元分析的结构优化。

3.1 轮毂有限元分析的流程

轮毂有限元分析的流程如图3所示。

3.2 13度冲击测试有限元模型

13度冲击试验是为模拟实际行驶过程中遭遇来自侧面撞击的情况，如石头或者马路牙子。轮毂主要承受瞬间疲劳。

冲击试验机上有一个从冲击面至少125 mm宽、375 mm长的垂直动作的重锤。将轮毂装胎、充气后，安装在试验机上，使轮毂的中心轴线与垂直方向为13°±1°角，其最高点面对重锤。保证重锤在轮毂正上方，并与轮毂重叠25 mm，将重锤提到高于轮毂最上方230 mm处，然后将其释放，让冲头落下冲击轮毂轮胎总成。

如果试验中轮辐在任意断面处有可见性或探伤后大于5 mm裂痕，轮辐从轮辋上分离或者轮胎内空气在1 min内漏10%以上等现象，就认为试验失效。如果被重锤面板冲击的轮截面处出现裂痕但是轮胎没有漏气，则不能认为试验失效。冲击测试试验机如图4所示。

13度冲击测试有限元分析模型要进行2次分析。分析#1主要是计算冲击的静态影响因素。冲击重锤是从一定高度落下的，因此，还要建立一个分析#2，分析动态冲击下的最大应力水平。

3.2.1 建立算例

（1）冲击的主要力量来源为重锤。重锤质量与轮毂的最大载荷有关。

重锤质量的计算公式：

W=0.6×W1+180

公式中，W为重锤质量（kg）；W1为最大荷重（kg）。

W=0.6×815+180=669 kg

（2）模型处理。从轮毂耳部外径向中心偏移1 inch，切割出轮毂上受重锤冲击的受力面，一般为2个曲面；再旋转轮毂，使轮毂的中心轴线与垂直方向为13°，划分出来的受力面迎接重锤的垂直冲击。

（3）模型材质赋予。为模型添加材质为A356-T6，其弹性模量为72.4×103 MPa，泊松比为0.33，密度为2.67×103 kg/m3，T6后硬度为75HB，最终成品硬度为90 HB。

（4）设定约束。设定5个P.C.D.螺丝孔为固定，限定X轴转动、Y轴转动、Z轴转动、X轴移动、Y轴移动5个自由度。设定安装面相对于夹具接触面的垂直位移为0，限定Z轴移动。这样就限定了6个自由度，为完全定位。

3.2.2 定义载荷

輪毂冲击时，要先安装轮胎，并对轮胎充气后，安装在试验机上，调整好重锤质量和重锤高度，再启动开关，让重锤垂直落下，撞击轮毂。

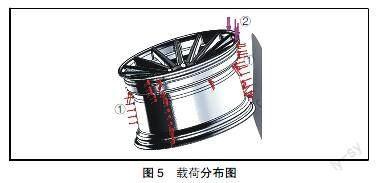
（1）模拟实际冲击，充气压力为29 psi，即轮辋面上受到29 psi的压力，如图5的箭头①所示。

（2）对分割出来的受力面，施加669 kg的重锤质量，如图5的箭头②所示。

3.2.3 静态分析属性设置

这个步骤对于冲击分析来说是非常重要的一个步骤。因为分析#1主要是要计算静态影响因素，即冲击位置的变形量，所以在“静态分析属性设置”里，选择“大位移”，求解器选择“自动求解器”（如图6所示）。

3.2.4 划分网格

在轮毂的有限元分析工作中，网格划分的原则是在确保计算精度的前提下，尽量减少网格数量，提高有限元分析的效率。直观上看，网格各内角或各个边相差不大、网格面不过分扭曲、边节点位于边界等分点附近，这种网格质量较好。

由于轮毂属旋转体，故对此轮毂采用基于曲率的网格，经过多次网格划分和计算，最终确定最大单元格为8 mm，最小单元格为1.6 mm，网格如图7所示。

3.2.5 有限元模型计算结果分析#1

查看分析结果的最大Iso修剪，可以得出静态影响因素εs=0.042 inch。即，轮毂受到重锤冲击后，冲击位置的最大变形量为0.042 inch（如图8所示）。

3.2.6 计算冲击高度影响因素

冲击试验有2个重要因素：一是冲击重锤质量；二是重锤落下高度，即冲击高度。

冲击的高度影响因素n的计算公式如下：

n=1+2×（H/εs）^0.5

上式中，n为冲击高度影响因素；H为冲击高度（in）；s为静态影响因素（in）。

计算出n=1+2×{（230/25.4）/0.042}^0.5=22.18。

3.2.7 计算动态冲击载荷Li

动态冲击载荷，即模拟重锤由一定高度落下，砸到轮毂上，对轮毂施加的载荷。

动态冲击载荷Li的计算公式如下：

Li=W×n×Af

上式中，W为重锤质量；n为冲击高度影响因素；Af为吸收因素，是一个因轮胎、安装夹具等减少冲击力的一个经验常数，取0.152。

计算得出：Li=669×22.18×0.152=2 256 kg。

3.2.8 有限元模型计算结果分析#2

返回“定义载荷”模型，将载荷修正为2 256 kg，计算冲击应力。经有限元分析模型，分析得出其应力值，最大应力的位置及大小如图9所示：最大应力274.1 MPa>冲击极限应力230 MPa，判定为冲击不合格。而此款轮毂的实际测试不合格照片如图10所示，也是在轮辋与耳部交接处撕裂，与模拟结果相符。

3.3 结构优化方案

针对轮辋与窗口交接处应力大，判定为此处强度较弱，优化方案如下：将耳部厚度由6 mm增厚到7.5 mm，并将轮辐与耳部交接处R角由R2改大至R4。优化前后3D造型对比如图11、图12所示。

（1）重新进行有限元模型分析，分析结果#1，得出静态影响因素：εs=0.081 9。

（2）计算出冲击的高度影响因素：n=1+2×{（230/

25.4）/0.0819}^0.5=15.86。

（3）计算动态冲击载荷：Li=669×15.86×0.152=

1 613 kg。

（4）返回“定义载荷”模型，将载荷修正为1 613 kg，得出分析结果#2。经有限元分析模型，分析得出其应力值，最大应力的位置及大小如图13所示。

最大应力200.7 MPa<冲击极限应力230 MPa，判定为冲击合格。

实际生产中，依此方案修改，其测试结果（如图14所示）也较佳。

4 结语

本文以A356-T6铝合金轮毂为研究对象，推算适合铝合金轮毂零件的S-N曲线，并以有限元分析软件为辅助工具，尽力轮毂力学模型，对轮毂进行冲径向冲击应力有限元结构强度分析，找到轮毂强度的改善方向和优化轮毂结构思路，以减少轮毂开模后試做的次数和避免强度改善的盲目性，使新产品实际的开发过程节约更多的时间与成本，增强企业的竞争力，为客户的新品上市赢得时间。

参 考 文 献

[1]Mehadad Zoroufi & Ali FAtemi.Fatigue Life Compar-isons of Competing Manufacturing Processes：A Study of Steering Knuckle[J].The University of Toledo，2004（1）.

[2]郦明.汽车结构抗疲劳设计[M].合肥：中国科学技术大学出版社，1995.

[3]徐灏.疲劳强度设计[M].北京：机械工业出版社1981.

[4]程育仁，缪龙秀，侯炳麟.疲劳强度[M].北京：中国铁道出版社，1990.

[5]王渭新，张磊，刘智冲.有限元分析在轮毂设计中的应用[J].现代制造技术与装备，2007（4）.

[6]李平化，周华祥，龙华.铝车轮设计的有限元分析[J].装备制造技术，2006（6）.

[责任编辑：钟声贤]

【作者简介】刘银峰，男，福建安溪人，本科，厦门民兴工业有限公司工程师，研究方向：铝合金轮毂有限元模型。