基于SP-ABC算法的数控铣削参数优化*
(江苏信息职业技术学院,无锡 214153)
随着制造业的不断发展,数控加工技术已成为现今机械制造行业生产加工的主流,数控加工的主要目的是提高生产效率、缩短加工时间和节约加工成本。而这些目标的实现都与切削参数的合理选择有着密不可分的关系,在这种情况下就引出了一个优化问题,即在给定的加工约束条件下,如何合理地选择出一个最优的切削参数组合以实现上述的优化目标。
目前,针对切削参数优化问题,国内外已有很多学者对其进行了研究。北京航空航天大学的陈志同等[1]提出了以单位时间利润率为目标函数的单元切削过程的切削参数优化模型。重庆大学的李聪波等[2]提出了面向高效低碳的数控加工参数多目标优化模型。北京航空航天大学的张青等[3]在约束处理方法上引入了非固定多段映射罚函数法和半可行域的概念,并应用于粒子群算法实现了切削参数优化。李新鹏等[4]在基本粒子群算法的基础上,引入邻居的概念,提出了一种元胞粒子群算法对切削参数进行优化。华中科技大学的陈志楚等[5]以最大化生产率为目标,运用帝国主义竞争算法对切削参数优化进行了研究。从以上的现有研究状况可以看出,虽然目前的研究都是对加工效率、加工成本等目标进行优化,但大多数仅针对单一的工序或单次走刀的切削问题来优化求解,他们没有考虑到切削加工过程是多道工序组合切削的特点。因此,这些研究虽然对单道工序或单次走刀问题具有一定的优化效果,但对整个切削加工过程而言,优化效果并不十分明显。基于此,本文以铣削加工为例,充分考虑铣削过程是多道工序组合加工这一特点,通过改进的人工蜂群算法,可同时对多道工序的切削参数同步进行优化,大大提高整体切削过程的加工效率。
1 切削参数优化模型
切削参数优化模型主要包含3方面内容:优化变量、目标函数、约束条件[6]。
1.1 优化变量
以铣削加工为例,一个完整的铣削加工过程应包含多道粗铣加工及一道精铣加工,其所具有的待优化切削参数变量包括,粗切削速度vri(i=1,2…,n),粗每齿进给量fri(i=1,2…,n),粗切削深度dri(i=1,2…,n),粗加工次数n,精切削速度vs,精每齿进给量fs,精切削深度ds等。其中,(d为总切削余量)。
1.2 目标函数
在生产中,企业最主要的目的就是追求利润,而追求利润最直接的体现就是控制生产成本,因此本文以最低加工成本作为优化目标函数。
不考虑工件材料成本的前提下,铣削加工过程中的生产成本UC包括实际进行切削加工的成本Cm,换刀操作成本Ch,工件装卸及刀具空走所需成本CR,刀具磨损成本CT。则有:

式中:ko为单位时间人工成本和管理成本之和,D为刀具直径,L为切削长度,Z为铣刀齿数,To为工序辅助时间,h1、h2为车刀空走时间和进退刀时间有关的常量,te为换刀时间,kt为刀刃成本。铣削加工刀具寿命为

式中:Cv为刀具耐用度系数,α、β、γ分别为v、f、ap对刀具寿命的影响指数,v、f、ap为切削速度、进给量、切削深度。
1.3 约束条件
实际加工中,切削参数的选择涉及到多种约束条件,主要包括机床固有属性约束、零件加工尺寸约束、零件加工质量约束等。
1.3.1 机床约束
(1)主轴转速约束。
切削速度应满足机床主轴转速的约束:

式中:Nmax、Nmin(r/min)分别为机床主轴转速的上下限;D为刀具直径。
(2)进给量约束。
进给量应满足机床进给量的约束:

式中:fmax、fmin( mm/r)分别为机床进给量的上下限。
(3)切削力约束。
机床进给方向切削力应小于主轴最大进给力[5]:
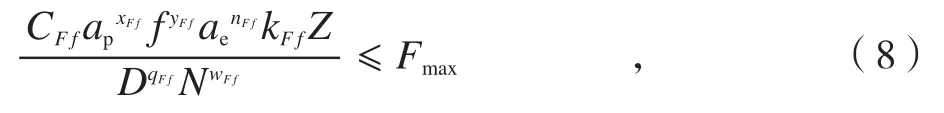
式中:Fmax表示最大进给力;ae为切削宽度,CFf、xFf、yFf、nFf、KFf、qFf、wFf表示与工件材料和切削条件有关的系数,可查阅切削用量手册得到。
(4)切削扭矩约束。
切削扭矩不能超过主轴最大扭矩:

式中:Mfmax为机床主轴的最大扭矩。
(5)切削功率约束。
切削功率应小于机床有效功率:

式中:Fc为切削力,η为机床功率有效系数,Pmax为机床最大功率。
1.3.2 切削深度约束
切削深度的取值范围应限定在给定的最大值和最小值之间:

式中:drL、drU分别为粗加工时所允许的最小最大切削深度,dsL、dsU分别为精加工时所允许的最小最大切削深度。
1.3.3 加工质量约束
零件加工表面的粗糙度应满足零件表面最低粗糙度要求:

式中:rε为刀尖圆弧半径;Rmax为零件表面最低粗糙度要求。
综上所述,本文的铣削参数优化问题是一个典型的约束优化问题,其具体的优化模型如下:

约束条件:

2 基于改进人工蜂群算法的模型求解
2.1 约束的处理
从上文所建立的模型(14)可以看出,切削参数优化模型中存在很多的约束条件,且基本都是非线性不等式约束。而人工蜂群算法是针对无约束优化问题的随机寻优算法[7-9]。因此,在算法中要引入相应的约束处理机制,才可用于解决切削参数优化问题。罚函数法是目前最常用的约束处理方法,其将目标函数与约束条件综合在一个罚函数中。对本文来说,罚函数可表示为:

式中:minF为目标优化函数,a为惩罚因子,m为本文所对应的不等式约束的个数,φi(f)为上文所对应的不等式约束。
在算法迭代时,对于没有违反约束的解= 0,从而而对于违反约束的解会通过罚函数对其进行惩罚,使其解的适应度降低。
2.2 粗车次数n的确定
在实际生产过程中,加工过程每多走刀一次,都会导致时间、成本、能源消耗的增加。因此,在满足切削深度约束的前提下,粗加工次数应尽可能少。而且零件加工表面的粗糙度要求仅由最后一道精加工工序决定,与粗加工次数的多少没有关系。因此,在给定总切削余量d,粗切削深度dr和精切削深度ds的取值范围的条件下,结合上文所述的粗加工次数确定原则,很容易便可确定粗加工次数n的值。n值确定后,本文的切削参数优化问题便可转化成一个3n+3维的函数优化问题。
2.3 改进的人工蜂群算法
2.3.1 基本人工蜂群算法(ABC)
人工蜂群算法是由土耳其学者Karaboga提出的一种模拟蜜蜂群体寻找优良蜜源的智能计算方法。该算法模型主要包括3个基础部分:蜜源,雇佣蜂(也称引领蜂),雇佣蜂(包括侦查蜂和跟随蜂)。3个基本行为模式:搜索蜜源、为蜜源招募、放弃蜜源。每个蜜源的位置代表优化问题的一个可行解,引领蜂的个数与蜜源个数相等,蜜源质量的好坏由解的适应度值决定。初始化以后,引领蜂首先对其对应的蜜源进行邻域搜索,并进行“贪婪”选择,若搜索到的新位置蜜源质量比原来的好,则用新蜜源的位置取代旧蜜源的位置,否则保持不变。所有引领蜂完成邻域搜索以后,会飞回蜂巢在“舞蹈区”跳摇摆舞,通过舞蹈传递所找到的蜜源信息。跟随蜂根据接收到的舞蹈信息,按概率选择所要跟随的引领蜂。引领蜂对应的蜜源质量越好,被选择的概率越大。跟随蜂到达目的地后会重新在蜜源附近搜索新的蜜源,并根据“贪婪”选择原则更新蜜源位置。
引领蜂和跟随蜂在蜜源位置附近进行邻域搜索,根据公式如下:

式中:j代表解的维数,k ∈ {1,2,···,Ne}(Ne代表种群个数),且均随机生成,为区间[-1,1]之间的随机数。
跟随蜂按照概率选择所要跟随的引领蜂,概率的计算公式如下:

式中:fi代表第i个蜜源的适应度值。
此外,为了增强种群多样性,防止种群陷入局部最优,ABC算法预先设置了一个limit参数,如果一个蜜源的位置经过limit次循环后仍不能得到更新,则放弃该蜜源,其所对应的引领蜂变为侦查蜂,重新寻找新的蜜源,新蜜源产生公式如下:

式中:j代表解的维数,rand(0,1)为区间[0,1]之间的随机数。
2.3.2 改进的人工蜂群算法(SP-ABC)
(1)自适应比例选择概率(S-ABC)。
基本ABC算法根据公式(17)计算选择引领蜂的概率。该选择策略过分依赖蜜源的适应度值,在算法前期,质量较好的蜜源被多次选中,而质量较差的蜜源几乎得不到被选择的机会,这限制了种群的多样性。而在算法后期,蜜源的适应度值相差不大,更好的蜜源却得不到更多的选择机会,导致算法后期收敛能力下降。基于此,本文引入了自适应比例选择策略,根据蜜源适应度值的状态自动调整选择压力。具体公式如下:

式中:表示t代中适应度最好的个体,为t代中所有个体适应度的平均值。算法前期,种群适应度值相差较大,较大,λ值较小,选择压力较小,适应度较差的个体也有被选择的机会。算法后期,较小,λ值较大,选择压力较大,适应度较好的个体获得更多被选择的机会,使算法能快速收敛于全局最优解。
(2)混合人工蜂群算法(P-ABC)。
ABC算法最突出的优点是每次迭代中都进行了一次全局搜索和一次局部搜索,因此,算法找到最优解的概率大大提高,且具有很快的收敛速度。但在对局部进行搜索时,只是随机的生成一个新解,并未对局部进行精细搜索。且当某个解搜索次数超过设定的limit值仍未更新位置时,对应的引领蜂转变为侦查蜂后,重新在整个参数范围内随机搜索,没有参照当前解的有用信息,具有很大的随意性。而粒子群算法(PSO)具有较好的全局寻优能力,因此,当某个解搜索次数超过limit值未更新位置时,结合粒子群算法,在当前解附近重新生成一搜索范围,既考虑了当前解的有效信息,又具有相当的全局搜索性能,使侦查蜂能够在一定的范围内做精细搜索,提高了算法性能。
(3)改进的人工蜂群算法(SP-ABC)具体步骤如下:
步骤1 设置参数 蜜源个数=引领蜂个数=跟随蜂个数=SN,设置最大迭代次数MCN,限定进化代数limit。
步骤2 初始化种群,并计算每个初始解的适应度值。
步骤3 引领蜂在当前位置附近进行邻域搜索,按公式(16)产生新的位置vij,根据“贪婪”原则在vij和xij中选择适应度较好一个保留给下一代种群。
步骤4 计算蜜源xi的适应度值,根据公式(19)、(20)计算该蜜源被选择的概率pi。
步骤5 跟随蜂按pi选择所要去的蜜源位置,并在其附近进行邻域搜索(同步骤3)。
步骤6 判断是否有蜜源经过limit次循环后仍未更新其位置,若存在,进入粒子群优化方式。若不存在,转步骤7。
·设置粒子个数N,最大迭代次数Nmax。
·按公式(21)在当前蜜源附近随机生成N个粒子,并随机初始化其速度。

·按照粒子群算法优化得到最优解,即新的蜜源位置。
·用新蜜源的位置代替原蜜源的位置。
步骤7 记录当前最优解及其相应参数。
步骤8 判断是否满足最大迭代数,若满足,则停止迭代,输出最优解;否则,转步骤3。
3 实例仿真
3.1 实例模型参数设置
本文以江苏南通某电梯零部件生产企业加工磁铁安装板为例进行仿真优化,仿真模型参数如下:
加工工件:材质为钢;
加工参数:切削长度159mm,切削深度7mm,切削宽度60mm;
刀具:高速立铣刀,刀具直径10mm,铣刀齿数4,刀具刀尖直径0.8mm;
加工要求:表面粗糙度最大值3.2。
数控铣床规格参数如表1所示。铣削参数优化模型中其他参数为根据上文所述的粗车次数确定原则,可以得出粗车次数n=2,则该实例是一个9维函数优化问题。
3.2 SP-ABC算法中参数设置
SPABC算法中,初始种群数目为100,其中引领蜂和跟随蜂各占一半,最大迭代次数1000次,循环限定次数limit=50。进入粒子群优化模式时,初始化粒子种群数目50,最大迭代数100次,局部加速因子c1= 2.0,全局加速因子c2= 2.0,惯性因子为0.8。

表1 数控铣床规格参数
算法使用MATLAB编程实现,随机运行30次,取平均值,并与其他算法优化结果对比,结果如表2所示。
从表2及表3可以看出,经本文改进人工蜂群算法优化过的结果与传统的GA、PSO及基本ABC算法相比,其优化结果更好、更加稳定,能节省更多的加工成本。由此,可以得出如下结论:改进的人工蜂群算法在求解切削参数优化问题时较基本ABC算法等其他基本算法更加优越。
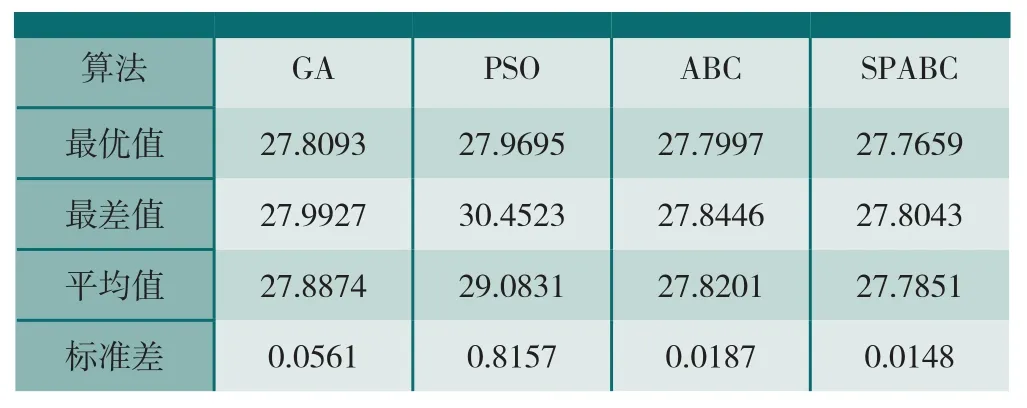
表2 不同算法随机测试30次结果比较

表3 不同算法测试30次最优化结果比较
4 结论
本文以最低加工成本为目标优化函数,综合考虑了实际加工过程中机床固有属性、零件尺寸要求、零件加工表面质量等多方面的条件约束,建立了可同时对多道工序的切削参数同步进行优化的优化函数模型。基于PSO算法和基本ABC算法各自的优点,将两者结合提出了改进的人工蜂群算法,并将此算法得出的优化结果与其他几种基本算法得出的优化结果比较,显示改进的人工蜂群算法能获得比其他基本算法更优的结果,证明了该算法在处理切削参数优化问题上的优越性。
[1] 陈志同,张保国.面向单元切削过程的切削参数优化模型[J].机械工程学报 , 2009,45(5):230-236.CHEN Zhitong,ZHANG Baoguo. Mathematic model on cutting parameter optimization for unit cutting process [J]. Journal of Mechanical Engineering, 2009,45(5):230-236.
[2] 李聪波,崔龙国,刘飞,等.面向高效低碳的数控加工参数多目标优化模型[J].机械工程学报, 2013,49(5):87-96.LI Congbo,CUI Longguo,LIU Fei,et al. Multi-objective NC machining parameters optimization model for high efficiency and low carbon[J]. Journal of Mechanical Engineering, 2013,49(5):87-96.
[3] 张青,陈志同,张平,等. 基于粒子群算法的切削参数优化及其约束处理[J].航空精密制造技术, 2010,46(1):32-36.ZHANG Qing,CHEN Zhitong,ZHANG Ping, et al. An algorithm for cutting parameter optimization and constraint handling based on particle swarm optimization[J]. Javiation Precision Manufacturing Technology,2010,46(1):32-36.
[4] 李新鹏,张超勇,高亮,等. 基于元胞粒子群算法的数控切削参数优化[J].计算机工程与应用, 2014,50(2):252-257.LI Xinpeng,ZHANG Chaoyong,GAO Liang, et al. NC cutting parameter optimization based on cellular particle swarm optimization algorithm [J]. Computer Engineering and Applications, 2014, 50(2):252-257.
[5] 陈志楚,李聪,张超勇. 基于帝国主义竞争算法的切削参数优化 [J].制造业自动化 , 2012,34(12):10-15.CHEN Zhichu,LI Cong,ZHANG Chaoyong. Cutting parameters optimization based on imperialist competitive algorithm[J].ManufacturingAutomation, 2012,34(12):10-15.
[6] 刘畅,王焱. 针对航空难加工材料的刀具与切削参数优化途径 [J].航空制造技术, 2010(8):39-43.LIU Chang,WAN Yan. Cutting tool and cutting parameter optimization path for difficult-to-machine material in aviation industry [J].Aeronautical Manufacturing Technology, 2010(8):39-43.
[7] YILDIZ A R. Optimization of cutting parameters in multi-pass turning using artificial bee colony-based approach[J].Information Sciences,2013, 220:399-407.
[8] 王慧颖,刘建军,王全洲. 改进的人工蜂群算法在函数优化问题中的应用[J].计算机工程与应用, 2013, 48(19):36-39.WANG Huiying, LIU Jianjun, WANG Quanzhou. The application of modified artificial bee colony algorithm in numerical function optimization[J].Computer Engineering and Applications, 2013,48(19):36-39.
[9] 葛宇,梁静,王学平,等.求解函数优化问题的改进的人工蜂群算法 [J].计算机科学 , 2013,40(8):252-257.GE Yu, LIANG Jing, WANG Xueping, et al. Modified artificial bee colony algorithm for numerical function optimization[J]. Computer Science,2013, 40(8):252-257.