(N+1)维广义的Boussinesq方程的精确显式非线性波解

温振庶

(华侨大学 数学科学学院， 福建 泉州 362021)



(N+1)维广义的Boussinesq方程的精确显式非线性波解

温振庶

(华侨大学 数学科学学院， 福建 泉州 362021)

摘要：研究(N+1)维广义的Boussinesq方程的非线性波解.利用动力系统定性理论和分支方法,获得它的多种非线性波解的精确显式表达式，这些解包括孤立波解，爆破解，周期爆破解和扭波型解.

关键词：(N+1)维广义的Boussinesq方程； 孤立波解； 爆破解； 周期爆破解； 扭波型解

2007年，Yan[1]引入(N+1)维广义的Boussinesq方程,即

(1)

式(1)中：τ≠0是常数；N>1是一个整数.文献[1]利用半行波相似变换得到几类解.Guo等[2]采用辅助方程方法得到方程(1)的几种Jacobi椭圆函数解.Liu等[3]研究(2+1)维Boussinesq方程的精确周期孤立波解，即

(2)

Abdel等[4]研究(2+1)维广义的Boussinesq方程的孤立波解，即

(3)

本文从动力系统的角度[4-21]研究方程(1)的非线性波解，获得它的多种非线性波解的精确显式表达式，这些解包括孤立波解，爆破解，周期爆破解和扭波型解.

1分支相图

(4)

对式(4)积分两次，并设积分常数为0，得到

(5)

令y=φ′，得到一个平面系统,即

(6)

其首次积分为

(7)

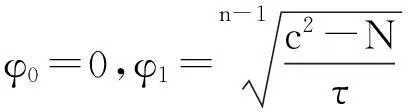
假设(φi,0)是系统(6)的一个奇点，系统(6)的线性化系统在奇点(φi,0)的特征值为

根据动力系统的定性理论，有如下引理1.

引理1当n是偶数时，有

1) 如果c2-N>0，且τ>0，则φ1>0=φ0，且(φ0,0)是一个鞍点，而(φ1,0)是一个中心.

2) 如果c2-N>0，且τ<0，则φ1<0=φ0，且(φ0,0)是一个鞍点，而(φ1,0)是一个中心.

3) 如果c2-N<0，且τ>0，则φ1<0=φ0，且(φ0,0)是一个中心，而(φ1,0)是一个鞍点.

4) 如果c2-N<0，且τ<0，则φ1>0=φ0，且(φ0,0)是一个中心，而(φ1,0)是一个鞍点.

当n是奇数时，有

1) 如果c2-N>0，且τ>0，则-φ1<0=φ0<φ1，且(φ0,0)是一个鞍点，而(±φ1,0)是中心.

2) 如果c2-N<0，且τ<0，则-φ1<0=φ0<φ1，且(φ0,0)是一个中心，而(±φ1,0)是鞍点.

证明通过分析系统(6)的线性化系统在奇点的特征值，很容易证明引理1.

因此，基于以上分析，得到系统(6)的分支相图如图1，2所示.

(a) c2-N>0，τ>0　　　　　　　　　　　　　　　　(b) c2-N>0，τ<0

(c) c2-N<0，τ>0　　　　　　　　　　　　　　　　(d) c2-N<0，τ<0图1　当n为偶数时系统(6)的分支相图Fig.1　Phase portraits of system (6) when n is even

(a) c2-N>0，τ>0　　　　　　　　　　　　　　　　(b) c2-N<0，τ<0图2　当n为奇数时系统(6)的分支相图Fig.2　Phase portraits of system (6) when n is odd

2主要结果及其理论证明

命题11) 当n为偶数，且c2-N>0时，方程(1)有孤立波解、爆破解，表达式分别为

(8)

(9)

2) 当n为偶数，且c2-N<0时，方程(1)有周期爆破解，表达式为

(10)

证明1) 当c2-N>0时，在图1(a)和图1(b)中有一条通过鞍点(φ0,0)的同宿轨.根据式(7)可以得到同宿轨的表达式为

(11)

(12)

把式(11)或式(12)代入系统(6)的第一个方程，并沿着同宿轨积分，得到

(13)

(14)

(15)

(16)

根据式(13)或式(14)，得到式(8)中的孤立波解u1；而根据式(15)或式(16)，可以得到式(9)中的爆破解u2.

2) 当c2-N<0时，在图1(c)和图1(d)中有一条与中心(φ0,0)的Hamiltonian相同的轨道.根据式(7)，此轨道的表达式为式(11)或式(12).把式(11)或式(12)代入到系统(6)的第一个方程，并沿着此轨道积分，得到式(15)或式(16).由此，得到式(10)中的周期爆破解u3.

命题21) 当n为偶数，且c2-N<0时，方程(1)有孤立波解和爆破解.特别地，取n=2，孤立波解和爆破解的表达式分别为

(17)

(18)

2) 当n为偶数，且c2-N>0时，方程(1)有周期爆破解.特别地，取n=2，周期爆破解的表达式为

(19)

证明1) 当c2-N<0时，在图1(c)和图1(d)中有一条通过鞍点(φ1,0)的同宿轨.由分支方法知，方程(1)有孤立波解和爆破解.特别地，取n=2，则由式(7)，得到同宿轨的表达式为

(20)

(21)

把式(20)或式(21)代入到系统(6)的第一个方程，并沿着同宿轨积分，得到

(22)

(23)

(24)

(25)

由式(22)或式(23)，得到式(17)的孤立波解u4，而根据式(24)或式(25)，得到式(18)的爆破解u5.

2) 当c2-N>0时，在图1(a)和图1(b)中有一条与中心(φ1,0)的Hamiltonian相同的轨道.

由分支方法知，方程(1)有孤立波解和爆破解.特别地，取n=2，则由式(7)，把式(20)或式(21)代入系统(6)的第一个方程，并沿着此轨道积分，可以得到式(24)或式(25).由此，也就得到式(19)中的周期爆破解u6.

命题31) 当n为奇数，且c2-N>0,τ>0时，方程(1)有孤立波解，表达式为

(26)

2) 当n为奇数，且c2-N<0,τ<0时，方程(1)有周期爆破解，即

(27)

此外，方程(1)有扭波型解和爆破解.特别地，取n=3，扭波型解和爆破解的表达式分别为

(28)

(29)

式(28)中：β≥0是一个实数.

特别地，取n=5，扭波型解为

(30)

式(30)中：γ是一个任意的实数.

此外，图2(b)中还有两条连接两个鞍点(φ1,0)和(-φ1,0)的异宿轨，由分支方法知，方程(1)有扭波型解和爆破解.特别地，取n=3，则由式(7)，异宿轨的表达式为

(31)

把式(31)代入到系统(6)的第一个方程，并沿着异宿轨积分，得到

(32)

(33)

类似地，取n=5，异宿轨的表达式为

(34)

把式(34)代入系统(6)的第一个方程，并沿着异宿轨积分，得到

(35)

3结束语

利用动力系统定性理论和分支方法，研究(N+1)维广义的Boussinesq方程的非线性波解，获得它的多种非线性波解的精确显式表达式，这些解包括孤立波解，爆破解，周期爆破解和扭波型解.

参考文献：

[1]YANZhenya.Similaritytransformationsandexactsolutionsforafamilyofhigher-dimensionalgeneralizedBoussinesqequations[J].PhysicsLettersA,2007,361(3):223-230.

[2]GUOYunxi,LAIShaoyong.Newexactsolutionsforan(n+1)-dimensionalgeneralizedBoussinesqequation[J].NonlinearAnalysis:Theory,MethodsandApplications,2010,72(6):2863-2873.

[3]LIUChangfu,DAIZhengde.Exactperiodicsolitarywavesolutionsforthe(2+1)-dimensionalBoussinesqequation[J].JournalofMathematicalAnalysisandApplications,2010,367(2):444-450.

[4]ABDELRADYA,OSMANE,KHALFALLAHM.Onsolitonsolutionsofthe(2+1)-dimensionalBoussinesqequation[J].AppliedMathematicsandComputation,2012,219(8):3414-3419.

[5]SONGMing,SHAOShuguang.Exactsolitarywavesolutionsofthegeneralized(2+1)-dimensionalBoussinesqequation[J].AppliedMathematicsandComputation,2010,217(7):3557-3563.

[6]刘正荣，唐昊.KdV方程和mKdV方程的新奇异解[J].华南理工大学学报(自然科学版),2012，40(10):96-101.

[7]WENZhenshu.Bifurcationofsolitons,peakons,andperiodiccuspwavesforθ-equation[J].NonlinearDynamics,2014,77(1/2):247-253.

[8]WENZhenshu.Severalnewtypesofboundedwavesolutionsforthegeneralizedtwo-componentCamassa-Holmequation[J].NonlinearDynamics,2014,77(3):849-857.

[9]WENZhenshu.Bifurcationsandnonlinearwavesolutionsforthegeneralizedtwo-componentintegrableDullin-Gottwald-Holmsystem[J].NonlinearDynamics,2015,82(1/2):767-781.

[10]WEN Zhenshu.Extension on peakons and periodic cusp waves for the generalization of the Camassa-Holm equation[J].Mathematical Methods in the Applied Sciences,2015,38(11):2363-2375.

[11]WEN Zhenshu,LIU Zhengrong.Bifurcation of peakons and periodic cusp waves for the generalization of the camassa-holm equation[J].Nonlinear Analysis: Real World Applications,2011,12(3):1698-1707.

[12]WEN Zhenshu,LIU Zhengrong,SONG Ming.New exact solutions for the classical drinfel′d-sokolov-wilson equation[J].Applied Mathematics and Computation,2009,215(6):2349-2358.

[13]WEN Zhenshu.Bifurcation of traveling wave solutions for a two-component generalized θ-equation[J].Mathematical Problems in Engineering,2012,2012:1-17.

[14]WEN Zhenshu.Extension on bifurcations of traveling wave solutions for a two-component fornberg-whitham equation[J].Abstract and Applied Analysis,2012,2012:1-15.

[15]WEN Zhenshu.New exact explicit nonlinear wave solutions for the Broer-Kaup equation[J].Journal of Applied Mathematics,2014,2014:1-7.

[16]温振庶.耦合的修正变系数KdV方程的非线性解[J].华侨大学学报(自然科学版),2014，35(3):597-600.

[17]温振庶.几类非线性数学物理方程及系统生物学模型的研究[D].广州：华南理工大学,2012：1-143.

[18]刘正荣.分支方法与广义 CH 方程的显式周期波解[J]. 华南理工大学学报(自然科学版),2007,35(10):227-232.

[19]唐民英,王瑞琦.具有高阶非线性项的广义 KdV 方程的孤立波及其分支[J].中国科学:A 辑,2002,32(5):398-409.

[20]曹军,鲁慧媛.广义 Davey-Stewartson 的精确解[J].上海师范大学学报(自然科学版),2015,44(3):330-338.

[21]SONG M,LIU Z. Qualitative analysis and explicit traveling wave solutions for the Davey-Stewartson equation[J].Mathematical Methods in the Applied Sciences,2014,37(3):393-401.

(责任编辑： 陈志贤英文审校：黄心中 )

Exact Explicit Nonlinear Wave Solutions for the (N+1)-Dimensional Generalized Boussinesq Equation

WEN Zhenshu

(School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China)

Abstract：In this paper, we study the nonlinear wave solutions for the (N+1)-dimensional generalized Boussinesq equation. Using the bifurcation method and qualitative theory of dynamical systems, we obtain many exact explicit expressions of the nonlinear wave solutions for the equation. These solutions contain solitary wave solutions, blow-up solutions, periodic blow-up solutions, and kink-shaped solutions.

Keywords：(N+1)-dimensional generalized boussinesq equation; solitary wave solutions; blow-up solutions; periodic blow-up solutions; kink-shaped solutions

中图分类号：O 175.29

文献标志码：A

基金项目：国家自然科学基金资助项目(61573004， 11401230)； 福建省自然科学基金资助项目(2015J05008)； 福建省教育厅科技项目(JA14023)

通信作者：温振庶(1984-)，男，副教授，博士，主要从事微分方程与动力系统的研究.E-mail:wenzhenshu@hqu.edu.cn.

收稿日期：2015-11-19

doi:10.11830/ISSN.1000-5013.2016.03.0380

文章编号：1000-5013(2016)03-0380-06