电场类三线问题的命题特点和教学策略

潘华君

(江苏省宜兴第一中学,江苏　宜兴　214206)



·试题研究·

电场类三线问题的命题特点和教学策略

潘华君

(江苏省宜兴第一中学,江苏宜兴214206)

摘要：电场类三线问题串接了力的分析、运动的分析、功能关系的分析及相关电场知识,能考查学生知识掌握程度、运用相关方法分析的熟练程度、以及综合分析的能力等,故历来深受命题专家的青睐．本文以2015年全国各地高考卷为蓝本,分析该类试题的命题特点和布局,并给出相关的教学建议．

关键词：电场;三线问题;特点;教学策略

所谓“三线”问题,是指以静电场中的电场线、等势面(为便于归类,下文称为等势线)为背景,依托带点粒子的运动轨迹线,对粒子的电性和电量、结合运动状态分析受力、结合受力分析运动、功能关系等相关问题进行考查,该类试题是历年各地高考卷中常考题型,更是其它拓展问题的基准点．本文对2015年全国各地的高考卷做一梳理,明确该类问题的命题规律,同时提出相关的处理策略,从而进一步提高高三复习教学的针对性和有效性．

1比较分析

1.1模型比重

对2015年各地高考卷中的“三线问题”归类统计发现,其中涉及“等势面(线)”出现2例,涉及“电场线问题”的为2例,涉及“轨迹线问题”的有9例．利用Excel相关功能统计比较得到图1，由此可见,有关“轨迹线”的问题占有的比重最大,值得引起重视．

图1

1.2题型比重

以上述统计的13道“三线问题”为例,研究它们在整个试卷中的各个题型分布,具体情况如图2所示，由此可知,该类试题主要分布在选择题部分．

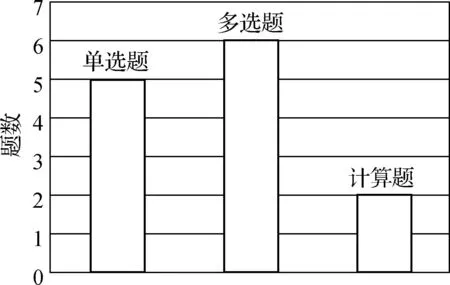
图2

2典型问题及应对策略

2.1等势线问题

图3

例1(2015年海南卷):如图3所示,两电荷量分别为Q(Q>0)和-Q的点电荷对称地放置在x轴上原点O的两侧,a点位于x轴上O点与点电荷Q之间,b位于y轴O点上方．取无穷远处的电势为零,下列说法正确的是().

A.b点的电势为零,电场强度也为零

B. 正的试探电荷在a点的电势能大于零,所受电场力方向向右

C. 将正的试探电荷从O点移到a点,必须克服电场力做功

D. 将同一正的试探电荷先后从O、b点移到a点,后者电势能的变化较大

解析:等量异种电荷连线的中垂线为等势线,由于取无穷远处为零电势,则中垂线上各点的电势均为零,故b点的电势为零,但是电场强度不为零;由于φa>φO=0,故正电荷在a处电势能为正;由W=UO aq，且φa>φO知,将正的试探电荷从O点移到a点,电场力做负功;O点和b点的电势相等,所以先后从O、b点移到a点,电场力做功相等,电势能变化相同．故选项B、C正确.

2.2电场线问题

图4

例2(2015年江苏卷):两个相同的负电荷和一个正电荷附近的电场线分布如图4所示,c是两负电荷连线的中点,d点在正电荷的正上方,c、d到正电荷的距离相等,则().

A．a点的电场强度比b点的大

B．a点的电势比b点的高

C．c点的电场强度比d点的大

D．c点的电势比d点的低

解析:由“电场线的疏密表示该处电场强度的大小”可知选项A、C正确.过a的等势面与b点所在电场线的交点在b点沿电场线的方向上,故a点的电势比b点的低.由于c、d到正电荷的距离相等,且在正电荷到c与正电荷到d的对应位置处,前者电场线密,场强大,则由U=Ed定性分析可知,正电荷到c的这段距离上电势降落较多,则c点的电势比d点的低，选项B错误、D正确．

命题特点及应对策略:从历年各地高考卷中有关等势线问题、电场线问题分析来看,主要存在以下几个特点:① 试题常以单点电荷、等量同种或异种电荷等模型的电场线、等势面的分布为背景材料来进行命题或适度拓展;② 在考查的问题中,往往会将有关的电场线问题和电势问题结合在一起考查,由电场线分析等势线,或是由等势线分析电场线,即单一的考查较为少见．

鉴于以上命题特点,笔者认为在实际的教学中,应引导学生牢固掌握以下四点:

(1) 要引导学生熟悉教材上常见模型的电场线和等势面的分布特点,这些模型均是各类考题命制的出发点,把握住这些基本问题,有助学生突破试题的迷惑情景，抓住题眼,快速构建恰当模型，明确入手点．

(2) 引导学生明确两线疏密程度代表的物理意义和“线线垂直”的特点．

(3) 关于电势高低判断有三法,一是在同一条电场线上,沿线方向电势降低;二是在不同电场线上,可以依据线面垂直的关系,先通过某点作等势面,后依据“方法一”判断;三是从电场力做功的表达式W=U12q中推导出两点的电势高低．

(4) 在实际教学中,可以从两个角度入手,一是从“点”入手,如在分析等量异种电荷连线和中垂线上,可以取一些特征点,运用场强叠加原理,分析合场强的变化趋势;二是引导学生从“面”上入手,即依据电场线分布特点分析场强的变化趋势和电势的变化趋势．由此“点”“面”结合,使得学生对基本模型的分布情形能够了然于胸．

2.3轨迹线问题

图5

例3(改编自2015年安徽卷):如图5所示,在xOy平面内,有沿y轴负方向的匀强电场,场强大小为E(图中未画出),由A点斜射出一质量为m,带电荷量为q的粒子,B和C是粒子运动轨迹上的两点,其中l0为常数．粒子所受重力忽略不计．

(1) 判断粒子的电性.

(2) 求粒子从A到C过程中电场力对它做的功.

(3) 求粒子从A到C过程所经历的时间.

(4) 求粒子经过C点时的速率．

解析:(1) 过A点作切线得A处粒子的速度方向,同时由粒子轨迹的偏向可得该粒子必受竖直向下的电场力,则该粒子必带正电.

(2) 粒子从A到C过程中电场力对它做的功为W=3Eql0.

例4(2015年江苏卷):如图6所示,一带正电的小球向右水平抛入范围足够大的匀强电场,电场方向水平向左,不计空气阻力,则小球().

A． 做直线运动

B． 做曲线运动

C． 速率先减小后增大

D． 速率先增大后减小

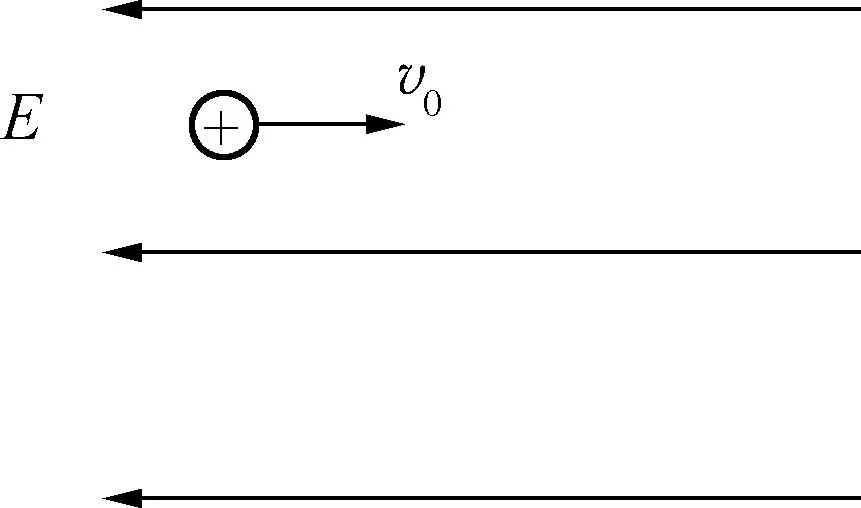
图6

解析:由题意知,小球受重力、电场力作用,合力方向与初速度方向不共线,且夹角为钝角,故小球做曲线运动.在运动的过程中合外力先做负功后做正功，故小球速率先减小后增大．选项B、C正确.

命题特点及应对策略:例3和例4分别代表了轨迹线类问题的两种命题趋势——已知轨迹分析相关量、已知受力和初始速度分析运动轨迹．这两类问题是牛顿运动定律中两个基本问题——已知运动求力和结合受力分析运动的具体化,是动力学的最基本、也是最重要的问题．对于第一类题型,要引导学生注意分清轨迹中的“三向”,即速度方向、合力方向、轨迹的偏向,由曲线运动相关知识可知,轨迹与速度相切,夹于合力方向和速度方向之间,且偏向合力的方向．因此,只要“三向”中有“两向”已知,就可以判断“第三向”．在具体的问题求解中,应建议学生在已知轨迹上选取一个特征点,作出切线方向,得到该点处的速度方向,然后依据轨迹偏向得到合力方向,最后依据合力、速度方向等判断粒子电性、做功、能量转化等问题．对于第二类题型,要引导学生明确力与运动的关系,综合运用运动学知识、动力学知识、功能关系等分析．在具体教学中,可以选择一些典型性的例题加以强化,同时不断渗透、提升动力学中两类基本问题的分析能力．另一方面,这也提示我们在平时的教学中,对于牛顿运动定律的两类基本问题要有足够的重视,不能因其看似简单而一带而过．

参考文献：

[1]潘华君.品说明变化思应对策略[J].物理之友,2015，31(4)．

[2]任才生,潘华君.年年岁岁花相似岁岁年年题不同[J].物理教师,2014，(6)．