聚焦圆锥曲线的热点问题

佘媛媛++张世林

1.怎么考

本部分主要以解答题形式考查，往往是试卷的压轴题之一，一般以直线与圆锥曲线、圆与圆锥曲线为载体，考查弦长、定点、定值、最值、范围问题或探索性问题，试题难度较大，能力要求高，综合性强.

2.怎么办

（1）圆锥曲线的最值与范围问题的常见解法：①几何法：若题目的条件和结论能明显体现几何特征和意义，则考虑利用图形性质来解决；②代数法：若题目的条件和结论能体现一种明确的函数关系，则可首先建立目标函数，再求这个函数的最值.

（2）定值、定点问题必然是在变化中所表现出来的不变的量，处理时直接推理求出定值，也可先通过特定位置猜测结论后进行一般性证明，对于客观题，通过特殊值法探求定点、定值能达到事半功倍的效果.

（3）探索性问题主要是存在性问题，求解时一般先假设存在，然后进行合理的推理论证，若得到的结论符合情理则假设成立，若得到矛盾的结论则假设不成立.

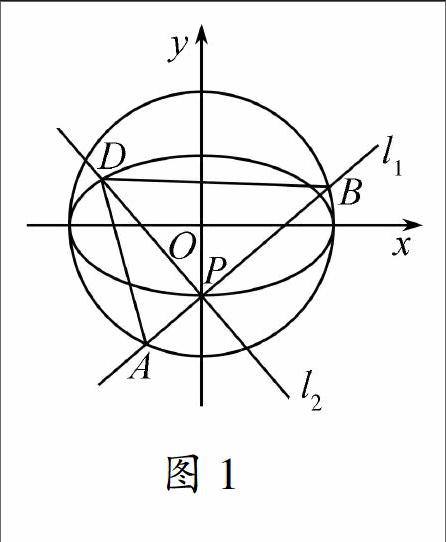
热点一圆锥曲线中的范围、最值问题图1

例1如图1，点P（0，-1）是椭圆C1：x2a2+y2b2=1（a>b>0）的一个顶点，C1的长轴是圆C2：x2+y2=4的直径.l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A，B两点，l2交椭圆C1于另一点D.

（1）求椭圆C1的方程；

（2）求△ABD面积取最大值时直线l1的方程.

解（1）由题意得a=2，b=1，所以椭圆C1的方程为x24+y2=1.

（2）设A（x1，y1），B（x2，y2），D（x0，y0），由题意知直线l1的斜率存在，不妨设其为k，则直线l1的方程为y=kx-1.又圆C2：x2+y2=4，故点O到直线l1的距离d=1k2+1，所以AB=24-d2=24k2+3k2+1，又l1⊥l2，故直线l2的方程为x+ky+k=0.

由x+kx+k=0，

x2+4y2=4消去y，整理得（4+k2）x2+8kx=0，故x0=-8k4+k2，所以PD=8k2+14+k2.设△ABD的面积为S，则S=12AB·PD=84k2+34+k2，

所以S=324k2+3+134k2+3≤161313，当且仅当k=±102时取等号.故所求直线l1的方程为y=±102x-1.

思维升华求最值及参数范围的方法有两种：①根据题目给出的已知条件或图形特征列出一个关于参数的函数关系式，将其代入由题目列出的不等式（即为消元），然后求解不等式；②由题目条件和结论建立目标函数，进而转化为求函数的值域.在利用代数法解决最值与范围问题时常从以下五个方面考虑：

①利用判别式来构造不等关系，从而确定参数的取值范围；

②利用已知参数的范围，求新参数的范围，解这类问题的核心是在两个参数之间建立等量关系；

③利用隐含或已知的不等关系建立不等式，从而求出参数的取值范围；

④利用基本不等式求出参数的取值范围；

⑤利用函数值域的求法，确定参数的取值范围.

热点二圆锥曲线中的定值、定点问题

例2已知椭圆C的中点在原点，焦点在x轴上，离心率等于12，它的一个顶点恰好是抛物线x2=83y的焦点.

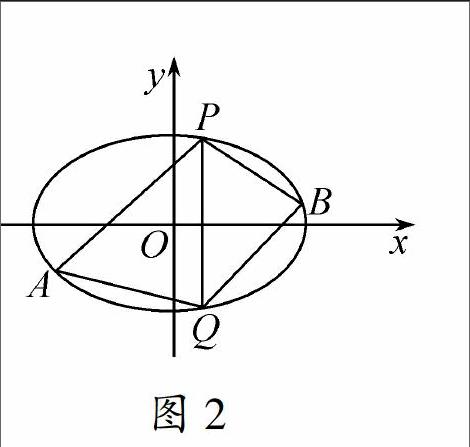
（1）求椭圆C的方程；图2

（2）已知点P（2，3），Q（2，-3）在椭圆上，如图2，点A、B是椭圆上不同的两个动点，且满足∠APQ=∠BPQ，试问直线AB的斜率是否为定值，请说明理由.

解（1）设椭圆C的方程为x2a2+y2b2=1（a>b>0），则b=23.由ca=12，a2=c2+b2，得a=4，所以椭圆C的方程为x216+y212=1.

（2）当∠APQ=∠BPQ时，PA，PB的斜率之和为0，设直线PA的斜率为k，则PB的斜率为-k，PA：y-3=k（x-2），由y-3=k（x-2），

x216+y212=1整理得

（3+4k2）x2+8（3-2k）kx+4（3-2k）2-48=0，x1+2=8（2k-3）k3+4k2，同理PB的直线方程为y-3=-k（x-2），可得x2+2=8k（2k+3）3+4k2.

所以x1+x2=16k2-123+4k2，x1-x2=-48k3+4k2，kAB=y1-y2x1-x2=k（x1+x2）-4kx1-x2=12，所以直线AB的斜率为定值12.

思维升华定值问题就是在运动变化中寻找不变量的问题，基本思想是使用参数表示要解决的问题，证明要解决的问题与参数无关.在这类试题中选择消元的方向是非常关键的.

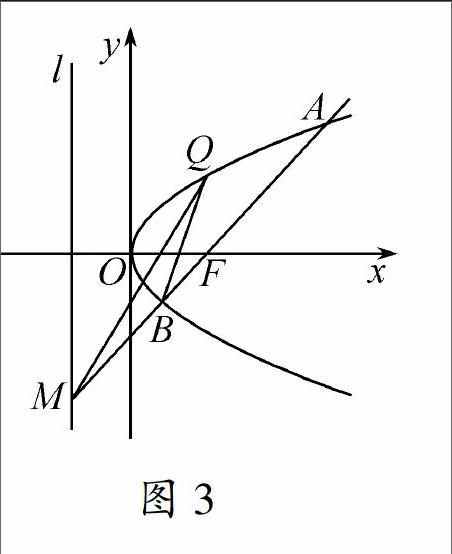
热点三圆锥曲线中的探索性问题图3

例3如图3，抛物线C：y2=2px的焦点为F，抛物线上一定点Q（1，2）.

（1）求抛物线C的方程及准线l的方程.

（2）过焦点F的直线（不经过Q点）与抛物线交于A，B两点，与准线l交于点M，记QA，QB，QM的斜率分别为k1，k2，k3，问是否存在常数λ，使得k1+k2=λk3成立，若存在λ，求出λ的值；若不存在，说明理由.

解（1）把Q（1，2）代入y2=2px，得2p=4，所以抛物线方程为y2=4x，准线l的方程：x=-1.（2）由条件可设直线AB的方程为y=k（x-1），k≠0.由抛物线准线l：x=-1，可知M（-1，-2k）.又Q（1，2），所以k3=2+2k1+1=k+1，把直线AB的方程y=k（x-1），代入抛物线方程y2=4x，并整理，可得k2x2-2（k2+2）x+k2=0，设A（x1，y1），B（x2，y2），由根与系数的关系知x1+x2=2k2+4k2，x1x2=1，又Q（1，2），则k1=2-y11-x1，k2=2-y21-x2，因为A，F，B共线，所以kAF=kBF=k，即y1x1-1=y2x2-1=k，所以k1+k2=2-y11-x1+2-y21-x2=2kx1x2-（2k+2）（x1+x2）+2k+4x1x2-（x1+x2）+1=2（k+1），即存在常数λ=2，使得k1+k2=2k3成立.

思维升华解析几何中的探索性问题，从类型上看，主要是存在类型的相关题型.解决问题的一般策略是先假设结论成立，然后进行演绎推理或导出矛盾，即可否定假设或推出合理结论，验证后肯定结论，对于“存在”或“不存在”的问题，直接用条件证明或采用反证法证明.解答时，不但需要熟练掌握圆锥曲线的概念、性质、方程及不等式、判别式等知识，还要具备较强的审题能力、逻辑思维能力以及运用数形结合的思想分析问题和解决问题的能力.

模拟精练

1.已知椭圆C：x2a2+y2b2=1（a>b>0）的离心率为22，其左、右焦点分别是F1、F2，过点F1的直线l交椭圆C于E、G两点，且△EGF2的周长为42.

（1）求椭圆C的方程；

（2）若过点M（2，0）的直线与椭圆C相交于两点A、B，设P为椭圆上一点，且满足OA+OB=tOP（O为坐标原点），当PA-PB<253时，求实数t的取值范围.

答案（1）x22+y2=1；（2）（-2，-263）∪（263，2）.图4

2.如图4所示，椭圆C1：x2a2+y2b2=1（a>b>0）的离心率为22，x轴被曲线C2：y=x2-b截得的线段长等于C1的短轴长.C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A，B，直线MA，MB分别与C1相交于点D，E.

（1）求C1，C2的方程；

（2）求证：MA⊥MB；

（3）记△MAB，△MDE的面积分别为S1，S2，若S1S2=λ，求λ的取值范围.

答案（1）x22+y2=1；（2）略；（3）[916，+∞）.

3.已知双曲线C：x2a2-y2b2=1（a>0，b>0）的焦距为27，其一条渐近线的倾斜角为θ，且tanθ=32.以双曲线C的实轴为长轴，虚轴为短轴的椭圆记为E.

（1）求椭圆E的方程；

（2）设点A是椭圆E的左顶点，P、Q为椭圆E上异于点A的两动点，若直线AP、AQ的斜率之积为-14，问直线PQ是否恒过定点？若恒过定点，求出该点坐标；若不恒过定点，说明理由.

答案（1）x24+y23=1；（2）直线PQ恒过定点（1，0）.

4.已知椭圆C的左，右焦点分别为F1，F2，椭圆的离心率为12，且椭圆经过点P（1，32）.

（1）求椭圆C的标准方程；

（2）线段PQ是椭圆过点F2的弦，且PF2=λF2Q，求△PF1Q内切圆面积最大时实数λ的值.

答案（1）x24+y23=1；（2）λ=1.