圆锥曲线“中点弦”的一个判定定理及其应用
2016-05-24 07:55云南省滇西科技师范学院数理系677000潘继军
中学数学研究(江西) 2016年5期
云南省滇西科技师范学院数理系 (677000) 潘继军
圆锥曲线“中点弦”的一个判定定理及其应用
云南省滇西科技师范学院数理系(677000)潘继军
定理如果MN是圆锥曲线D:f(x,y)=Ax2+By2+C=0上以点P(x0,y0)为中点的弦,弦MN的垂直平分线l的倾斜角为α,O为坐标原点,则存在点M、N关于直线l对称的充要条件是


(Asin2α+Bcos2α)t2-(2Ax0sinα-2By0cosα)t+f(x0,y0)=0①.

由于MN被直线l平分,由t的几何意义知

反之,若(1)、(2)同时成立,则有





证明:设直线l的倾斜角为α,由以上定理知存在点M、N关于直线l对称的充要条件是
由题意知sinα·cosα≠0,所以

所以直线l与D的对称轴不平行时,存在点M、N关于直线l对称的充要条件是


由已知条件A>0,B>0得Ak2+B>0,所以

下面举例说明以上结论在高考题中的具体应用.

图1
(Ⅰ)求实数m的取值范围;
(Ⅱ)求ΔAOB面积的最大值(O为坐标原点).






(Ⅰ) 过点A(2,1)的直线l与所给的双曲线交于两点P1及P2,求线段P1P2的中点P的轨迹方程.
(Ⅱ)过点B(1,1)能否作直线m,使m与所给双曲线交于两点Q1及Q2,且B点是线段Q1Q2的中点?这样的直线m如果存在,求出它的方程;如果不存在,说明理由.


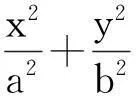
(Ⅰ)求椭圆的标准方程;

图2
(Ⅱ)过F的直线与椭圆交于A、B两点,线段AB的垂直平分线分别交直线l和AB于点P、C,若PC=2AB,求直线AB的方程.

由于PC⊥AB,所以直线PC的方程为y-n=



±1.
所以直线AB的方程为y=x-1或y=-x+1.

析证:显然MN⊥x轴不可能;若MN∥x轴,则弦MN的垂直平分线l为y轴,这时x0=0,显然有



猜你喜欢
河北理科教学研究(2020年2期)2020-09-11
河北理科教学研究(2020年4期)2020-03-09
北京航空航天大学学报(2017年1期)2017-11-24
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16
中学数学杂志(2015年9期)2015-01-01
电子设计工程(2014年18期)2014-02-27
今日中学生(初三版)(2013年6期)2013-07-30
中学理科·综合版(2008年9期)2008-10-15
中学生数理化·高二版(2008年11期)2008-06-17

