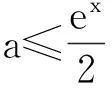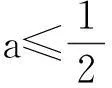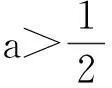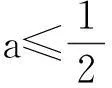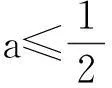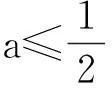“转换”策略在课标卷把关题中的应用探析*

福建省漳州市第一中学　(363000)　刘开富　林新建



“转换”策略在课标卷把关题中的应用探析*

福建省漳州市第一中学(363000)刘开富林新建

解题需要套路，看到一道题，你的第一反应是什么？迅速生成常规方案，也即第一方案.

为什么要有套路？因为80%的高考题是基本的、稳定的，考查运算的敏捷性.没有套路，就没有速度.比如，如何求函数的单调区间、证明函数的单调性；涉及参数问题时，把参数分离出来，转化为这个参数与一个式子的不等或者相等关系；数列问题，设法转化为基本数列(等差数列或等比数列)模型；解析几何问题，根据条件特征选择适当的算法：坐标、向量和运用几何性质推演；概率计算，把一事件转化为互斥事件的和或独立事件的积，合理选用基本模型和分布；…等等.

问题是，当实施第一方案(套路)遇到障碍时，我们的策略是什么？

转换视角，生成第二方案.转换视角，转换到哪里？转换到知识丰富领域，也就是说把问题转换到我们最熟悉的领域.

处理数学难题，从方法论的角度讲就是转换视角.常态方案不行，换一个方案行了；这种说法与思路不通，换一个说法通了；在一个领域内繁复的问题，换一个领域简单了.

如若不是这样，靠什么考查能力？又凭什么说高考是一种选拔性考试呢？

所谓试题的创新，本质上是视角的转换，我们的解题就是要用创新应对创新，用转换适应转换.

1．条件转换

对问题的某个条件作转换，如式的恒等变形，语意的等价转换等，这种转换的目的是使问题简单化、熟悉化.

例1(2010年高考新课标卷Ⅰ文科21题)

设函数f(x)=x(ex-1)-ax2.

(Ⅱ)若当x≥0时f(x)≥0，求a的取值范围.

解析：第(Ⅰ)问不难.

第(Ⅱ)问，f(x)=x(ex-1-ax)，令g(x)=ex-1-ax，则g′(x)=ex-a.

若a≤1，则当x∈(0,+∞)时，g′(x)>0，g(x)为增函数，而g(0)=0，从而当x≥0时g(x)≥0，即f(x)≥0.

若a>1，则当x∈(0,lna)时，g′(x)<0，g(x)为减函数，而g(0)=0，从而当x∈(0,lna)时g(x)<0，即f(x)<0.

综合得a的取值范围为(-∞,1].

评析：本题第(Ⅱ)问直接求解很难，我们通过将f(x)=x(ex-1)-ax2化为f(x)=x(ex-1-ax)，因为x≥0，所以条件“当x≥0时f(x)≥0”可转换为“当x≥0时，g(x)=ex-1-ax≥0”.这样一转换，问题变得简单易解，凸显了“转换策略”在求解数学难题中的重要作用.

例2(2007年高考全国卷Ⅱ理科22题)

已知函数f(x)=x3-x.

(Ⅰ)求曲线y=f(x)在点M(t,f(t))处的切线方程；

(Ⅱ)设a>0，如果过点(a,b)可作曲线y=f(x)的三条切线，证明：-a

解析：第(Ⅰ)问容易，求导得切线的斜率为k=3t2-1，进而由点斜式即得切线方程为y=(3t2-1)x-2t3.

难在第(Ⅱ)问，“过点(a,b)可作曲线y=f(x)的三条切线”，什么意思？如何下手？

如果我们把第(Ⅱ)问的条件换个说法，变为曲线y=f(x)的三条切线都过点(a,b)，也就是说存在三个t，使得直线y=(3t2-1)x-2t3过点(a,b)，或者说，关于t的三次方程b=(3t2-1)a-2t3有三个相异的实数根.

这么一转换，问题可轻松获解.令g(t)=2t3-3at2+a+b，则问题进一步转换为曲线y=g(t)的图像与t轴有三个交点.注意到三次函数只有两种形态：一是没有极值点，一是有两个极值点.于是，这个三次函数的图像应该是：先单调上升经过t轴达到极大值，再单调下降经过t轴达到极小值，而后单调上升第三次经过t轴.

这样问题就归结为[g(t)]极大>0，[g(t)]极小<0，进而由极大值g(0)=a+b>0，极小值g(a)=-a3+a+b=b-f(a)<0，问题得证.

评析：本题第(Ⅱ)问获解的关键也是条件转换，将“过点(a,b)可作曲线y=f(x)的三条切线”转换为“曲线y=f(x)的三条切线都过点(a,b)”，使得问题变得清晰熟悉，易于求解.

2．结论转换

对问题的结论作转换，如恒等变形、等价转化等，这种转换的目的是使问题简单化、明朗化.

例3(2014年高考新课标卷Ⅰ理科21题)

(Ⅰ)求a，b；(Ⅱ)证明： f(x)>1.

3．命题转换

根据命题的等价性进行转换等，这种“不同说法”之间的转换常常可以使那些“理不清”或“说不清”的问题变得容易判断、理解.

例4(2010年高考新课标卷Ⅰ理科21题)

设函数f(x)=ex-1-x-ax2.

(Ⅰ)若a=0，求f(x)的单调区间；

(Ⅱ)若当x≥0时f(x)≥0，求a的取值范围.

解析：第(Ⅰ)问较易.

第(Ⅱ)问，自然的想法是分离参数.

当x≥0时f(x)≥0，即ex-1-x-ax2≥0，ax2≤ex-1-x(x≥0).

但我们发现，沿着这个思路，是不能继续下去的.

再构造函数，令h(x)=ex(x-2)+x+2(x>0)，则h′(x)=(x-1)ex+1.

由于(h′(x))′=xex>0对x∈(0,+∞)恒成立，所以h′(x)在(0,+∞)上为增函数，又h′(0)=0，所以当x∈(0,+∞)时，h′(x)>0，从而知h(x)在(0,+∞)上为增函数.因为h(0)=0，所以当x∈(0,+∞)时，h(x)>0，从而当x∈(0,+∞)时，g′(x)>0，g(x)为(0,+∞)上的增函数，所以g(x)>g(0)，a≤g(0).

问题似乎解决了，可是g(0)无意义，忙碌了半天，徒劳而无功.

问题陷入了僵局，怎么办？

我们将问题作个转换，将“当x≥0时f(x)≥0”换个说法，变为“f(x)在[0,+∞)上的值非负”.

如此一来，不难就此猜想出a的取值范围.

至此，我们可将待证命题转换为如下命题予以证明：

因为转换，我们将高考把关题进行得如此简单！没有转换，我们做什么？

参考文献

[1]吴建山,林新建.自主招生考试数学解题四意识[J].福建中学数学,2014，1-2,14-16.

[2]林新建.数学高考解题的“三化四策八关注”[M].厦门：厦门大学出版社.

*本文是“2015年漳州市基础教育课程与教学研究课题”《国家命题背景下数学高考复习教学的因应策略研究》的研究成果.