直流微电网中不同网络结构的负荷功率分配精度研究

刘一琦，王建赜，傅 裕，李宁宁，纪延超

（哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001）

0 引言

随着传统能源的开发和利用，全球范围内空气污染问题日益严重，人们已经逐渐意识到可再生能源将会在未来能源结构中具有重要比重，同时为了对系统不同类型的绿色能源，如光伏、风电、地热能、生物质能和海洋能等分布式能源进行协调统一管理，学者们提出了微电网的概念并对其进行了深入研究［1-3］。

由于可再生能源的分布式发电具有间歇性和随机性的特点，且可再生能源发电并网运行受到能源位置分布和网络连接方式等诸多因素的影响，系统的稳定运行和功率分配的合理性更为复杂，因此对于微电网中多种网络结构连接的有效控制具有重要的现实意义［4-8］。由于系统中负荷功率是由不同的能源发电端通过输电线路输送到不同的负载，因此提高传输的效率和合理分配能量尤为重要［9-11］。直流微电网同样存在类似于交流系统的负荷功率分配精度问题。由于直流微电网中不存在无功功率，因此分配精度问题主要体现在有功功率上。通常情况下，在对直流微电网进行研究的过程中，往往假设系统尺度较小，因此近似忽略线路阻抗。在此情况下，各本地母线电压彼此近似相等。然而，若直流微电网的尺度增大，则需要考虑线路阻抗的影响，在此情况下，不同网络结构的连接方式和各母线电压的不同取值会对有功负荷的分配精度带来影响。为了降低系统的线路损耗，提高直流电网的整体效率，针对微电网系统中不同变换器之间的功率分配问题，文献［12］提出了改进型下垂控制方法，但此方法在多个端口的直流微电网中应用时通信复杂，需要对所有端口进行通信，同时从多个端口进行通信会造成通信冲突和信号通信传输不稳定。因此本文从以下几方面对直流微电网系统的负荷功率分配和电压跌落问题进行改进。

a.由于微电网系统具有多样化的能源接入，形成复杂的系统网络结构，本文针对系统中典型的放射状结构和网状结构进行深入分析。

b.提出引入相邻变换器间直流电压的平均值和直流侧功率的平均值作为被控对象，以同时补偿直流母线电压跌落和提升负荷分配精度。不同变换器之间电压和功率信息的传输通过低带宽通信网络实现。此方法在具有多个可再生能源输入端的系统中具有通信量小、通信成本低等优点。

c.本文功率型下垂控制自身同时受负载电流和电压两方面的影响，因此对其进行分析需要考虑更多方面的信息。特别是系统中通常会存在功率型负荷，该负荷形式相比传统的电阻性负荷而言更容易降低系统的稳定裕度。最后讨论了线路阻抗取值、低带宽通信延迟以及预期负荷分配比例对上述控制方法稳定性的影响，并通过仿真验证上述方法的作用效果。

1 微电网中传统的下垂控制

1.1 分布式发电的并联运行

微电网系统中，由于各类可再生能源以分布式形式存在，因此各接口变换器之间形成并联结构［13-14］。直流微电网中，分布式发电的网络结构一般分为放射状结构和网状结构两大类，如图1所示。其中，Udci和Idci分别为第i个变换器直流侧公共连接点电压和电流；rij为原边侧和负载侧之间输电线路的等效电阻；idc1为电源侧电流；∑P为负载侧总功率。传统下垂控制方法可以表示为：

其中，为直流侧输出电压的参考值；Udc为直流侧输出电压的实际值；Pdc为直流侧输出功率；m0为下垂系数。

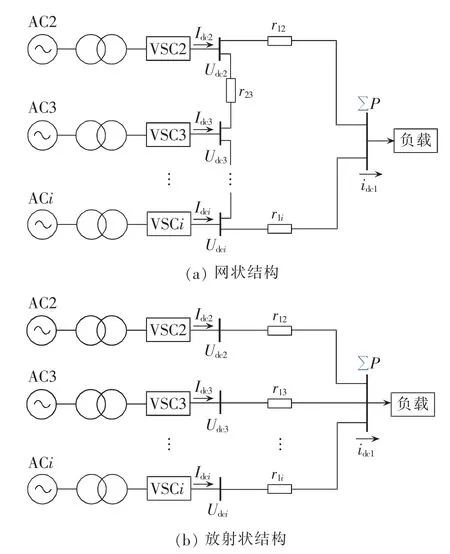
图1 2种分布式发电并网结构Fig.1 Two grid-connecting configurations of distributed generation

1.2 传统下垂控制存在的问题

直流侧下垂控制原理如图2所示。从图2和式（1）可以看出，下垂控制的实现原理在于随着直流侧输出负载功率的增大线性地减小本地直流输出电压的给定值。因此，在传统下垂控制的实现过程中存在2点不足：其一，下垂控制是通过调节直流母线电压的设定值改变变换器输出功率，因此在其实现过程中，不可避免地会引起母线电压上下波动；其二，在直流微电网中，存在负荷功率分配精度问题，由于直流微电网中不存在无功功率，因此分配精度问题主要体现在有功功率上。

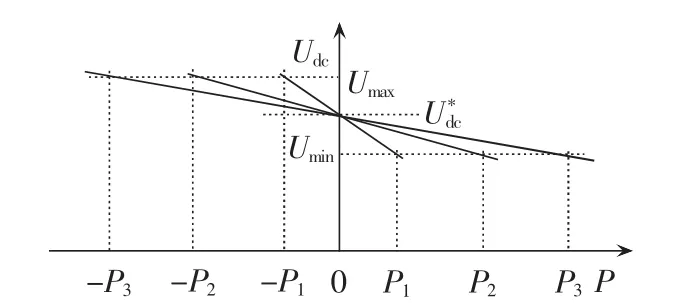
图2 直流侧下垂控制原理Fig.2 Schematic diagram of DC-side droop control

通常情况下，在对直流微电网进行研究的过程中，往往假设系统尺度较小，因此近似忽略线路阻抗。若母线电压近似相等，则有功负荷可以按照所需比例精确分配。然而，若直流微电网的尺度增大，则需要考虑线路阻抗的影响，在此情况下各母线电压的不同取值会对有功负荷的分配精度带来影响。

2 系统不同网络结构下垂控制的问题分析

将图1所示的直流微电网系统的网状结构和放射状结构中的变换器通过戴维南等效电路简化后，直流微电网的等效简化模型如图3所示。

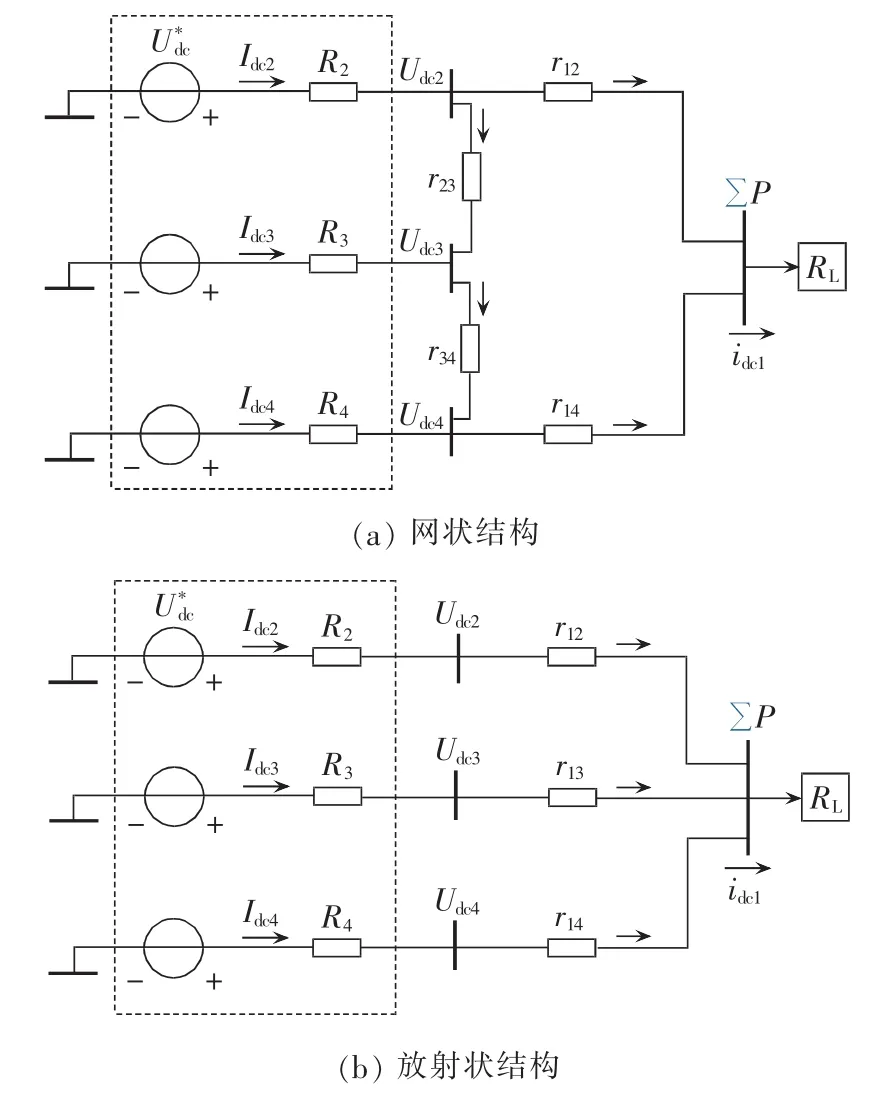
图3 多节点简化模型Fig.3 Multi-node simplified model

通过对系统简化模型中多个电压节点列写的电压、电流方程可推导出网状结构和放射状直流微电网的变换器输出电流如下。

（1）网状结构。

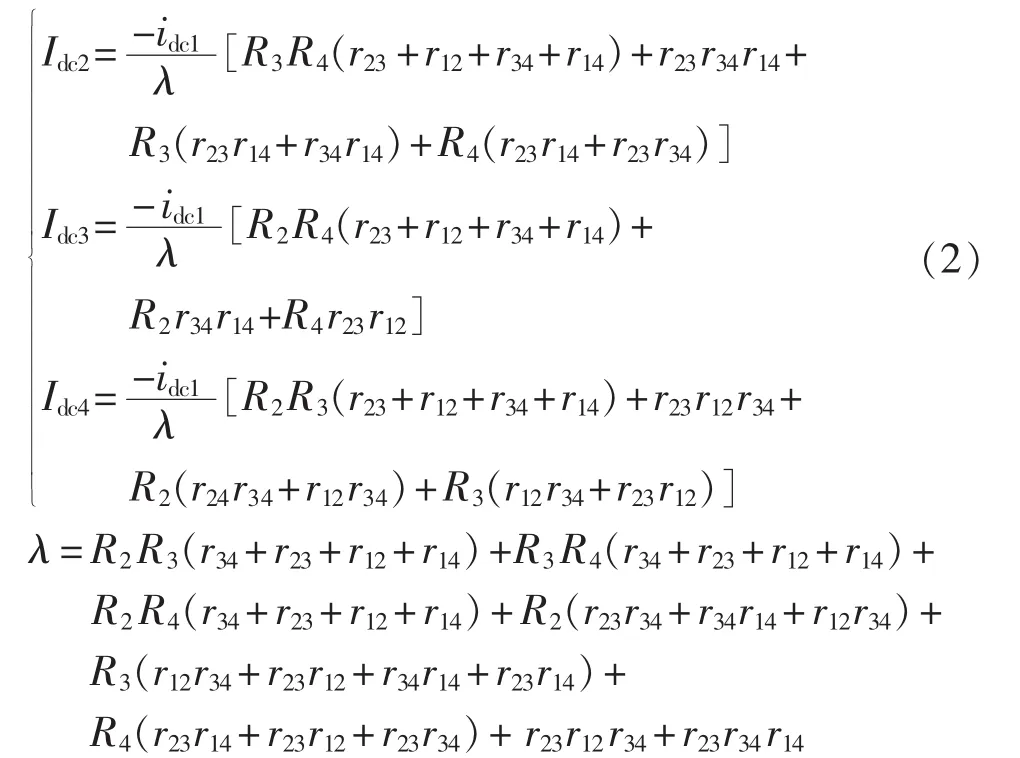
其中，rij（i，j=1，2，…）为不同变换器之间的线路电阻；R2、R3、R4为变换器输出侧的虚拟电阻。

直流微电网中，传统下垂控制只有满足变换器直流侧输出电流与其下垂系数成反比例关系时才可以得到准确的负荷分配精度，如下所示：

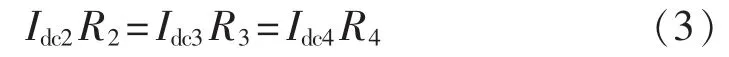
根据式（2）、（3）可知，当下垂系数与线路阻抗之间满足式（3）关系时，负荷精确分配的判定条件为：

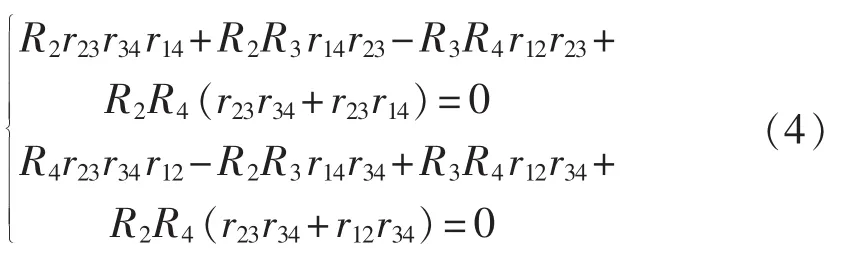
当比例分配为 1∶1∶1，可得：

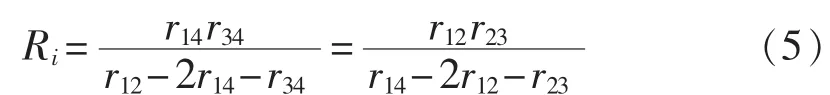
其中，i=2，3，4。

（2）放射状结构。

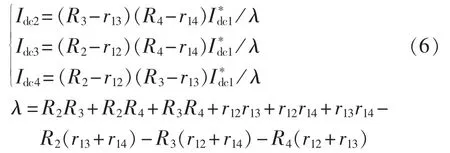
放射状结构功率合理分配判定条件与网状结构相同，因此可得：

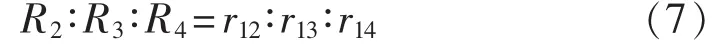
当比例分配为 1∶1∶1 时，可得：

由上述理论推导与分析可知，实际直流微电网系统中，输电线路往往无法保证线路电阻取值精确相等，因此，系统进行下垂控制将不可避免地造成负荷功率分配误差，系统中功率分配不合理也会进一步引起电压跌落或升高。当系统各输电线路电阻严重不平衡时，会导致某个变换器的输出功率超过最大额定容量，从而造成变换器损坏。

3 多节点网络结构控制方法的改进

为了解决传统下垂控制中存在的2个问题，本文提出通过对相邻变换器的直流电压平均值和输出功率平均值进行控制，以补偿下垂控制带来的电压跌落，同时提升负荷功率的分配精度。与已有的针对全局信息进行电压、功率平均的方法相比，改进的控制方法可减小通信强度，进而降低对通信系统的依赖性。相邻两变换器间的直流参考电压如下：

其中，为第i个变换器的输出直流电压参考值；为网侧直流电压参考值；为第i个变换器相邻2个变换器输出电压的平均值；Pdci为第i个变换器输出功率；dci为第i个变换器相邻2个变换器输出功率的平均值；ki为输出功率的比例分配精度；m0为传统下垂控制系数；GLPF为引入下垂控制低通滤波器的传递函数，ωs为低通滤波器截止频率；Gpiv和Gpip为改进下垂控制中补偿项控制器（平均值电压和功率控制器，二者均为传统的比例积分控制器）的传递函数。

在直流微电网的控制系统中，引入低带宽通信系统用于在不同的变换器单元之间传输直流电压和功率取值，通过对其各自的平均值比例积分控制可以消除下垂控制带来的电压跌落；同时还能使得每台变换器中直流电流和其分配比例的比值与其余各个比值的平均值相等，因此可以实现直流输出电流的精确比例分配。但微电网中多个变换器之间包含多种可再生能源的分布式接入，不同接口变换器之间无需高频通信线，并且各自具有独立性，若将所有变换器间传输电压和功率都进行通信采样取值将会引入不必要的误差并增加通信复杂性。因此，本文采用的相邻变换器平均值的方法在计算精度和通信压力上都有很大改善。假设直流微电网系统中变换器个数为n，取全部变换器信号做平均值所需通信次数（Ntotal）与取相邻变换器信号做平均值所需通信次数（Nadjacent）的表达式分别为：

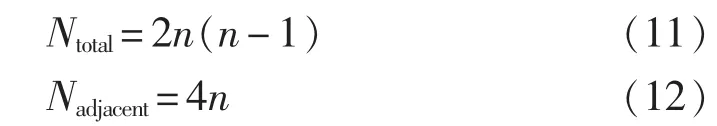
从上述2个公式可以看出，随着变换器台数n的增加，Nadjacent≪Ntotal，因此本文提出的控制方法可以降低通信压力，提高系统运行安全性和实用性，优势明显。同时通过直流功率的平均值控制器也可实现负载功率的粗略比例分配，然后通过外层的控制系统修正分配系统中功率的流动，最终可以实现直流输出功率的精确比例分配。系统的整体控制框图如图4所示。

4 仿真分析

本文通过提出的改进下垂控制方法，利用MATLAB/Simulink对图1中2种结构分别从输电线路电阻rij和通信延迟τ2个方面对控制方法的可行性进行了仿真验证。根据文献［15-16］对直流微电网电压合理选取的论述，本文选取直流侧额定电压为380V。

首先定义不同变换器直流侧的功率和电压的最大值和最小值的差如下［17-18］：

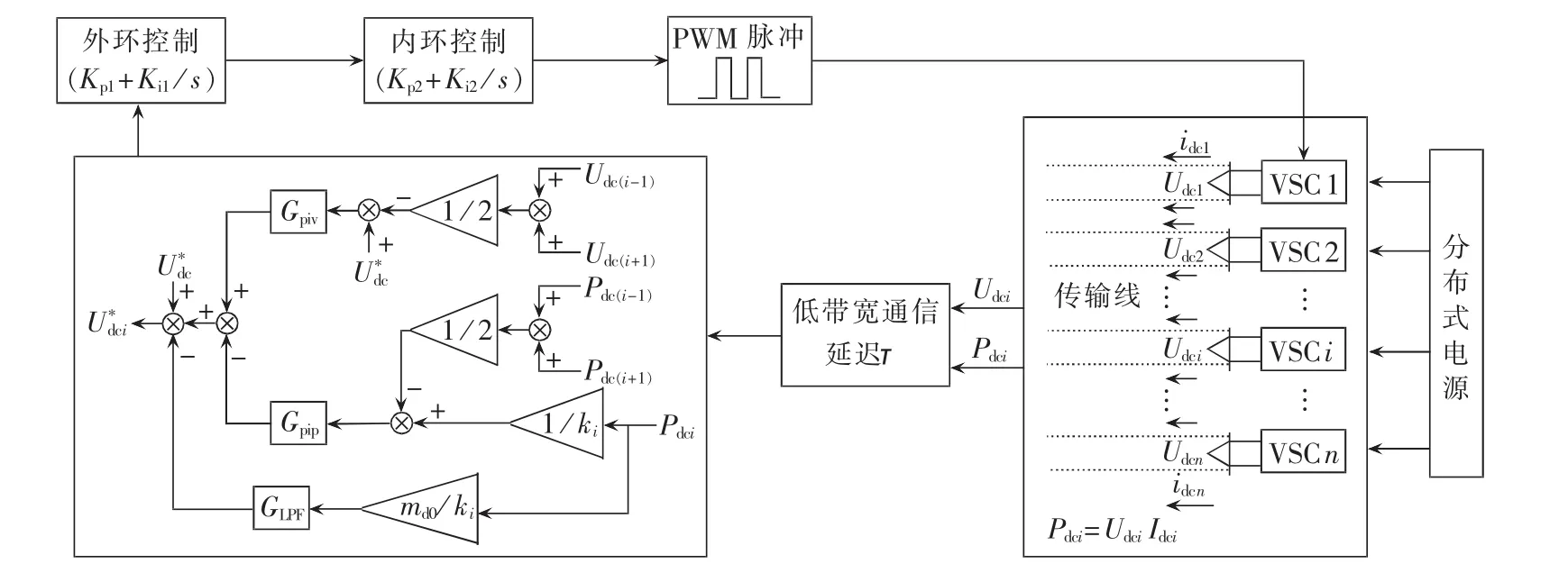
图4 利用改进下垂控制的系统总体控制框图Fig.4 Block diagram of overall system control based on improved droop control

其中，i表示变换器的序号。

下面对直流微电网中网状结构（情况1、情况2和情况3）和放射状结构（情况4、情况5和情况6）分别进行分析。

不同结构的系统参数如下。

情况 1：r12=0.8 Ω，r23=r34=1.2 Ω，r14=1.2 Ω，ki=1，τ=0.1s，仿真结果如图 5（a）所示。

情况 2：r12=0.8 Ω，r23=r34=1.2 Ω，r14=1.2 Ω，ki=1，τ=1s，仿真结果如图 5（b）所示。

情况 3：r12=0.6 Ω，r23=r34=1.2 Ω，r14=1.8 Ω，ki=1，τ=1s，仿真结果如图 5（c）所示。

情况 4：r12=0.8Ω，r13=1.0Ω，r14=1.2Ω，ki=1，τ=0.1s，仿真结果如图 6（a）所示。

情况 5：r12=0.8Ω，r13=1.0Ω，r14=1.2Ω，ki=1，τ=1s，仿真结果如图 6（b）所示。

情况 6：r12=0.6 Ω，r13=1.2Ω，r14=1.8Ω，ki=1，τ=1s，仿真结果如图 6（c）所示。

图5所示为网状结构的直流微电网系统暂态响应仿真结果（Δu为传统下垂控制情况下，变换器直流电压平均值与参考值的差）。由图5（a）和5（b）可知，当t＜1s时，系统只加入传统下垂控制，在线路电阻相同的情况下，通信延迟时间τ分别为0.1 s和1 s时，不同变换器直流侧输出功率最大差值为2530W；当t＞1s时，控制系统中，补偿控制器开启，由于通信延迟时间不同，所以系统中各台变换器输出逐渐趋于设定比例1∶1∶1所需的调节时间不同，但最终达到了等比例分配功率的控制目的；直流侧输出电压达到稳定输出状态，多台变换器直流电压平均值提升到了参考电压水平，最终不同变换器之间最大电压差满足在安全运行范围内。从图5（c）中可知，由于系统中输电线路电阻变化，在0 s＜t＜1s时，系统输出功率差值最大达到了4 176 W，导致系统输出功率不能合理分配，当补偿控制器启动后，尽管线路电阻增大，通信延迟时间也为1s，但变换器输出功率渐渐趋向于设定的控制比例，达到了合理分配的目的，同时电压差值15V也控制在合理的运行范围之内。因此，改进下垂控制适用于网状结构的直流微电网系统。

图6所示为放射状结构的直流微电网系统暂态响应仿真结果。由图 6（a）和 6（b）可知，当 t＜1s时，系统只加入传统下垂控制，通信延迟时间τ分别为0.1s和1 s时，不同变换器直流侧输出功率最大差值为793W；当t＞1s时，控制系统中，补偿控制器开启，由于通信延迟时间不同，所以系统中各台变换器输出逐渐趋于设定比例1∶1∶1所需的调节时间不同，但最终达到了等比例分配功率的控制目的；直流侧输出电压达到稳定输出状态，多台变换器直流电压平均值提升到了参考电压水平，最终不同变换器之间最大电压差不但满足在安全运行范围内，同时与网状结构相比还有所降低。从图6（c）可以看出，在0 s＜t＜1 s时，系统输出功率的最大差值为2156 W，导致系统输出功率不能合理分配，当补偿控制器启动后，变换器输出功率渐渐地趋向于设定的控制比例，达到了合理分配的目的，同时电压差值15.6 V也控制在电网合理的运行范围之内。因此，改进下垂控制也同样适用于放射状结构的直流微电网系统。

表1总结了2种不同结构的系统中不同变换器直流输出功率和电压的最大差值。从2种结构的6种不同情况的对比结果可以看出，加入补偿控制器后输出功率波动很小，满足了比例分配的需要。从物理结构角度讲，输出功率成比例分配和直流母线电压相等这2项控制目标无法同时实现，如在保证功率等比分配的情况下必然会存在电压偏差。这一特点由系统线路压降等固有物理特性决定。本文中所给出的改进下垂控制在保证输出功率达到控制目标的前提下，可以确保输出电压的最大、最小值都在正常电压范围内，并且把输出电压平均值控制为参考电压值，即尽可能地减小了物理系统中固有存在的误差。

图7为2种结构对系统遇到故障情况的暂态响应，当系统中任意一台变换器通信在5s时发生信号丢失故障时，需要获得该控制信号的变换器可以通过采集除此故障变换器外与之距离最为靠近的一台变换器的控制信号，在2个通信延迟0.2 s后获得新的控制信号，控制系统将再次进行调节，达到最终的稳定状态，保证了功率的合理分配和电压稳定运行。

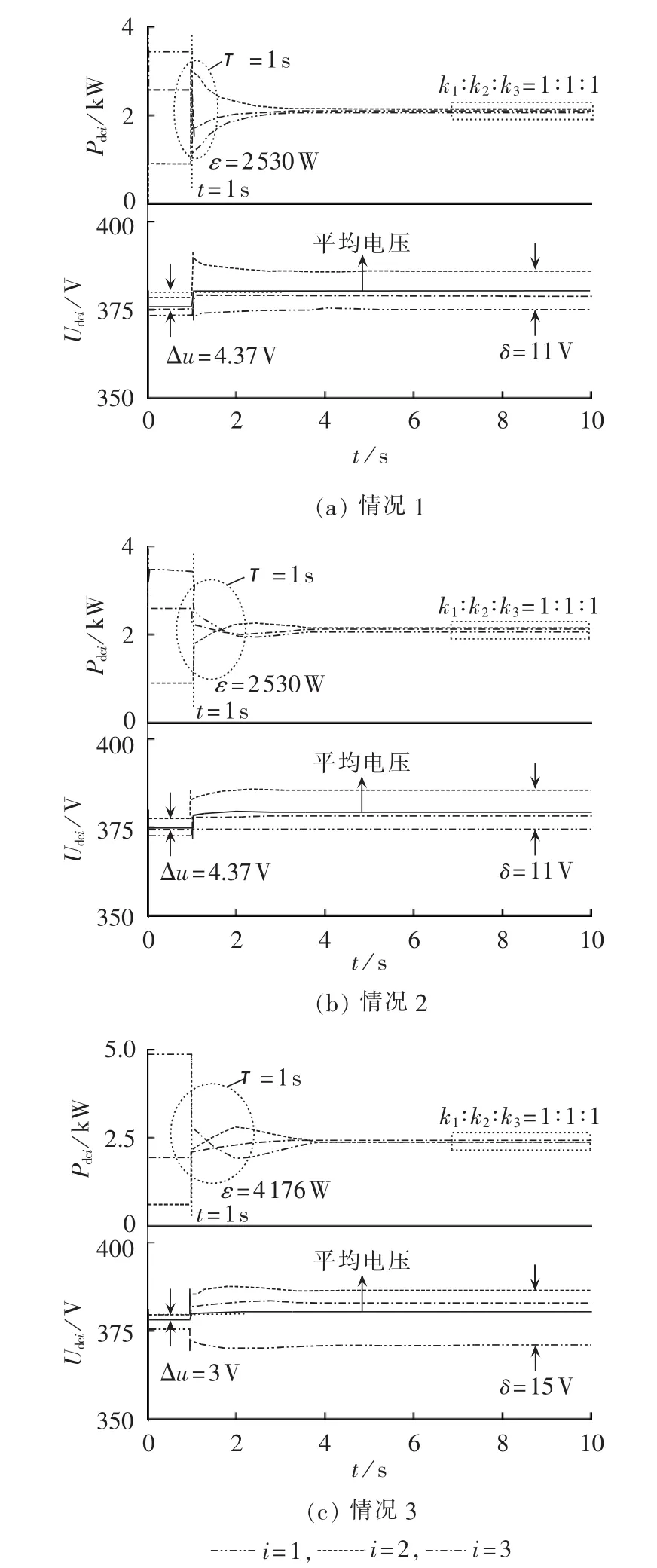
图5 网状结构直流微电网系统暂态响应Fig.5 Transient response of DC microgrid with mesh configuration

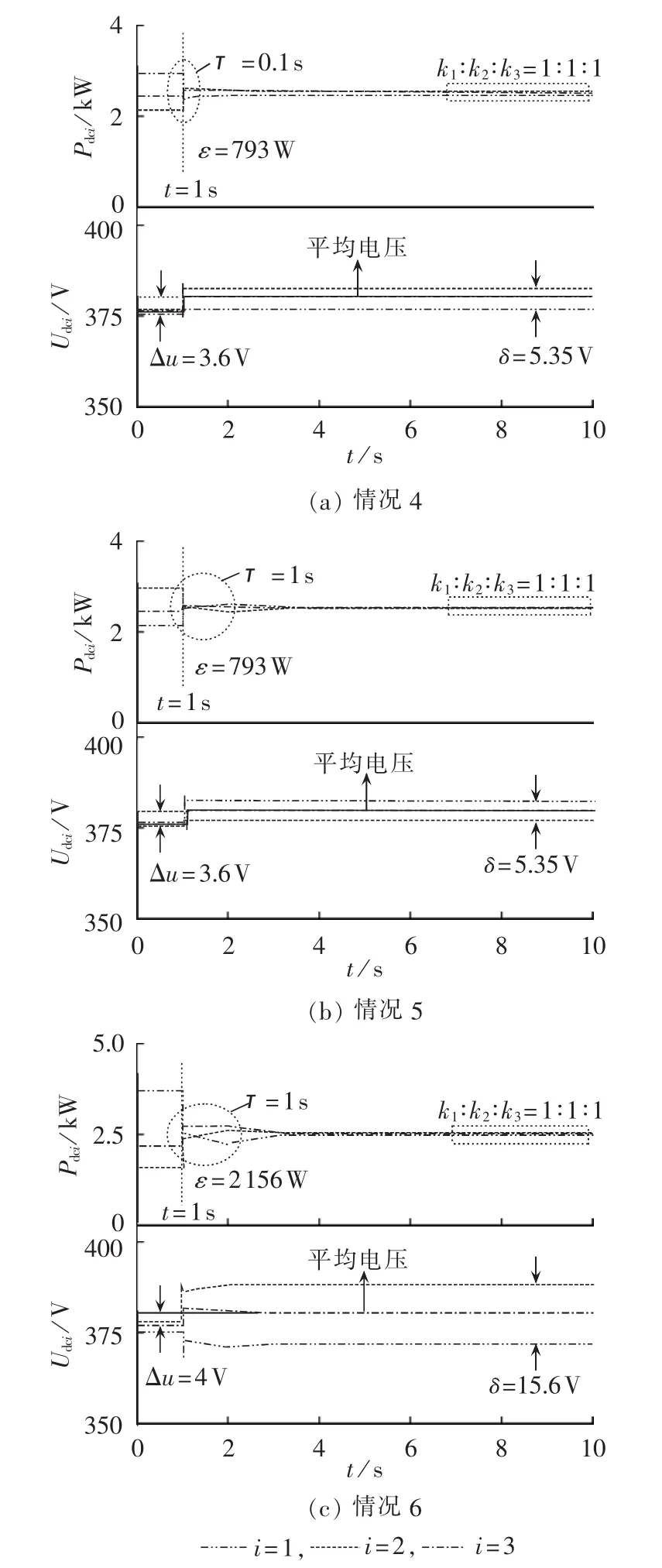
图6 放射状结构直流微电网系统暂态响应Fig.6 Transient response of DC microgrid with radial configuration

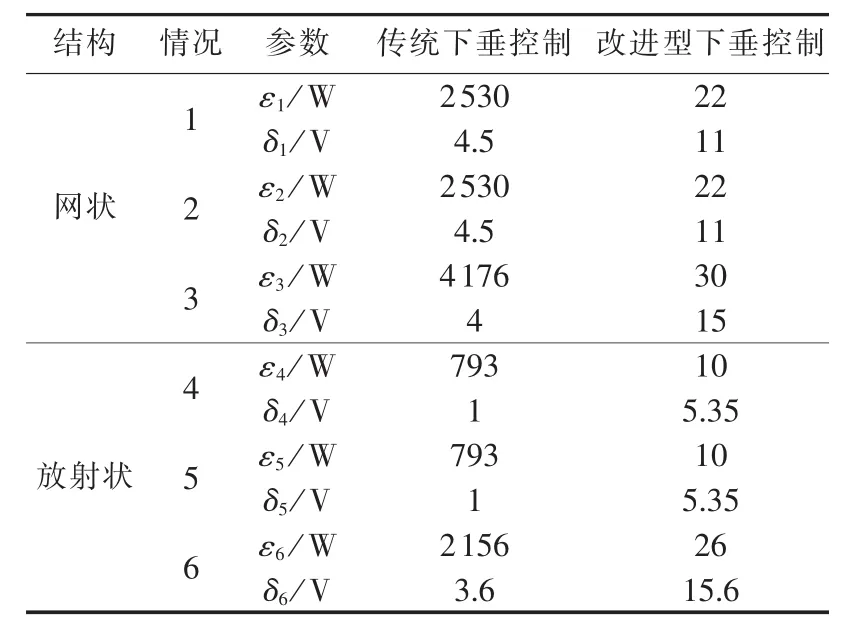
表1 2种结构的仿真结果Table 1 Simulative results of two configurations

图7 2种结构系统故障暂态响应Fig.7 Transient response to fault for two configurations

5 结论

本文以直流微电网为例，对多端口分布式电源的网络结构进行了分析，针对网状和放射状结构提出了一种基于下垂控制的改进功率分配控制方法。该方法采用以目标变换器相邻两变换器的直流侧电压和功率各自的平均值进行控制的思想，同时在本地控制结构中引入直流电压和功率的相邻平均值控制器，一方面补偿下垂控制带来的电压跌落，另一方面考虑了线路电阻不同比值情况下负荷功率的分配精度；同时借助于低带宽通信网络，实现直流侧输出电压和功率采样值在不同变换器单元之间的传输，降低了对通信系统的依赖性。

［1］周稳，戴瑜兴，毕大强，等.交直流混合微电网协同控制策略［J］.电力自动化设备，2015，35（10）：51-57.ZHOU Wen，DAI Yuxing，BI Daqiang，et al.Coordinative control strategy for hybrid AC-DC microgrid ［J］. Electric Power Automation Equipment，2015，35（10）：51-57.

［2］郭力，富晓鹏，李霞林，等.独立交流微网中电池储能与柴油发电机的协调控制［J］. 中国电机工程学报，2012，32（25）：70-78.GUO Li，FU Xiaopeng，LI Xialin，et al.Coordinated control of battery storage and diesel generators in isolated AC microgrid systems［J］.Proceedings of the CSEE，2012，32（25）：70-78.

［3］李玉梅，査晓明，刘飞，等.带恒功率负荷的直流微电网母线电压稳定控制策略［J］. 电力自动化设备，2014，34（8）：57-64.LI Yumei，ZHA Xiaoming，LIU Fei，et al. Stability control strategy for DC microgrid with constant power load［J］.Electric Power Automation Equipment，2014，34（8）：57-64.

［4］张庆海，彭楚武，陈燕东，等.一种微电网多逆变器并联运行控制策略［J］. 中国电机工程学报，2012，32（25）：126-132.ZHANG Qinghai，PENG Chuwu，CHEN Yandong.A control strategy for parallel operation of multi-inverters in microgrid［J］.Proceedings of the CSEE，2012，32（25）：126-132.

［5］冬雷，黄晓江，肖辅荣，等.基于博弈论控制方法的无互联线直流微电网发电系统［J］. 电力自动化设备，2014，34（8）：31-35.DONG Lei，HUANG Xiaojiang，XIAO Furong，etal.Control strategy based on game theory for DC microgrid without wire interconnections［J］.Electric Power Automation Equipment，2014，34（8）：31-35.

［6］阚志忠，张纯江，薛海芬，等.微网中三相逆变器无互连线并联新型下垂控制策略［J］. 中国电机工程学报，2011，31（33）：68-74.KAN Zhizhong，ZHANG Chunjiang，XUE Haifen，et al.A novel droop controlofthree-phase inverters in wireless parallel operation in microgrid［J］.Proceedings of the CSEE，2011，31（33）：68-74.

［7］李玉梅，査晓明，刘飞.含有多个恒功率负荷的多源直流微电网振荡抑制研究［J］. 电力自动化设备，2014，34（3）：40-46.LI Yumei，ZHA Xiaoming，LIU Fei.Oscillation suppression of multi-source DC microgrid with multiple constant-power loads［J］.Electric Power Automation Equipment，2014，34（3）：40-46.

［8］LU X，GUERRERO J M，SUN K，et al.Hierarchical control of parallel AC-DC converter interfaces forhybrid microgrids［J］.IEEE Trans on Smart Grid，2014，5（2）：683-692.

［9］杨忠林，查晓明，孙建军，等.基于反馈线性化的直流微电网全局稳定方法［J］. 电力自动化设备，2015，35（10）：10-14.YANG Zhonglin，ZHA Xiaoming，SUN Jianjun，etal.Global stabilization based on feedback linearization for DC microgrid［J］.Electric Power Automation Equipment，2015，35（10）：10-14.

［10］LI Y W，VILATHGAMUWA D M，LOH P C.Design，analysis，and real-time testing ofa controllerformultibusmicrogrid system［J］.IEEE Trans on Power Electronics，2004，19 （5）：1195-1204.

［11］TAN Sicong，XU Jianxin，PANDA S K.Optimization of distribution network incorporating distributed generators：an integrated approach［J］.IEEE Trans on Power Systems，2013，28（3）：2421-2432.

［12］LU X，GUERRERO J M，SUN K，et al.An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing accuracy［J］.IEEE Trans on Power Electronics，2014，29（4）：1800-1812.

［13］LU X，SUN K，GUERRERO J M，et al.Double-quadrant stateof-charge-based droop controlmethod fordistributed energy storage systems in autonomous DC microgrids［J］.IEEE Trans on Smart Grid，2015，16（1）：147-157.

［14］LI Y W，KAO C N.An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltage multibus microgrid［J］.IEEE Trans on Power Electronics，2009，24（12）：2977-2988.

［15］Emerge Alliance.It’s time to connect with emerge alliance data /telecom center［EB /OL］. ［2015-01-22］.http：∥www.Emergelliance.org /Standards/DataTelecom /Overview.aspx.

［16］WU T F，CHANG C H，LIN L C，et al.DC-bus voltage control with a three-phase bidirectional inverter for DC distribution systems［J］.IEEE Trans on Power Electronics，2013，28（4）：1890-1899.

［17］刘佳易，秦文萍，韩肖清，等.交直流双向功率变换器的改进下垂控制策略［J］. 电网技术，2014，38（2）：304-310.LIU Jiayi，QIN Wenping，HAN Xiaoqing，et al.Control method of interlink-converter in DC microgrid［J］. Power System Technology，2014，38（2）：304-310.

［18］LEE J，HAN B，CHOI N.DC micro-grid operational analysis with detailed simulation model for distributed generation［C］∥2010 IEEE Energy Conversion Congress and Exposition（ECCE）.Atlanta，GA，USA：IEEE，2010：3153-3160.