青年女性乳房表面积预测模型

辛意云， 金娟凤， 蔡倩云， 邹奉元,2

(1. 浙江理工大学 服装学院， 浙江 杭州 310018; 2. 浙江理工大学浙江省服装工程技术研究中心， 浙江 杭州 310018)

青年女性乳房表面积预测模型

辛意云1， 金娟凤1， 蔡倩云1， 邹奉元1,2

(1. 浙江理工大学 服装学院， 浙江 杭州 310018; 2. 浙江理工大学浙江省服装工程技术研究中心， 浙江 杭州 310018)

为建立乳房表面积与文胸制版参数间的量化关系，实验选取在校未孕女青年进行三维人体扫描，利用逆向工程技术定义乳房特征点并提取乳房边界曲线，根据特征点建立乳房局部坐标系，由局部坐标系的横截面与矢状面将乳房表面分割为上内、上外、下内、下外4个区块，并用逆向工程软件分别测量表面积；选取与文胸制版相结合的人体尺寸，利用逐步偏最小二乘回归法，建立各区块乳房表面积与人体尺寸参数间的回归模型。经检验，各区块乳房表面积的原始值与模型预测值间无显著差异，模型均具有理想的预测效果，可为乳房形态分析及文胸个性化定制提供有效的乳房表面积预测方法。

乳房； 逆向工程； 人体尺寸； 偏最小二乘回归； 逐步回归

文胸罩杯的内曲面与乳房表面的匹配程度决定了文胸的穿戴效果。罩杯各部分的形状、面积、位置等应与人体相吻合，且罩杯覆盖的乳房表面积应根据乳房形态及穿戴者的年龄层做出调整[1]，因此，乳房表面积是文胸罩杯结构设计的参考因素之一。

目前针对乳房表面积参数的研究主要集中在医学领域。Catanuto G等[2]根据乳房特征点做出针对乳房的横截面及矢状面将乳房表面分为4个象限，根据每个象限的乳房表面积来分析患者经手术后的乳房形态。Eder M等[3-4]利用Geomagic软件实现三维人体重建，同时根据解剖学定义乳房边缘特征点，由胸高点与乳房边界特征点的连线将乳房表面分为4块，测量并计算左右乳房表面积的差值来评判乳房整形手术患者在术后的双乳对称性，并分析了患者乳房在隆胸手术后6个月期间的变化。综上可得，各区块的乳房表面积为表征乳房形态的重要参数之一。目前许多研究中乳房边界特征点的定义及乳房表面的分割方式适用于医学研究，而难以与文胸罩杯的结构相结合；且乳房表面积作为文胸罩杯结构设计的重要参数之一，其与文胸制版参数间的量化关系有待进一步研究。

本文利用三维人体扫描及逆向工程技术提取乳房边界，分割乳房表面并测量面积；选取与文胸制版相关的人体尺寸，建立基于人体尺寸参数的各区块乳房表面积预测模型。可为乳房形态分析、文胸个性化定制等提供便捷、有效的乳房表面积计算方法。

1 实验部分

1.1 实验对象与仪器

选择18～25岁的在校未孕青年女性作为实验对象，所选样本的乳房轮廓及形态均可由三维人体扫描仪清晰捕捉。

根据样本容量的计算公式

式中置信水平取99% (α=0.01)，正态分布概率U1-α/2=2.58；参考GB/T 1335.2—1997《服装号型女子》中胸围的标准差S=5.5 cm，最大允许误差取高于国家标准(1.5 cm)的△=1 cm[5]，计算得理论样本量N为202人。为防止出现异常值而导致样本的剔除，确定266名样本进行人体扫描。

实验仪器为美国[TC]2三维非接触式人体测量仪。进行人体扫描时，被试者须上身全裸，下身着浅色、贴体的内裤，赤足，头发由浅色浴帽固定；环境温度为(25±3) ℃，相对湿度为(60±10)%，符合裸体测量的环境标准。

1.2 乳房特征点定义及边界曲线提取

在三维人体扫描的基础上，利用逆向工程软件Rapidform进一步处理原始点云。Rapidform可实时将点云数据运算出无接缝的多边形曲面，并具有强大且方便的自由曲线编辑功能。

本文结合Zheng[6]和Lee等[7]在对女性乳房轮廓曲线的研究中提取特征点的方法，提取了22个特征点，如图1所示。

1) 后腰点(WB)：做出人体中心矢状面截面，根据X坐标值(地面坐标系)提取截面曲线上在后腰处最凹的点。

2) 前腰点(WF)：过WB的横截面与人体中心矢状面在前腰的交点。

3) 侧腰点(WS)：根据WB与WF将腰的厚度平分的点。

4) 前腋点(A)：胸与上臂回合所产生夹缝的止点。

5) 乳底点(BU)：对人体做相隔0.5 cm的多矢状面截面，在多条截面曲线的曲率最大处定点，这些点中Y坐标值(地面坐标系)最小的即为BU。

6) 乳房外缘点(BO)：A与WS连线与过BU的横截面线形成交点，A与该交点的中点即为BO。

7) 乳房内缘点(BI)：在过BO的横截面曲线的最凹点两侧提取曲率最大点，即为BI。

8) 乳点(BP)：过BO、BI、BU做参照平面，乳房表面与该参照平面距离最远的点，即为BP。

9) 前颈点(N)：在人体中心矢状面截面曲线上找到前颈最凹的点即为N，方法同WB。

10)I点：从BP点向后对人体做相隔0.5 cm的多冠状面截面，其中第一个连接左、右胸的截面曲线上,在其中心处最低点的两侧提取具有最大曲率的点即为I。

11)B、C点：定义截面E为第一个与体表相交的截面曲线在人体中心处具有1 cm宽、且方向为水平直线的切片。截面E与过N、BP点的截面在体表的相交点即为B；过BP点的矢状面与点A所在的截面相交于C1，与截面E相交于C2，C1与C2的中点即为C。

12) 乳底轮廓线特征点D1～D10：在BO至BU及BU至BI间分别再均匀地各定5个点，方法同BU。

利用样条曲线连结点A、BO、BU、BI、D1～D10、I、B、C即可得到乳房的边界曲线，用于下一步乳房表面积的测量。

1.3 乳房表面分割及表面积测量

多名学者根据乳房特征点做截面或连线来对乳房表面进行分割，并根据各区块的乳房表面积来分析乳房形态[2-4]。为更好地分析人体姿势及局部形态，需建立一个与地面坐标系相关联的局部坐标系[8]。本研究建立了针对乳房的局部坐标系，再根据局部坐标系的横截面与矢状面来分割乳房表面，如图2所示。

局部坐标系的建立方法如下：面1为过BO、BU、BI3点的平面；面2为以BO、BI的连线为法线，且过BP的平面；面3为与其余两面正交且过BP点的面；原点为BP点在面1上的投影。其中，面2与面3为针对乳房的矢状面与横截面，根据这2个截面将乳房表面分为上内、上外、下内、下外4个区块，利用Rapidform软件分别测得面积，并根据左右乳房取均值。

根据局部坐标系做出的乳房横截面及矢状面曲线可与文胸罩杯横向及纵向的分割线相匹配，因此4块乳房表面积在两两相加后可与文胸罩杯的左杯、右杯或上杯、下杯的面积相结合，且4块面积的总和可为1/2、3/4等不同款型罩杯的内曲面表面积提供参考。且4个区块的乳房表面积参数可用于进一步计算得出和值、差值、比值等衍生参数，以满足不同研究的需求。

1.4 人体尺寸的筛选与测量

在实际应用中，为满足制版需求及消费者的易操作性，应使用简单常用且能与文胸样版结合的尺寸参数来对乳房表面积进行换算。

梁素贞等[9]指出文胸设计用的人体尺寸参数包括侧奶杯、前奶杯、上奶杯、下奶杯的垂线距、直线长及弧线长、乳深、乳房钢圈围、乳间距、上胸围、胸围、下胸围及上下胸围差等。

由于在手工测量中, 垂线距及乳深等尺寸无法测得，且乳房除下边缘有自然折痕之外，其余的边界点难以定义，因此本文研究结合实际操作筛选出以下尺寸参数，各尺寸均根据1.2中定义的特征点并由Rapidform软件测量而得。尺寸名称及测量方法如表1所示。

表1 人体尺寸测量项目表Tab.1 Body measurements table

2 数据分析

2.1 测量数据基本统计分析

为确保所测得的乳房面积参数及尺寸参数的可靠性，首先进行奇异值剔除，剔除后剩余248例实验样本。对实验样本测得的各参数进行描述性统计分析，结果如表2所示。

2.2 乳房表面积与尺寸参数间的回归分析

2.2.1 变量设定

为得到4个区块乳房表面积的预测方程，将7个人体尺寸参数作为自变量，设胸围为X1,下胸围为X2，上胸围为X3，上下胸围差为X4，胸点间距为X5，前颈点至胸点距为X6，下奶杯弧线长为X7；4块乳房表面积作为因变量，设上内面积为Y1, 上外面积为Y2, 下内面积为Y3, 下外面积为Y4。

表2 参数描述性统计分析Tab.2 Descriptive statistical analysis of parameters

2.2.2 自变量多重相关性检验

为选择适合的回归方法，首先需检验自变量间是否存在多重相关性。自变量间的相关系数如表3所示，其中有多个相关系数接近1，表明自变量间的相关程度较高。计算自变量间的方差膨胀因子，其结果如表4所示,从中可知，多个自变量的方差膨胀因子大于10，且最大值为37 762。由此说明，自变量间存在高度的多重相关性。

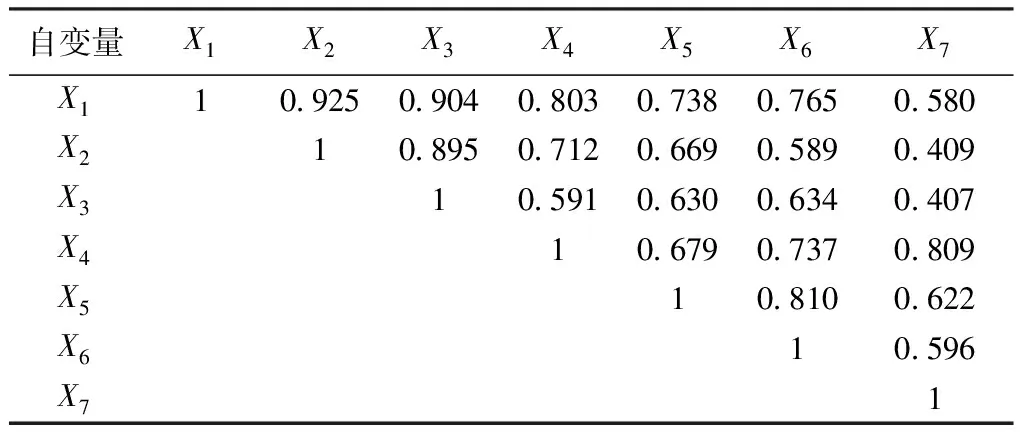
表3 自变量间的相关系数Tab.3 Correlation coefficients among independent variables

表4 自变量间的方差膨胀因子Tab.4 Variance inflation factors among independent variables

2.2.3 各区块乳房表面积回归模型构建

2.2.3.1 回归方法 做出各因变量与各自变量间的散点图。图3示出以下外面积与下奶杯弧线长为例做出的散点图，可见两变量间呈线性关系。根据其余的散点图可判断出因变量与自变量间均呈线性关系。

且由2.2.2可知自变量间存在多重相关性，因此选择逐步偏最小二乘回归分析法，并由MatLab软件编程实现。

偏最小二乘回归分析是主成分分析、典型相关分析和线性回归分析的有机结合，能够在自变量存在严重多重相关性的条件下进行回归建模[9-10]。然而，偏最小二乘的回归模型中包含所有自变量,而自变量偏多时,回归方程将较复杂, 且并非每个自变量都能对因变量有高度的解释作用，因此本文将后退型逐步回归法与偏最小二乘回归法结合，可剔除解释性不强的自变量,得到更简洁精确的回归方程。

即先用所有的自变量构建偏最小二乘回归模型,再依次去除一个自变量,用其余的自变量分别构建偏最小二乘回归模型,根据去除某自变量后回归模型的平均相对误差(EMRE)是否减小来判断是否需删去该自变量，直至模型的EMRE达到最小。

2.2.3.2 回归模型构建及分析 用7个自变量分别对4个因变量进行逐步偏最小二乘回归建模。

在偏最小二乘回归建模过程中，主成分个数及其对因变量的解释能力是影响模型精度的重要因素。本文研究运用交叉验证法来确定最佳主成分个数，即当增加新成分后的交叉有效性大于或等于0.097 5时,认为增加该成分的贡献是显著的[10-11]。最终，经数据的逆标准化处理，得到一般回归方程。4块乳房表面积与人体尺寸参数的回归模型构建及分析如下。

1) 针对上内面积Y1，用所有自变量构建的模型的EMRE为4.23%，依次删去上胸围X3，下胸围X2后的回归模型得到最小EMRE为3.82%；根据剩余的自变量，提取2个主成分时的交叉有效性为0.236 3，提取3个主成分时为-0.644<0.097 5，因此保留2个主成分，且2个主成分对Y1的累计解释能力为0. 932 7。回归方程为

Y1=0.487 1X1+1.117 3X4+3.814 4X5+

3.014 6X6-2.554 2X7-95.777 1

2) 针对上外面积Y2，用所有自变量构建的模型的EMRE为6.07%，依次删去上胸围X3，下胸围X2后的回归模型得到最小EMRE为5.49%；根据剩余的自变量，提取2个主成分时的交叉有效性为0.258 5，提取3个主成分时为-0.721 4，因此保留2个主成分，且2个主成分对Y2的累计解释能力为0. 884 2。回归方程为

Y2=0.555 1X1+2.047 9X4-2.230 7X5+

6.301 7X6-0.863 5X7-77.473 6

3) 针对下内面积Y3，用所有自变量构建的模型的EMRE为3.41%，删去自变量后回归模型的EMRE无下降，因此保留所有自变量；根据所有自变量，提取3个主成分时的交叉有效性为0.357 7，提取4个主成分时为-0.865 1，因此保留3个主成分，且3个主成分对Y3的累计解释能力为0. 954 9。回归方程为

Y3=-0.262 6X1-0.115 5X2+0.342X3-

0.868 8X4+1.551 7X5-0.828 1X6+

8.197 5X7-24.39

4) 针对下外面积Y4，用所有自变量构建的模型的EMRE为5.14%，删去前颈点至胸点距X6后的回归模型得到最小EMRE为4.9%；根据剩余的自变量，提取3个主成分时的交叉有效性为0.269 8，提取4个主成分时为-0.565 9，因此保留3个主成分，且3个主成分对Y4的累计解释能力为0.920 2。回归方程为

Y4=0.250 7X1+0.255X2-0.223X3+0.477 9X4-0.906 8X5+7.853 5X7-25.633 8

根据上述分析，除上外面积回归模型的EMRE为5.49%之外，其余均小于5%，可见回归方程的精度较高；主成分对因变量的累计解释能力均在0.88以上，说明4个回归模型均能高度概括原始数据所携带的信息，且对因变量的解释能力较强。

2.2.4 模型检验

为进一步验证模型的预测效果，再随机抽样20名青年女性作为测试样本，根据各区块乳房表面积的原始值与预测值做配对T检验，结果如表5所示。从中可知，T检验的显著性均大于0.05，表明原始值与预测值之间均无显著差异；且均值的标准误除上外面积为1.074之外，其余均小于1，表明误差较小。

表5 原始值与预测值的配对样本T检验结果Tab.5 Results of paired sample test betweenoriginal values and forecasting values

注：vi1，vi2分别代表原始值与预测值,i=1，2，3，4。

分别绘制4块乳房表面积的原始值和预测值比较图，结果如图4所示。由图可得，原始值和预测值间呈线性趋势，样本点较均匀地分布在斜率为1的直线两侧。

综上可得，4个区块乳房表面积的回归模型均具有理想的预测效果及普适性，可为文胸罩杯结构设计及乳房形态研究提供方便、有效的乳房表面积计算方法。

3 结 论

1) 利用逆向工程技术定义乳房特征点，并在此基础上建立了乳房局部坐标系；根据局部坐标系的横截面及矢状面将乳房表面分割为上内、上外、下内、下外4块，得到各块乳房的表面积。

2) 通过逐步偏最小二乘回归法，建立各区块乳房表面积与人体尺寸参数间的线性回归模型。经验证，模型的平均相对误差均较小，且原始值与预测值间均无显著差异。本文所建模型具有良好的预测效果，可根据与文胸样版相关的人体尺寸参数计算出不同区块乳房的表面积。

FZXB

[1] 陈霞.塑型文胸的结构设计[J].纺织学报,2008,29(1): 94-97. CHEN Xia.Structure design of shaping bra[J].Journal of Textile Research,2008,29(1): 94-97.

[2] CATANUTOG, SPANO A, PENNATI A. Experimental methodology for digital breast shapeanalysis and objective surgical outcomeevaluation[J]. Journal of Plastic, Reconstructive & Aesthetic Surgery, 2008, 61(3):314-318.

[3] EDER M, WALDENFELS F,SICHTERMANN M, et al. Three-dimensional evaluation of breast contour and volume changes following subpectoral augmentation mammaplasty over 6 months[J]. Journal of Plastic, Reconstructive & Aesthetic Surgery, 2011, 64:1152-1160.

[4] EDER M, WALDENFELS F, SWOBODNIK A, et al. Objective breast symmetry evaluation using 3-D surface imaging[J]. The Breast, 2012,21:152-158.

[5] 张文斌，方方. 服装人体功效学[M]. 上海:东华大学出版社，2008:93-94. ZHANG Wenbin, FANG Fang. Apparel Somato-logy[M]. Shanghai: Donghua University Press,2008: 93-94.

[6] ZHENG R. Breast sizing and development of 3D seamless bra[D]. Hongkong: The Hong Kong Polytechnic University, 2006: 80-85.

[7] LEE H Y, HONGA K. Measurement protocol of women′s nude breasts using 3D scanning technique [J]. Applied Ergonomics, 2004,35:353-359.

[8] ZHOU Jie, YU Winnie, NG Sun Pui. Identifying effective design features of commercial sports bras[J]. Textile Research Journal,2013, 83(14):1500-1513.

[9] 梁素贞, 张欣, 陈东升. 文胸结构设计中主要细部尺寸的人体依据[J]. 纺织学报, 2008, 29(12): 69-73. LIANG Suzhen, ZHANG Xin, CHEN Dongsheng. Body foundation of major part-dimensions in bra pattern-design[J]. Journal of Textile Research, 2008, 29(12): 69-73.

[10] 王惠文, 吴载斌, 孟洁.偏最小二乘回归的线性与非线性方法[M].北京:国防工业出版社, 2006:97-123. WANG Huiwen,WU Zaibin, MENG Jie. Partial Least-Squares Regression Linear and Nonlinear Methods[M].Beijing:National Defend Industry Press, 2006: 97-123.

[11] 杨国栋. 基于变量筛选的偏最小二乘回归方法及其应用[D].湖南：中南大学，2013: 22-32. YANG Guodong. A stepwise partial least squares regression method and its application[D]. Hunan: Central South University, 2013: 22-32.

Predicting model of young women′s breast surface area

XIN Yiyun1， JIN Juanfeng1， CAI Qianyun1， ZOU Fengyuan1，2

(1.SchoolofFashionDesign&Engineering,ZhejiangSci-TechUniversity,Hangzhou,Zhejiang310018,China;2.ZhejiangProvincialResearchCenterofClothingEngineeringTechnology,Hangzhou,Zhejiang310018,China)

In order to establish quantitative relationship between breast surface area and bra pattern-making parameters, young non-pregnant female students were scanned by 3-D body scanner, and breast feature points and boundary line were defined and extracted by reverse engineering software, then local breast coordinate system was built based on the feature points. According to the horizontal and segittal plan of local coordinate system, breast surface was divided into 4 parts as upper-inside, upper-outside, lower-inside and lower outside, and surface area of each part was measured. Body measurements related to bra pattern making were selected, regression models between body measurements and surface area of each part were established by the use of stepwise partial least squares regression method. Upon examination, no significant difference exists between the original values and forecasting values of each breast surface area, and all the models have high precision, and can provide efficient breast surface area predicting method for breast shape analysis and bra personalized customization.

breast; reverse engineering; body measurement; partial least squares regression; stepwise regression

2015-09-07

2016-05-19

辛意云(1991—)，女，硕士生。主要研究方向为人体工程与数字化服装。邹奉元，通信作者，E-mail：zfy166@zstu.edu.cn。

10.13475/j.fzxb.20150901606

TS 941.17

A