城市环境Savonius风轮地面效应数值模拟
朱建勇,马树元,王建明,刘沛清
(1.沈阳航空航天大学航空航天工程学部,沈阳 110136;2.北京航空航天大学流体力学教育部重点实验室,北京 100191)
城市环境Savonius风轮地面效应数值模拟
朱建勇1,2,马树元1,王建明1,刘沛清2
(1.沈阳航空航天大学航空航天工程学部,沈阳110136;2.北京航空航天大学流体力学教育部重点实验室,北京100191)
摘要:为了利用城市环境中的风能资源,提出一种卧式安装在屋顶的Savonius风轮。通过数值模拟方法研究Savonius风轮地面效应,研究了间隙比(风轮离地高度H与风轮旋转直径DR的比值)对风轮气动特性的影响,并分析了风轮的雷诺数效应和尾流特性。计算结果表明:地面效应影响风轮的气动特性;在间隙比H/DR=0.4时,风轮的启动性能最优,相比未受地面效应影响的风轮,其扭矩系数和功率系数得到明显的提高,较高功率系数对应的尖速比区间得到拓宽,尾流速度亏损恢复需要更长的距离;雷诺数的增加有助于提高风轮的气动特性。
关键词:风能;Savonius风轮;地面效应;城市环境;建筑屋顶;气动特性;间隙比;雷诺数;数值计算
Project Supported by the National Natural Science Foundation of China(11272034);Natural Science Foundation of Liaoning Province (20102177).
随着风能技术的日益成熟以及城镇化的迅猛发展,人口密集的城市环境成为可用风场,就地利用城市环境风资源,减少城市温室气体排放是发展低碳城市的一个重要途径[1-2]。近年来,国内外对城市环境中的风能利用研究主要集中在以下方面:城市风资源的评估,城市环境具有平均风速低,湍流度较高等空气动力学特点,另外大多数风资源评估方法基于野外大型风电场,准确评估城市风资源具有较大挑战性[3-4];城市风环境模拟,研究不同屋顶外形、不同建筑类型、不同建筑物布置形式对风能增强效果的影响以及确定风力机安装位置[5-7];适于城市环境风力机的选择与设计,由于建筑物的阻挡,在屋顶或墙角边缘迎风方向与水平方向存在一个45°倾斜角,研究表明倾斜来流降低水平轴风力机功率系数,导致风轮的气动载荷不均匀,然而倾斜流有利于提高升力型垂直轴风力机的功率系数[8-10];建筑风能一体化设计,在低碳建筑设计过程中将风力机完美嵌入建筑物中,如巴林世贸大厦在其两翼楼之间沿着高度方向布置三台直径29 m的水平轴风力机[11],我国广州珠江大厦在用于紧急避险的设备层安装垂直轴风力机[12]。
综上所述,水平轴风力机与升力型垂直轴风力机由于其较高的功率系数被更多的研究与应用。然而,以Savonius风轮为代表的阻力型垂直轴风力机尽管功率系数较低,但是因其启动风速低、对湍流度不敏感、尖速比小、气动噪声低,更适合安装在人口密集区域[13]。目前对Savonius风轮的研究主要集中在气动外形的优化以及采用流动控制方法提高其气动特性方面的研究,使其功率系数有了明显提高[14-17]。而城市环境和安装方式等对Savonius风轮气动特性影响的研究较少,尤其是对于安装在屋顶的Savonius风轮,屋顶地面必然对其气动特性造成影响,研究表明安装在屋顶的Savonius风轮的功率系数随着叶片数目的增加而增加,而处于自由流不受地面影响的Savonius风轮的功率系数随着叶片数目的增加而减小[18-19]。因此,有必要深入研究地面对Savonius风轮气动特性影响规律。
本文提出一种适于安装在现有中高层建筑屋顶平台的卧式两叶片Savonius风轮,其旋转轴平行于地面,由于横向安装提高了结构强度,Savonius风轮可以具有更大的横向尺寸,增大风轮的展弦比,减小风轮尖端损失,提高风轮气动特性。由于风轮贴近地面旋转,地面对风轮空气动力的干扰影响风轮的气动特性,导致地面效应的产生。本文利用数值模拟手段研究Savonius风轮地面效应,研究风轮离地高度对风轮气动特性的影响,以及在最佳离地高度下风轮的雷诺数效应和尾流特性。
1 数值计算过程
1.1计算模型与方法
为了提高计算效率,通常选用二维Savonius风轮模型进行数值模拟,已有的研究表明二维数值模拟结果与三维Savonius风轮实验结果相比,二维数值计算结果略高于实验结果,但是变化规律与实验结果一致[20-21]。图1为卧式Savonius风轮横截面示意图,气动外形参数:旋转直径DR=660 mm,偏心距e= 100 mm,叶片直径DB=260 mm。来流方向从左向右;H为风轮旋转过程中最低点距离地面的距离;θ=0°时对应风轮的初始位置,风轮叶片旋转区域包括上半圆区域Ω1以及下半圆区域Ω2,对于图示左侧顺时针旋转的风轮,当叶片处在区域Ω1时称为前进叶片,处在区域Ω2时称为后退叶片,而图示右侧逆时针旋转的风轮,当叶片处在区域Ω2时称为前进叶片,处在区域Ω1时称为后退叶片。由于Savonius风轮的前进叶片作为促使风轮转动的动力叶片,地面对前进叶片气动特性的影响将直接影响Savonius风轮的气动效率,图示右侧风轮前进叶片的旋转区域Ω2距离地面更近,更易受地面的影响,选取图示右侧逆时针旋转的风轮作为本文的计算模型。

图1 风轮旋转方向与离地高度Fig. 1 Rotation direction and ground clearance
由于风轮不规则的几何外形,计算网格采用混合网格,风轮旋转区域为非结构网格,非旋转区域为结构网格,两区域之间通过滑移网格技术模拟风轮的旋转并通过Interface交互面建立流场物理量关系。使用CFD软件求解非定常不可压缩的时均N-S方程,湍流方程标准k-ε二方程模型,采用有限体积法离散上述方程,对流项采用一阶迎风格式,扩散项采用中心差分格式,通过SIMPLE算法耦合压力与速度,数值计算每一时间步长对应风轮旋转0.05°。
以风轮旋转轴心作为计算域的原点建立如图2所示的坐标系。计算域尺寸及边界条件设置:计算域左侧以及上侧距离风轮转轴距离均为10DR,计算域右侧距离风轮转轴距离为30DR;计算域左侧为速度入口,上侧及右侧均为压力出口,下侧及风轮叶片为壁面无滑移边界条件。

图2 计算域与边界条件Fig. 2 Computational domain and boundary condition
1.2计算内容
通常取一个旋转周期的平均静扭矩系数Cts评价风轮的启动性能,取功率系数Cp和扭矩系数Ct随着尖速比λ的变化曲线评价风轮气动特性。功率系数Cp为单位时间内风轮所获得的能量与来流风能之比;扭矩系数Ct为功率系数与尖速比之比,与扭矩成正比;尖速比λ为叶片的叶尖圆周速度与来流风速之比,用来表征风轮旋转速度的快慢。它们的公式如下:

式中:Tsi为第i个相位角对应的静扭矩,Nm;Ti为第i个相位角对应的扭矩,Nm;N为数据采集数目;ω为旋转角速度,rad/s;ρ为空气密度,kg/m3;A为风轮扫掠面积,m2;V∞为来流风速,m/s;RR为风轮旋转半径,m。
计算内容包括:1)在来流风速V∞=3 m/s,计算风轮离地高度H在0.1DR~1.0DR区间内的静扭矩,确定静扭矩最大时对应的离地高度,即为启动性能最优的离地高度;2)在来流风速V∞=10 m/s、15 m/s,计算风轮在最优离地高度对应的气动特性,并揭示雷诺数对其气动特性的影响;3)在来流风速V∞=10 m/s,在最优离地高度时,分析风轮流向的速度恢复系数分布,确定风轮尾迹的影响区域。此外,当H=10DR时默认为风轮不受地面影响,并将该高度对应的计算结果与受地面影响的计算结果进行比较。
2 计算结果分析
2.1启动性能分析
Nakajima M等人对Savonius水轮进行水槽实验,研究水轮的间隙比(水轮距离水底高度与水轮直径的比值H/DR)和旋转方向对其水动力性能的影响,研究表明水轮逆时针旋转时,水轮的间隙比H/DR=0.38时,其水动力性能最优[22]。与本文在风轮间隙比H/ DR=0.4时的启动性能最优的结论是一致的,进而验证了本文数值计算的可靠性。
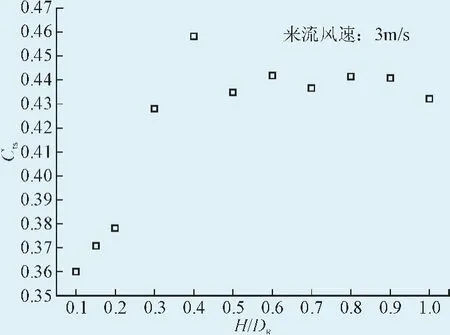
图3 平均静扭矩系数随间隙比变化曲线Fig. 3 Average static torque coefficient versus clearance ratio
上游来流经过风轮时分为a、b、c三股气流,a股气流流经风轮与地面间隙,在前进叶片凸面诱导产生的升力有利于风轮转动;b股气流流入前进叶片凹面产生驻点高压区,然后经偏心间隙流入后退叶片凹面,有助于后退叶片凹面的压力恢复;c股气流流经后退叶片凸面,然后汇入风轮的尾流,在后退叶片产生驻点高压,阻碍风轮的转动。随着间隙比H/DR的增大,流经风轮旋转区域的流量增大,同时三股气流的流量也是不断变化的,共同作用影响风轮的静扭矩。

图4 静扭矩随相位角变化曲线Fig. 4 Static torque versus phase angle
图4为不同间隙比下风轮在0°~360°相位角范围内的静扭矩分布曲线,从图中可以看出,静扭矩变化曲线大致分为3种形态:1)H/DR<0.4,静扭矩最小值在θ=50°、230°,静扭矩最大值在θ=150°、330°;尽管风轮外形每旋转180°为一个循环,但是静扭矩分布不是严格以每隔180°为循环的,主要是由于在较小的间隙比下,地面边界层以及脱落涡在不同的180°循环周期的作用方式不同。静扭矩主要差别在θ=0°、180°左右,主要原因是随着间隙比的增大,作用在风轮旋转区域的流量增大,三股气流流速大,a、b两股气流产生的有利作用大于c股气流的不利作用。2)H/ DR>0.4,静扭矩最小值在θ=80°、260°静扭矩最大值在θ=130°、310°;静扭矩分布每隔180°循环;不同间隙比下静扭矩分布差别不大,地面对三股气流流速的影响逐渐减弱。3)H/DR=0.4,静扭矩分布形态为以上2种分布形态的过渡形态,尽管在该间隙比下静扭矩峰值较小,但是较高静扭矩值对应的相位角范围较大。
2.2气动特性分析
在来流风速V∞=10 m/s,间隙比H/DR=0.4,计算地效作用下风轮的气动特性。图5、图6分别为风轮扭矩系数和功率系数随尖速比的变化曲线。扭矩系数随着尖速比的增大线性减小,且均大于同尖速比下不受地面影响风轮的扭矩系数;功率系数随着尖速比的增大先增大后减小,在尖速比λ=0.7时,功率系数取得最大值Cpmax=0.19,均大于同尖速比下不受地面影响风轮的功率系数,并且较高功率系数对应的尖速比范围得到拓宽。
图7为不同尖速比对应的扭矩随相位角的变化曲线。由图7(a)、图7(b)可以看到间隙比H/DR=0.4、H/DR=10的扭矩变化规律相同,在小尖速比下扭矩较大,波动幅度较小,没有明确的变化规律,当尖速比λ≥0.7,扭矩变化类似正弦曲线,随着尖速比的增大,扭矩波动变大,正扭矩峰值变化较小,负扭矩峰值显著增大。图7(c)为尖速比λ=0.7时间隙比H/DR= 0.4、H/DR=10对应的扭矩随相位角变化分布,间隙比H/DR=0.4对应的扭矩在不同相位角下均得到明显提高。

图5 扭矩系数随尖速比变化曲线Fig. 5 Torque coefficient versus tip speed ratio
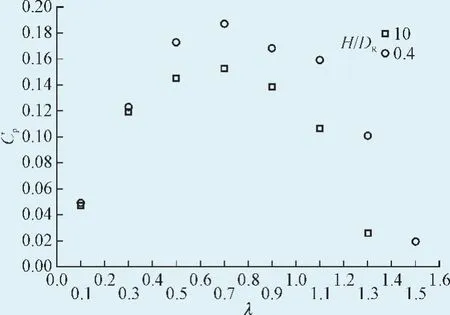
图6 功率系数随尖速比变化曲线Fig. 6 Power coefficient versus tip speed ratio
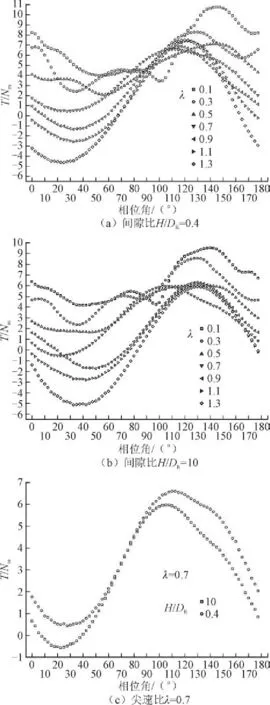
图7 扭矩随相位角变化曲线Fig. 7 Torque versus phase angle
为了验证雷诺数对受地面效应风轮气动特性的影响,在间隙比H/DR=0.4,比较来流风速V∞=10 m/s、V∞=15 m/s风轮的气动特性。雷诺数定义见式(6):
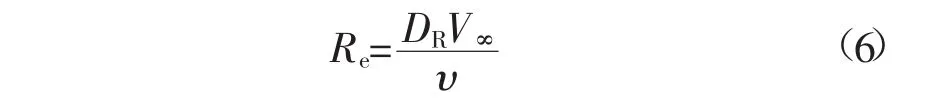
式中:υ为运动黏性系数,m/s2。
来流风速V∞=10 m/s、V∞=15 m/s分别对应雷诺数Re=4.43×105、Re=6.64×105。图8、图9分别为雷诺数对扭矩系数、功率系数的影响曲线。与雷诺数对不受地面效应风轮的影响规律相同,雷诺数的增大有利于提高扭矩系数及功率系数,这主要是由于较高的雷诺数有利于延迟边界层分离。
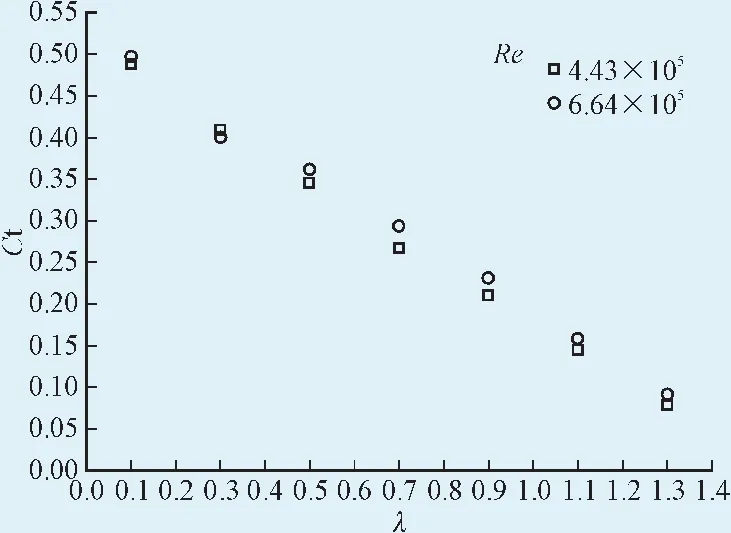
图8 雷诺数对扭矩系数的影响曲线Fig. 8 Influence of Re on the torque coefficient
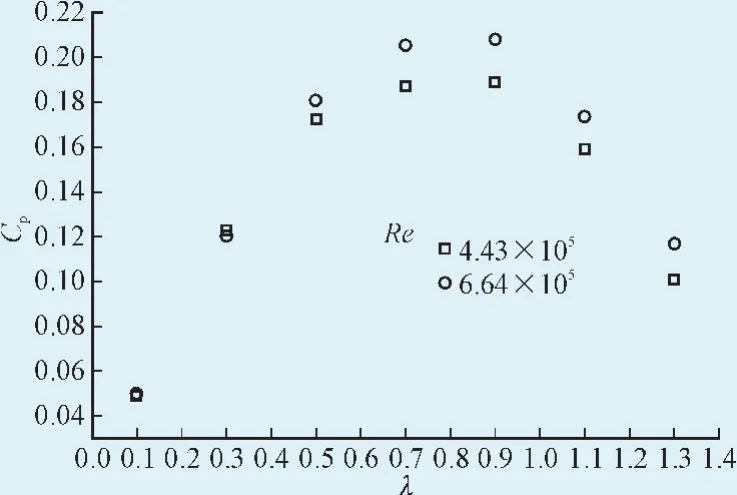
图9 雷诺数对功率系数的影响曲线Fig. 9 Influence of the Re on the power coefficient
2.3尾流特性分析
风轮的安装布置除了考虑城市环境因素的影响,还要考虑风轮尾迹与风轮的相互干扰问题,由于来流条件及风轮本身运行状态的改变导致尾流流场非常复杂。风轮串联布置时,处于尾流区的风轮的输出功率降低。
由于风轮在旋转过程中抽取了风的能量,造成风轮下游的风速降低,称之为尾迹风速亏损。通常利用x方向的速度u与来流速度V∞的比值u/V∞和y方向的速度v与来流速度V∞的比值v/V∞表征尾迹风速亏损。
取来流风速V∞=10 m/s,最佳尖速比λ=0.7的工况,取y=0.5DR、y=0、y=-0.5DR3个不同高度,分析在间隙比H/DR=0.4、H/DR=10时风轮的尾迹区的速度亏损。图10(a)为间隙比H/DR=0.4,相位角θ分别为0°、60°、120°时的u/V变化曲线,随着上游来流接近风轮,u逐渐减小;在风轮旋转区域,由于旋转效应y= -0.5DR对应的u增大并达到峰值,y=0、-0.5DR对应的u减小并取得最小值;在风轮下游流场脱落涡向下游发展,由于粘性的作用,集中涡结构逐渐被耗散,在x=15DR时速度亏损得到恢复,且该截面速度均匀性得到恢复。图10(b)为间隙比H/DR=0.4,相位角θ分别为0°、60°、120°时的v/V变化曲线,在靠近风轮的上游,y=0.5DR对应的v沿y轴正方向增大,y= 0、-0.5DR沿y轴负方向增大,因而上游来流是沿一定的角度方向作用在风轮上;在风轮旋转区域不同高度的v取得峰值;风轮下游尾流区在涡的耗散过程中,v速度分布杂乱无章,在x=15DR时v趋近于零。图10(c)、图10(d)分别为为间隙比H/DR=10,相位角θ分别为0°、60°、120°时的u/V和v/V变化曲线,变化规律与间隙比H/DR=0.4时大致相同,在x=10DR速度亏损得到恢复,相比H/DR=0.4时速度亏损恢复所需要的距离缩短,这主要是没有地面限制,尾流区涡耗散性更大。
3 结论
1)将Savonius风轮安装在中高层建筑屋顶进行风力发电时,需要考虑Savonius风轮的地面效应,即屋顶地面对风轮气动特性的影响。
2)本文提出一种适于城市环境风能利用的卧式Savonius风轮,通过数值模拟得到在风轮安装时,当间隙比为H/DR=0.4时,风轮气动特性最优,在尖速比λ=0.7时,风轮达到最高的功率系数;功率系数随着雷诺数的增大而增大,因此较大尺寸的风轮或较高的来流风速有利于提高风轮的功率系数。
3)通过对卧式Savonius风轮尾迹特性的研究表明,在风轮下游15倍旋转直径时速度亏损得到恢复。因此在屋顶布置Savonius风轮时,下游风轮距离上游风轮的距离不能小于15倍的风轮旋转直径。
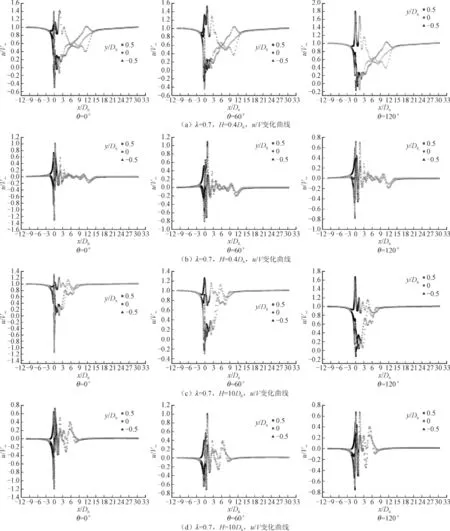
图10 尾迹区风速亏损曲线Fig. 10 Wind velocity loss in the wake region
参考文献
[1] MERTENS S. Wind energy in urban areas concentrator effects for wind turbines close to buildings[J]. Refocus,2002,3(2): 22-24.
[2] DAYAN E. Wind energy in buildings: power generation from wind in the urban environment-where it is needed most[J]. Refocus,2006,7(2): 33-34.
[3]申宽育.中国的风能资源与风力发电[J].西北水电,2010 (1):76-81.SHEN Kuanyu. Wind energy resources and wind power generation in China[J]. Northwest Hydropower,2010(1): 76-81(in Chinese).
[4]黎作武,贺德馨.风能工程中流体力学问题的研究现状与发展[J].力学进展,2013,43(5):472-525. LI Zuowu,HE Dexin. Reviews of fluid dynamics researches in wind energy[J]. Advances in Mechanics,2013,43(5): 472-525(in Chinese).
[5] AYHAN D,SAGLAM S. A technical review of buildingmounted wind power systems and a sample simulation model[J]. Renewable and Sustainable Energy Reviews,2012(16): 1040-1049.
[6]袁行飞,张玉.长方体建筑屋顶风能利用效能研究[J].土木建筑与环境工程,2012,34(3):117-123. YUAN Xingfei,ZHANG Yu. Wind power utilization efficiency on roof of rectangular buildings[J]. Journal of Civil,Architectural & Environmental Engineering,2012,34(3): 117-123(in Chinese).
[7] LEDO L,KOSASIH P B,COOPER P. Roof mounting site analysis for micro -wind turbines[J]. Renewable Energy,2011(36): 1379-1391.
[8] BALDUZZI F,BIANCHINI A,CARNEVALE E A,et al. Feasibility analysis of a darrieus vertical-axis wind turbine installation in the rooftop of a building[J]. Applied Energy,2012(97): 921-929.
[9] MERTENS S,KUIK G V,BUSSEL G V. Performance of an H-Darrieus in the skewed flow on a roof[J]. Journal of Solar Energy Engineering,2003(125): 433-440.
[10] MERTENS S. The energy yield of roof mounted wind turbines[J]. Wind Engineering,2003,27(6): 507-518.
[11] SHARPE T,PROVEN G. Crossflex: concept and early development of a true building integrated wind turbine[J]. Energy and Building,2010(42): 2365-2375.
[12]李秋胜,陈伏彬,黄生洪,等.超高层建筑上实施风力发电可行性研究[J].土木工程学报,2012,45(9):11-19. LI Qiusheng,Chen Fubin,HUANG Shenghong,et al. Feasibility investigations on wind power generation on top of super-tall buildings[J]. China Civil Engineering Journal,2012,45(9):11-19(in Chinese).
[13]朱建勇,屈秋林,刘沛清,等.螺旋式S型风轮气动性能试验研究[J].应用基础与工程科学学报,2015,23(5):1059-1068. ZHU Jianyong,QU Qiulin,Liu Peiqing,et al. Experimental investigation on aerodynamic performance of helical savonius rotor[J]. Journal of Basic Science and Engineering,2015,23(5):1059-1068(in Chinese).
[14] AKWA J V,VIELMO H A,PETRY A P. A review on the performance of savonius wind turbines[J]. Renewable and Sustainable Energy Reviews,2012(16): 3054-3064.
[15] NAKAJIMA M,LIO S,IKEDA T. Performance of doublestep savonius rotor for environmentally friendly hydraulic turbine[J]. Journal of Fluid Science and Technology,2008,3(3): 410-419.
[16]朱建勇,赵万里,刘沛清. S型风力机气动设计[J].电网与清洁能源,2011,27(7):112-147. ZHU Jianyong,ZHAO Wanli,LIU Peiqing. Aerodynamic design of savonius wind turbine[J]. Power System and Clean Energy,2011,27(7): 112-147(in Chinese).
[17]赵振宙,郑源,徐小韵,等.螺旋形S型垂直轴风轮结构优化设计[J].中国电机工程学报,2009,29(26):75-78. ZHAO Zhenzhou,ZHENG Yuan,XU Xiaoyun,et al. Optimum figuration of helix S-type vertical axis wind turbines[J]. Proceedings of the CSEE,2009,29(26): 75-78(in Chinese).
[18] MULLER G,JENTSCH M F,STODDART E. Vertical axis resistance type wind turbines for use in buildings[J]. Renewable Energy,2009(34): 1407-1412.
[19] UZARRAGA-RODRIGUEZ N C,GALLEGOS-MUNÑOZ A,RIESCO ÁVILA J M. Numerical analysis of a rooftop vertical axis wind turbine[C]. Proceedings of the ASME 2011 5th International Conference on Energy Sustainability,Washington,DC,USA,August 7-10,2011.
[20] ALTAN B D,ATILGAN M. An experimental and numerical study on the improvement of the performance of savonius wind rotor[J]. Energy Conversion and Manage -ment,2008(49): 3425-3432.
[21] HORIUCHI K,USHIYAMA I,SEKI K. Straight wing vertical axis wind turbines: A flow analysis[J]. Wind Engineering,2005,29(3): 243-252.
[22] NAKAJIMA M,LIO S,IKEDA T. Performance of savonius rotor for environmentally friendly hydraulic turbine[J]. Journal of Fluid Science and Technology,2008,3(3): 420-429.
朱建勇(1987—),男,博士研究生,主要从事风能利用、应用空气动力学方面的研究。
(编辑徐花荣)
Numerical Simulation of Ground Effect on Savonius Rotor Mounted in the Urban Environment
ZHU Jianyong1,2,MA Shuyuan1,WANG Jianming1,LIU Peiqing2
(1. Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136,China;2. Key Laboratory of Fluid Mechanics,Ministry of Education,Beihang University,Beijing 100191,China)
ABSTRACT:A roof -mounted Savonius -type wind turbine with its rotation axis parallel to the roof ground is presented for utilization of wind energy in urban areas. The Savonius rotor operating in ground effect is investigated numerically. The effect of the clearance ratio and the Reynolds number on the aerodynamic performance of the rotor IS investigated and the Reynolds number effect and wake characteristics are analyzed. The results indicate that,the ground effect affects the aerodynamic performance of the rotor. In contrast with the case without the ground effect,at the clearance of 0.4,the starting performance is optimal,the torque coefficient and power coefficient get improved significantly,the range of the tip speed ratios corresponding to relatively high power coefficients expands and the wind velocity ratio does not recover in the wake of the rotor at 15 times rotation diameter. The aerodynamic performance of the rotor also improves with the increase of the Reynolds number.
KEY WORDS:wind energy;Savonius rotor;ground effect;urban environment;building roofs;aerodynamic performance;clearance ratio;Reynolds number;numerical simulation
作者简介:
收稿日期:2015-10-28。
基金项目:国家自然科学基金(11272034);辽宁省自然科学基金(20102177)。
文章编号:1674- 3814(2016)03- 0127- 07
中图分类号:TK89
文献标志码:A

