基于等值建模的大型光伏电站接入电网后暂态稳定性

周志兵，蒋海军，高辉

（1.国网安徽芜湖县供电有限责任公司，安徽芜湖　241000；2.江苏威信电气科技有限公司，江苏南京　210000；3.南京邮电大学自动化学院，江苏南京　210000）



基于等值建模的大型光伏电站接入电网后暂态稳定性

周志兵1，蒋海军2，高辉3

（1.国网安徽芜湖县供电有限责任公司，安徽芜湖241000；2.江苏威信电气科技有限公司，江苏南京210000；3.南京邮电大学自动化学院，江苏南京210000）

摘要：随着光伏产业的快速发展，研究光伏电站并网仿真模型具有重要意义。建立了适用于西北光伏工程的光伏电池工程实用模型，该模型适用于任意温度T和任意光照强度S。以海西电网2014年底网架和运行方式为基础，深入分析了光伏电站接入后电网暂态稳定特性的变化。结果表明，当光伏电站不具备低电压穿越能力时，会引起海西地区大部分甚至全部光伏电站脱网，但系统能够维持稳定运行；当光伏电站具备低电压穿越能力，能显著降低系统运行风险。

关键词：大型光伏；等值建模；光伏并网；暂态稳定

Project Supported by the National Natural Science Foundation of China（51405244）.

目前，光伏发电主要有并网和离网2种工作方式。由于太阳能电池造价较高，因此光伏发电在过去较多用于偏僻且偏远地区（该地区用户几乎都为离网方式的较小系统）。现阶段，光伏市场及相关产业有了极大发展和进步，已由偏远贫穷地区向中心城市快速发展，太阳能已由能源“补充”逐步变为能源“替代”。同时，光伏发电并网技术进入了一个崭新的发展阶段[1]，开展相关领域的研究是一种必然趋势，具有重要意义[2]。

在电力系统全部电源中，光伏发电方式仍只占据较小的比重，对电网运行并未有显著影响。但是，随着光伏发电自身的发展和国家政策措施的扶持，其在电能供给方面的比重在持续增加，这对电网表现出越来越多的影响[3]：电能质量[4]、电网经济运行及频率控制[5-6]、安全稳定分析[7]、配电网运行分析及控制[8]。文献[9]将逆变器作为核心，遵循其拓扑构成的要求完成等值建模；文献[10]按照光伏发电各元件组成的序列，将各相应的模型（诸如光伏电池、逆变器及最大功率跟踪控制模型等）综合起来完成建模；文献[11-12]基于无损二端口特征构建了2种并网型光伏发电系统的二端口网络模型，即等效无损型和等效有损型；文献[13]根据各受控源给出的电压电流数据，构造了光伏发电的状态模型，为其性能的分析给予了较好的支撑。

随着光伏发电规模的日益扩大，针对光伏发电系统的建模工作已成为光伏发电并网研究的基础。文献[14]利用光伏电池电路的电流方程及电路连接理论，将不同类别的各太阳能电池进行串联，并研究了串列电流特性，分析了各单体电池与总体输出功率的关联性；文献[15-17]针对阴影情况下光伏发电功率的输出特性进行了研究，其中，文献[15]分析了单个太阳能电池板在阴影条件下的状况；文献[16]进一步构建了2个光伏元件在串联模式下的模型；文献[17]基于实际光伏组件应用模型，构建了阴影下光伏发电功率的串联联接数学模型。同时，国内外学者也针对各种影响光伏发电的因素进行了深入的理论研究和有效的方法探讨[18-19]。然而，针对实际运行工况与大型光伏列阵模型的关联性研究仍需要更为深入的开展。文献[20-21]针对考虑并网的光伏模型研究具有重要的借鉴意义。针对该模型可由光伏列阵、逆变装置以及控制模块等若干方面开展研究。针对独立型的光伏发电系统，有必要针对蓄电池模块进行建模。对于集中式的光伏发电系统而言，不但需要考虑到并网运行后对系统电能质量、保护以及经济运行等诸多影响，更要针对大电网安稳分析及经济可靠运行等方面开展更为深入的研究。

目前国内外学者主要研究了光伏发电系统自身建模的情况，较少涉及其并网模型的深入分析。本文基于大型光伏电站的等值建模，推导并建立了针对西北光伏工程的太阳能电池实用化模型。并基于海西电网的实际网络结构及运行方式，分析光伏电站并网后对于全网暂态稳定特性的影响。以严重故障为条件，计算光伏并网后电网的稳定性。

1　光伏电池模型

1.1等效电路

光伏电池的本质是一类能量变换装置，由于其内部结构中的半导材料PN结的“光生伏特效应”，才能够将太阳能变换为电能，其内部结构如图1所示。

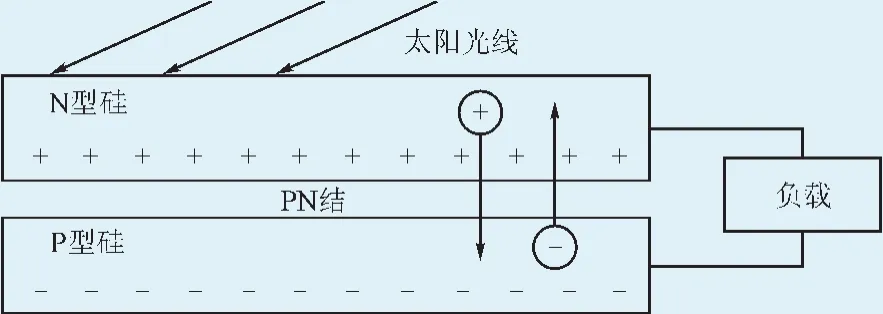
图1　光伏电池的内部原理图Fig. 1 The internal structure diagram of the photovoltaic cell

如果负载与光伏电池连接，则构成了与外部相连的闭环电流，因此实现了功率输出和太阳能到电能的转换，即光生电流。若干光伏电池元件组装后则形成了光伏电池组件，而若干光伏电池组件再进行组合则构成了光伏阵列。单体太阳能电池的等效模型如图2所示。

图2　光伏电池等效电路图Fig. 2 The equivalent circuit diagram of the photovoltaic cell

图2中，Rs为串联阻抗，它表征单体太阳能电池中的各类型电阻的等效阻值；Rsh为旁漏阻抗，它表征单体太阳能电池内部的缺陷或材料边缘的不洁净。

一般而言，光伏电池中Rs的阻抗值非常小，但Rsh的阻抗值非常大，这就导致了串联阻抗的变化对光伏电池能量转换率的影响较大，而旁漏阻抗对该能量转换率则不太敏感。以理想的光伏电池等效模型为例，将不存在串联阻抗及旁漏阻抗，即Rs=0，Rsh=∞。

1.2数学模型

针对光伏并网后的等效模型问题，普遍关心的是在运行环境不同以及太阳能电池本身各异的情况下，太阳能光伏列阵所表现出的综合输入特征。现阶段国内外学者利用电子学理论简化描述硅太阳能电池的等效模型，它是一个I－V非线性特征方程形式，具体表达式为：

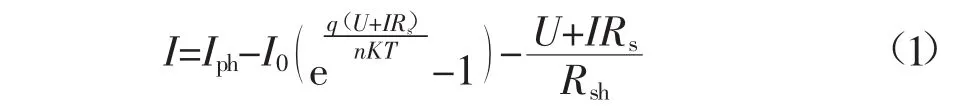
式中：Iph为光生电流，A；I0为二极管的反向饱和电流，A；U为太阳能电池输出电压，V；q为单位电荷，1.6×10-19；K为玻耳兹曼常数1.38×10-23J/K；T为绝对温度，K；n为二极管指数，其中，高电压的输出指数为n=1，低电压的输出指数为n=2。

式（1）给出了具体的光伏电池电流输出表达式，但在光伏电池铭牌参数中一般仅有开路电压、短路电流、最大功率点的负载电流、最大功率点的负载电压等几类参数值，分别表示为Voc、Isc、Im、Um。式（1）的电流表达式中其余参数值均受实际运行环境的影响，不易确定，因此难以广泛应用于工程实践。

由此，采用简化的光伏电池等效模型，具体表达为：

其中，由于旁漏电阻Rsh较大，则（U+I/Rs）/Rsh较小，可以忽略，且正向导通电阻值远大于串联电阻Rs，则使Iph=ISC。

给出边界条件，开路情况下，I=0，U=UOC，且输出功率最大时，U=Um，I=Im，并代入式（2）中可得A、B的表达式为：

由参考日照强度和电池温度情况下的各参数值ISC、UOC、Im及Um，得到最新参考条件下的各参数值，即I′SC、U′OC、I′m及U′m，将其代入式（2）和式（3）中，得到相应的新I－V特性曲线：

式中：Tref为标准电池温度，其值取25℃；Sref为标准日照强度，其值取1 kW/m2；a、b、c可均取经验值，分别为a=0.002 5/℃、a=0.000 5/℃和a=0.002 88/℃。

设T为S、Tair下的光伏电池温度，其中，S为任意光照强度，Tair为任意环境温度，由实验分析得满足工程精度要求的表达式，即：

式中：K可根据实验给定，在工程应用中可取值为K= 0.103（（℃·m2）/W）。

2　并网保护控制模型

通常，并网保护主要分为4类：

1）过流保护。

2）过欠压保护。

3）过欠频保护。

4）三相不平衡保护。

依据光伏并网相关规定可知，大中型光伏发电应能够应对低电压穿越，当并网点存在电压过低情况，可以保证在规定的时间范围内该光伏站无拖网状况。如图3所示给出了相应的控制策略示意图。

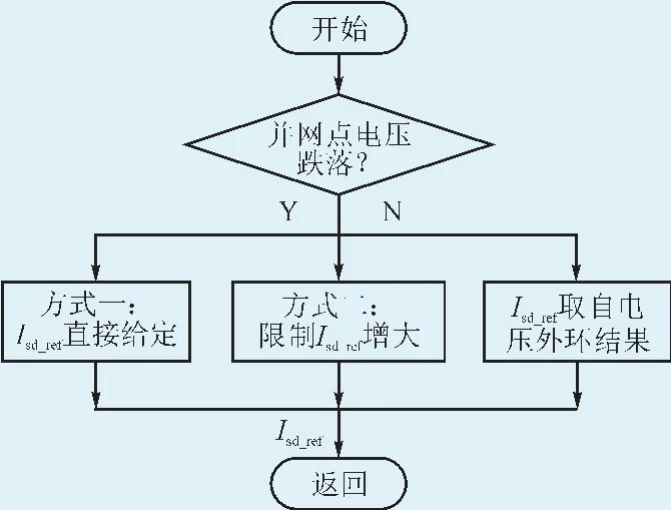
图3　低电压穿越控制策略框图Fig. 3 The diagram of the control strategy for low voltage ride through

图3中对并网点电压数值进行检测，当出现电压跌落时，给定Isd_ref，同时得到Isq_ref，实现无功补偿，提升恢复电压的功能；当未出现电压跌落时，仍利用电压外环获得Isd_ref，同时，可采用Isd数值以限制Isd_ref数值的增长。如图4所示给出了光伏发电系统控制模块的构架体系。由图4可知，光伏并网逆变器的控制模块由直流电压计算、有功和无功功率控制3类基础模块构成。

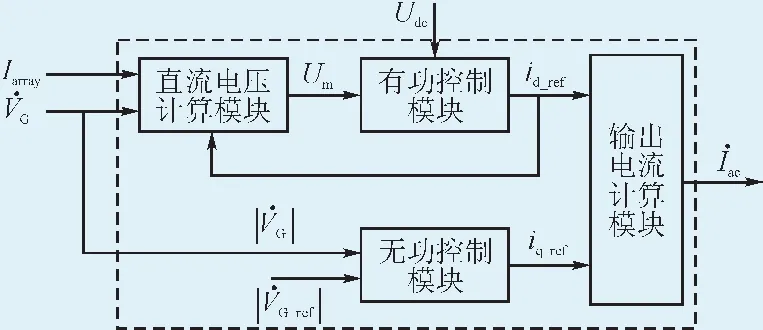
图4　光伏发电系统控制器模型及连接关系Fig. 4 Controller model and connection relationship of photovoltaic power generation system

2.1直流电压计算模块

直流电压计算模块的功能主要为：根据逆变器直流侧电容的模拟数值对直流母线电压进行稳定控制，同时，针对直流输出电能与交流输出电能之间的关联性进行平衡。如图5所示。

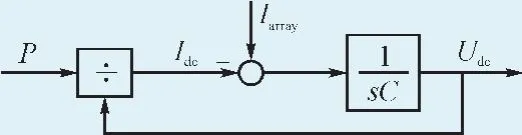
图5　直流电压计算模块Fig. 5 The calculation module of DC voltage

该模块的基本参数为：主要输入Uoc、Xc；其余输入Iarray、p；输出Udc。

2.2有功控制模块

在光伏发电并网点处于最大功率输出点的跟踪电压时，将Udc视为被控量，以其变化量为基础，对id_ref进行计算。该模块主要功能如图6所示。

图6　有功控制模块Fig. 6 The module of active power control

该模块的基本参数为：主要输入Kp_udc、Ti_udc、id_max、id_min；其余输入Um、Udc；输出id_ref。

2.3无功控制模块

无功控制模块利用Q－V下垂模式对并网点电压进行检测，在电压出现跌落时，提供一定比重的光伏发电无功电流，并且对系统故障状态进行模拟及无功支持，如图7所示。

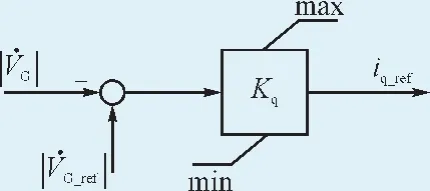
图7　无功控制模块Fig. 7 The module of reactive power control

该模块的基本参数为：主要输入Kq、iq_max、iq_min；其余输入VG_ref、VG；输出iq_ref。

2.4输出电流计算模块

输出电流计算模块中光伏发电输出电流计算表达式为：

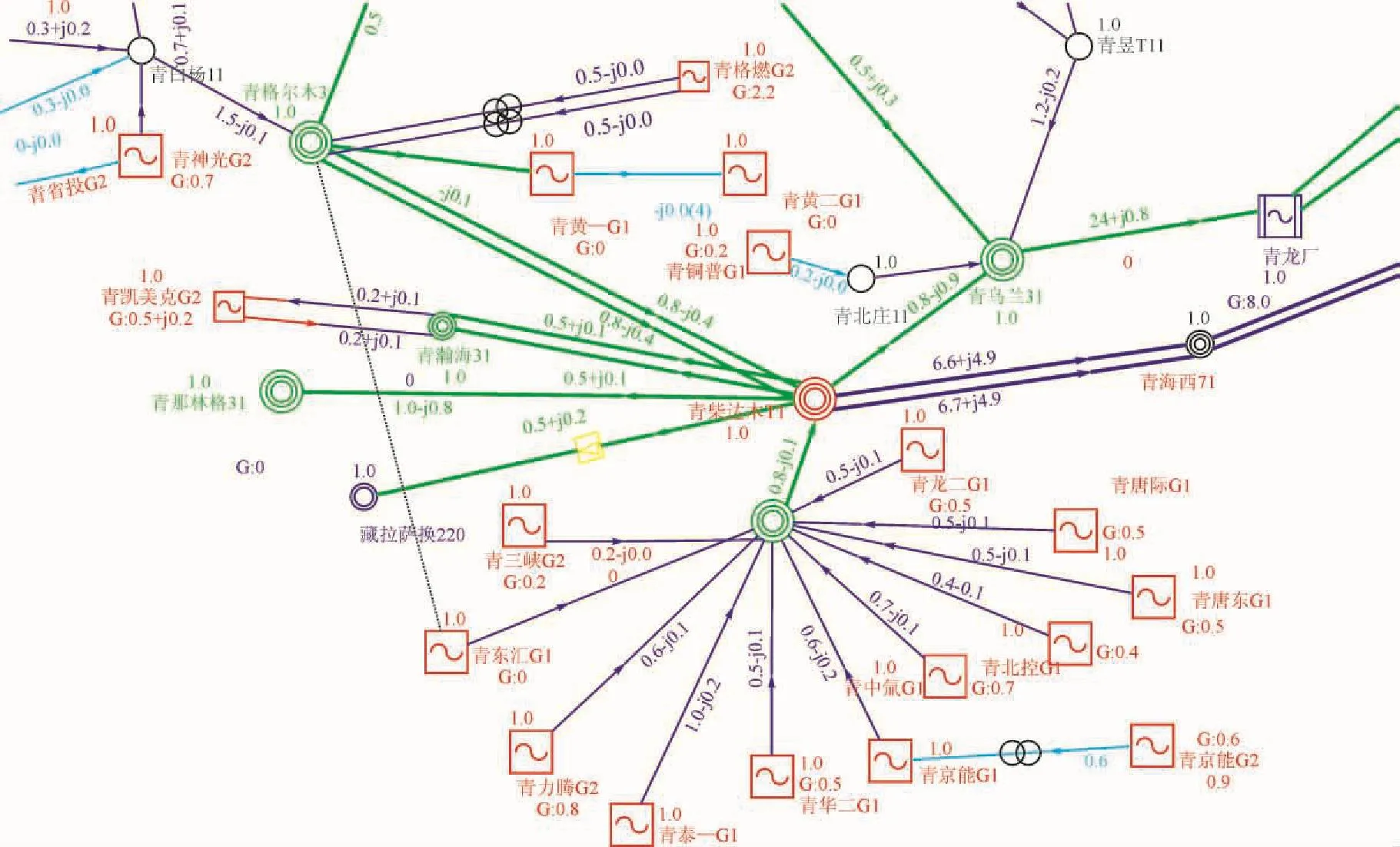
图8　海西电网夏大方式典型潮流图Fig. 8 The typical power flow of Haixi power network in summer

3　仿真分析

3.1边界条件和仿真设置

图5给出了2014年西北电网夏大方式的海西电网典型潮流图。光伏发电系统采用2种方式：

1）不具备低电压穿越能力。根据低电压及过电流保护使得光伏电站保护动作，其中，前者保护为光伏并网点处于额定电压85%以下，时差0.2 s切除故障。

2）具备低电压穿越能力。当出现故障使得光伏并网点电压跌落后，光伏发电系统可以保证在图9给出的范围内，持续正常运行。

仿真故障的故障清除时间如表1所示。

3.2 750 kV输电线路N-1故障后稳定性

西北电网运行方式为格燃2机满发出力290 MW，955 MW光伏电站全接入方式下，发生750 kV柴达木—海西线路N-1故障。假定仿真时间的第1 s在柴达木—海西线的柴达木侧发生三相短路故障，第1.1 s线路保护动作将该故障线路切除。电网发生故障时，光伏电站有、无低电压穿越能力2种情况下的系统功角、电压以及光伏电站送出线的有功功率变化如图10、图11所示。

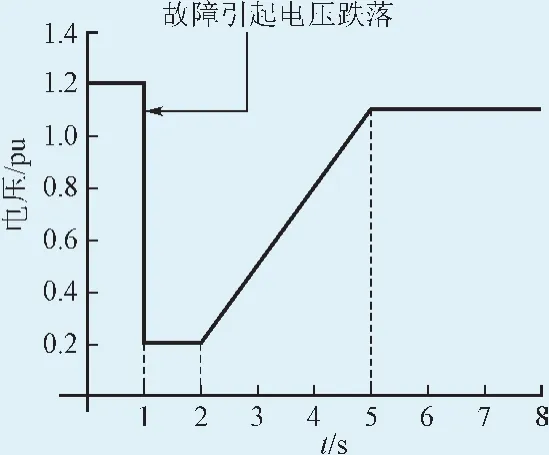
图9　大中型光伏电站低压穿越能力要求Fig. 9 The capability of low voltage ride through of large-and medium-scaled photovoltaic power plants

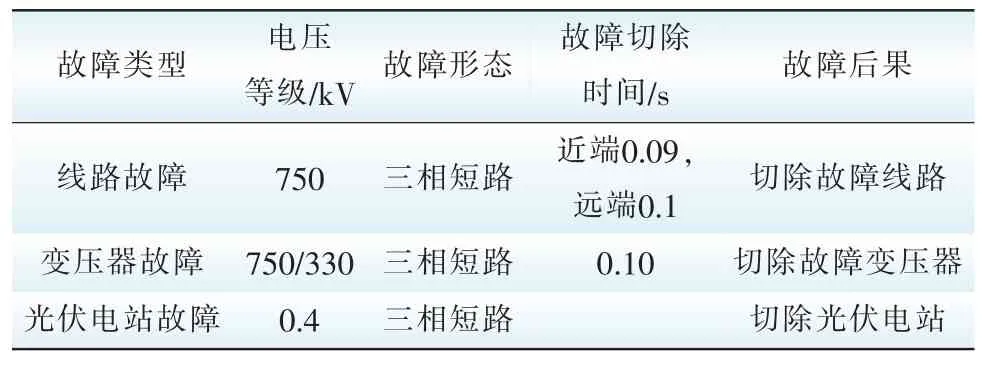
表1　海西电网故障清除时间Tab. 1 The time of the fault clearance in Haixi network

由图11可知，西北电网2014年夏大运行方式下，不论是低压保护动作还是低电压穿越实现，当柴达木—海西线发生三相短路故障时，海西电网主要母线电压的变化规律与光伏电站并网点故障期间变化趋势类似。故障发生后各母线电压都将大幅跌落；常规电厂机组相对功角发生振荡；保护动作将故障线路切除后，海西电网各母线电压将迅速恢复至稳定值，而常规机组的功角的振幅将逐渐减小，并最终趋于稳定。系统均无暂态功角稳定及电压稳定问题。

当柴达木—海西线发生三相短路故障时，若光伏电站无低电压穿越能力，则格尔木地区的共165 MW因低电压动作保护退出运行，光伏电站低压保护动作定值为（0.85 pu，0.2 s），其他光伏电站并网运行。

图10　海西电网的部分低电压保护仿真实验Fig. 10 The low voltage protection simulation results in Haixi network

由图10（d），图11（d）支路青黄河—青乌兰有功功率曲线和图10（e），图11（e）支路青巴音—青德令哈开关站有功功率曲线的对比可知，低压穿越能力能够维持光伏电站的有功出力，提高电力系统的稳定性。以支路青黄河乌兰—青乌兰为例，当柴达木—海西线发生三相短路故障时，电压跌落，无低压穿越能力时，低压保护动作（0.85 pu，0.2 s），光伏电站退出运行，有功出力降为0。当光伏电站具备低压穿越能力，故障发生时，光伏电站有功出力将迅速下跌；故障消除后，迅速恢复到稳定状态，光伏电站保持并网运行。由此可见，具备低压穿越能力更有利于系统电压的恢复和维持系统的稳定运行。

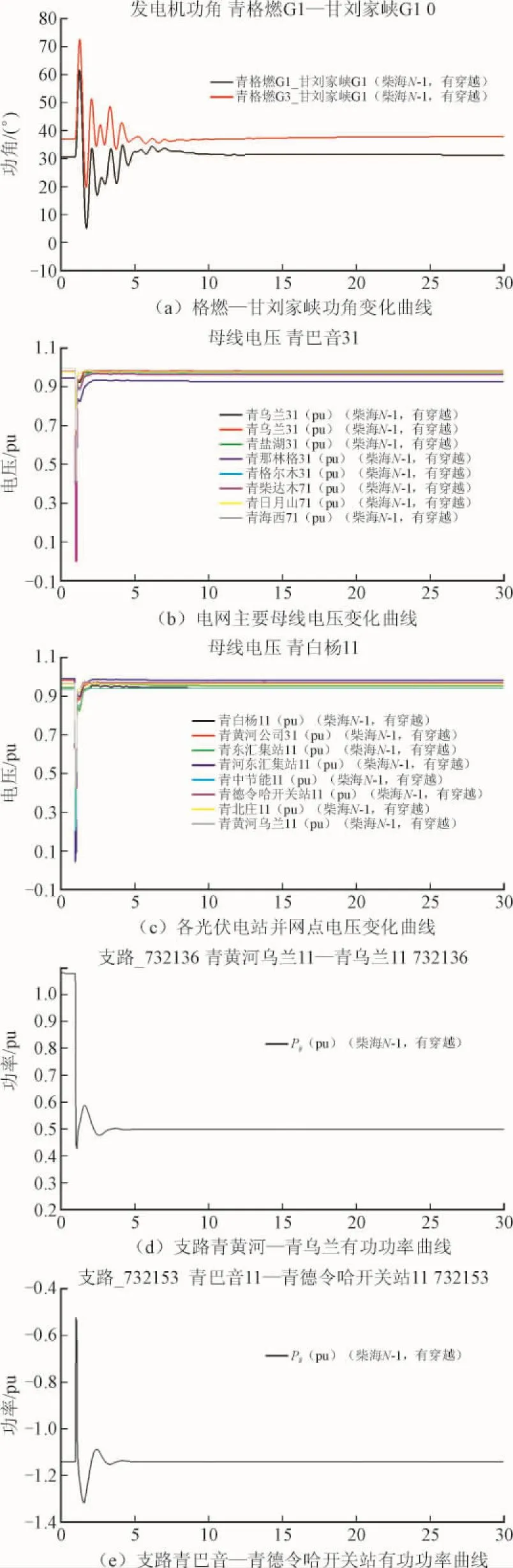
图11　海西电网的部分低压穿越仿真实验图Fig. 11 The low voltage ride-through simulationresults in Haixi network

3.3 750 kV主变N-1故障稳定性

仿真分析以的西北电网运行方式为基础，格燃2机满发出力290 MW，955 MW光伏电站全接入方式下，发生750 kV柴达木主变N-1故障。假定在仿真测试时间第1 s发生故障，故障类型设置为三相短路故障，故障位置位于750 kV柴达木主变压器中压侧，故障切除时间为第1.1 s后线路保护动作。

当系统出现故障后，光伏发电系统按照仿真设置分为具有低电压穿越和不具备低电压穿越能力2类进行分析，图12（a）和图13（a）给出了系统功角变化情况；图12（b）和图13（b）给出了电网中主要节点的电压变化情况；图12（c）和图13（c）给出了光伏发电并网点电压的变化情况；图12（d）和图13（d）给出了2类设置下青黄河—青乌兰线路的有功功率变化情况；图12（e）和图13（e）给出了青巴音—青德令哈站支路的有功功率的变化情况。

由图12、图13可知，在给定的运行方式下，无论光伏电站自身是否具有低电压穿越性能，当发生三相短路的故障时，海西电网主要节点上电压的波动情况和光伏发电系统并网点出现故障时间内的变化情况相似。所有母线上的电压数值在故障出现后都发生了跌落，非光伏电厂的发电机组出现了相对功角的振荡；在故障由保护动作切除后，系统各母线上的电压也快速避免了震荡，恢复到稳定，同时非光伏电厂的发电机组的功角振幅也逐步减少，并恢复到稳定状态。系统未出现电压稳定及暂态功角稳定问题。

当三相短路故障出现在柴达木主变压器时，如果光伏发电系统不具有低压穿越能力，则系统所有的光伏电厂机组（总容量955 MW）由于保护动作而退出运行（低压保护整定值0.85 pu，0.2 s）。由此可见，在出现诸如三相短路故障且光伏系统退运后，在故障切除的情况下相关750 kV母线电压有所降低；同时电网频率在故障切除后也较快恢复，电网继续保持稳定运行。

图12　海西电网的部分低电压保护仿真实验Fig. 12 The low voltage protection simulation results in Haixi network

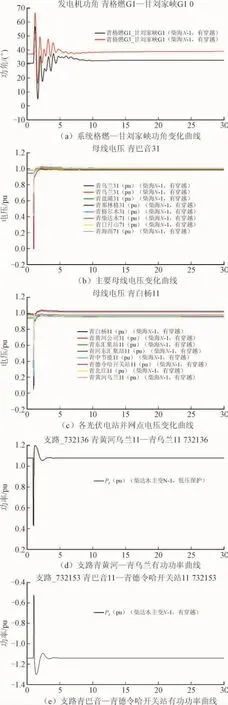
图13　海西电网的部分低电压穿越仿真实验图Fig. 13 The low voltage ride-through simulation results in Haixi network

由图12（d）、图13（d）、图12（e）和图13（e）可知，光伏发电系统的有功输出可以依靠具备低压穿越能力维持。以青黄河乌兰—青乌兰支路为例，在三相短路故障出现在柴达木—海西线时，电压出现跌落，若不具备低压穿越能力，则相应保护动作，所有的光伏电厂机组退运，有功输出功率为0。反之，光伏发电系统有功输出在故障切除后能够快速恢复稳定。如图14所示给出2类情况下电压的比较。

图14　柴达木主变N-1故障下德令哈厂站电压曲线比较Fig. 14 The voltage change curve of Delingha Station when an N-1 failure occurs to Chaidamu main transformer

由图14可知，如果光伏发电系统无低压穿越性能，则光伏电厂的大规模退网将会增加电网电压恢复的难度。同时，为了增强电网抵御大概率事件的性能，减少低电压危害，在大中型光伏电站应具备一定程度的低电压穿越能力。

4　结语

光伏发电的随机性及季节性特征使得其并网运行后对电网造成的不利影响将得到扩大。从光伏发电系统接入电网后对全网的安稳的分析出发，并基于海西电网2014年底拓扑构架及运行方式，详细研究了光伏电站并网后所造成的全网暂态稳定性的情况，当系统出现750 kV线路N-1故障状况时，当光伏发电系统未具备低电压穿越能力时，将造成该地区的多数甚至全部光伏电站与主网解列，但电网仍可以保持稳定运行。在海西电网部分750 kV线路出现N-1故障后，电网都未有电压稳定及暂态功角稳定问题。若光伏发电系统具有低电压穿越能力，将可以明显地降低电网的运行风险。

参考文献

[1] BARNES A K，FAYETTEVILLE A R，BALDA J C，et al. A semi-markov model for control of energy storage in utility grids and microgrids with PV generation[J]. IEEE Trans. Sustainable Energy，2015，6（2）: 546-556.

[2]丁明，王伟胜，王秀丽，等.大规模光伏发电对电力系统影响综述[J].中国电机工程学报，2014，34（1）: 1-13. DING Ming，WANG Weisheng，WANG Xiuli，et al. A review on the effect of large-scale PV generation on power systems[J]. Proceedings of the CSEE，2014，34（1）: 1-13. （in Chinese）.

[3]张雪莉，刘其辉，马会萌，等.光伏电站输出功率影响因素分析[J].电网与清洁能源，2012（5）: 75-81. ZHANG Xueli，LIU Qihui，MA Huimeng，et al. The effect analysis of PV power station output power[J]. Power System and Clean Energy，2012（5）: 75-81（in Chinese）.

[4] VITHAYASRICHAREON P MILLS G，MACGILL I F. Impact of electric vehicles and solar PV on future generation portfolio investment[J]. IEEE Trans. Sustainable Energy，2015，6（3）：899-908.

[5] NAIK R，MOHAN N，ROGERS M，et al．A novel grid interface，optimized for utility-scale applications of photovoltaic，wind-electric，and fuel-cell systems[J]. IEEE Transactions on Power Delivery，1995，10（4）：1920-1926．

[6]汪海宁，苏建徽，张国荣，等.光伏并网发电及无功补偿的统一控制[J].电工技术学报，2005，20（9）: 114-118. WANG Haining，SU Jianhui，ZHANG Guorong，et al. Unitive control of PV grid connected generation and reactive compensation[J]. Transactions of China Electrotechnical Society，2005，20（9）: 114-118（in Chinese）.

[7] VALDERRAMA-BLAVI H，ALONSO C，MARTINEZSALAMERO L，et al. AC-LFR concept applied to modular photovoltaic power conversion chains[J]. IEE Proceedings-Electric Power Applications，2002，149（6）: 441-448.

[8] WANG L，LIN Y H. Dynamic stability analyses of a photovoltaic array connected to a large utility grid[C]// Power Engineering Society Winter Meeting，2000（1）: 476-480.

[9] RODRIGUEZ C，AMARATUNGA G A J. Dynamic stability of grid-connected photovoltaic systems[C]// Power Engineering Society General Meeting，2004: 2193-2199.

[10] MEINHARDT M，CRAMER G，BURGER B，et al. Multi-string-converter with reduced specific costs and enhanced functionality[J]. Solar Energy，2000（69）: 217-227.

[11] TSK K K. A comparative study of maximum power point tracker for photovoltaic panel using switching frequency modulation scheme[J]. IEEE Trans. Industry Election，2004，51（2）: 410-418.

[12] SHERAZ M，ABIDO M A. An efficient MPPT controllerusing differential evolution and neural network[J]. 2012 IEEE International Conf. Power and Energy，2012: 378-383.

[13] KUPERMAN A，AHARON I. Battery and ultracapacitor hybrid for pulsed current loads: a review[J]. IEEE Trans. Sustainable Energy，2011（15）: 981-992.

[14]丁金磊，程晓舫，翟载腾，等.太阳电池模型参数对并联组件输出特性的影响[J].太阳能学报，2007，28（12）: 1312-1316. DING Jinlei，CHENG Xiaofang，ZHAI Zaiteng，et al. Influence of solar cell model parameters on power output of solar PV modules[J]. ACTA Energies Solaris SINICA，2007，28（12）: 1312-1316（in Chinese）.

[15]翟载腾，程晓舫，丁金磊，等.最大功率条件下串联太阳电池电流方程的确定[J].中国电机工程学报，2007，27（14）: 87-90. ZHAI Zaiteng，CHENG Xiaofang，DING Jinlei，et al. Determination of serial solar panels’current equation based on maximum power[J]. Proceedings of CSEE，2007，27（14）: 87-90（in Chinese）.

[16]刘晓艳，祁新梅，郑寿森，等.局部阴影条件下光伏阵列的建模与分析[J].电网技术，2010，34（11）: 192-197. LIU Xiaoyan，QI Xinmei，ZHENG Shousen，et al. Model and analysis of photovoltaic array under partial shading[J]. Power System Technology，2010，34（11）: 192-197（in Chinese）.

[17] LIU Y，WANG H Q，LI P. Adaptive local learning based least square support vector regression with application to online modeling[J]. Journal of Chemical Industry and Engineering，2008，59（8）: 2052-2057.

[18] NARENDRA D K，NALIN K G. Energy yield simulations of interconnected solar PV arrays[J]. IEEE Transactions on Energy Conversion，2003，18（1）: 127-133.

[19] ALONSO M C，RUIZ J M，CHENLO F. Experimental study of mismatch and shading effects in the I-V characteristic of a photovoltaic module[J]. Solar Energy & Solar Cells，2006，90（3）: 329-340.

[20] MEAEN J，ASEMI J M，VOZ C，et a1. Improved equivalent circuit and analytical model for amorphous silicon solar cells and modules[J]. IEEE Trans on Electron Devices，1998，45（2）: 423-429.

[21]赵分县，罗剑波，杨明凯，等.区域安全稳定控制系统在青海西部电网中的应用[J].电力系统自动化，2009 （24）: 91-93. ZHAO Fenxian，LUO Jianbo，YANG Mingkai，et al. Application of regional security of stability control system to westiern power grid of Qinghai[J]. Automation of Electric Power Systems，2009（24）: 91-93（in Chinese）.

周志兵（1983—），男，本科，高工，研究方向为电力系统运行与控制；

蒋海军（1978—），男，本科，高工，研究方向为电力系统机电保护；

高辉（1981—），男，博士，副教授，研究方向为电动汽车与电网互动技术、车载磁悬浮飞轮电池、智能用电等。

（编辑董小兵）

Transient Stability of the Large-Scale Photovoltaic Power Plants Connected to Power Grid Based on Equivalent Model

ZHOU Zhibing1，JIANG Haijun2，GAO Hui3
（1. State Grid Wuhu Power Supply Company，Wuhu 241000，Anhui，China；2. Jiangsu Vision Power Technology Co.，Ltd.，Nanjing 210000，Jiangsu，China；3. Nanjing University of Posts and Telecommunications，Nanjing 210000，Jiangsu，China）

ABSTRACT：With rapid development of the photovoltaic（PV）researches on the model of the grid-connected PV system are increasingly important. In this paper the photovoltaic cell engineering model for PV projects in Northwest China is established and this model is suitable for arbitrary temperature T，arbitrary illumination intensity of S（the supplier can provide the technical parameters. Based on the operating mode and structure of Haixi grid in 2014，this paper presents an in-depth analysis of the power flow characteristics，static voltage and the change of transient stability after the PV plant is connected to the power grid. The results show when photovoltaic power plants do not have the capability of low voltage ride through，most or even all the photovoltaic power plants would be cut off the power grid，however，the system operation still maintains stable. If photovoltaic power plants have low voltage ride through capability，the operating risk can be reduced significantly.

KEY WORDS：large-scale photovoltaic；equivalent modeling；grid interconnection of photovoltaic power；transient stability

作者简介：

收稿日期：2015-11-02。

基金项目：国家自然科学基金项目（51405244）。

文章编号：1674- 3814（2016）03- 0140- 09

中图分类号：TM71

文献标志码：A