卡诺图的一种排列方案

牛文婷（酒泉工贸中专　甘肃酒泉　735000）



卡诺图的一种排列方案

牛文婷
（酒泉工贸中专甘肃酒泉735000）

摘要：根据几何图形对称的特点提出了一种逻辑变量的排列方案，介绍了利用卡诺图的几何对称性快速找出多逻辑变量的逻辑相邻最小项。

关键词：卡诺图 卡诺图的几何对称轴 对称 逻辑反演对称 逻辑变量 逻辑最小项 逻辑相邻最小项

利用卡诺图化简逻辑代数式，直观、简便、易行，其关键是根据逻辑代数式中逻辑变量的个数排列出卡诺图，并能由此排列方案快速地找出逻辑相邻最小项。许多教科书中对此都有较祥细的论述，其排列方案也多种多样。对于多逻辑变量的卡诺图排列，论述较少，一些教科书中采用多个卡诺图排列的方案，概念较多，找相邻逻辑最小项比较麻烦。下面介绍一种多逻辑变量用一个卡诺图排列，并能根据其几何对称性快速找出逻辑相邻最小顶的一种方案。

一、基于几何对称的逻辑变量的排列

1．画卡诺方格图：设某逻辑代数式的逻辑变量数为N，首先确定行、列逻辑变量个数。行逻辑变量个数K可定为（N+1）/2取整，则列逻辑变量个数就为N－K个，卡诺图中每一行有2K个逻辑最小项（即 2K个小方格），每一列有2N－K个逻辑最小项（即 2N－K个小方格）。全图共有2N个逻辑最小项（即2N个小方格）。

2．几何对称轴的概念：从左向右，设竖线为 Y0、Y1、Y2、Y3、……、Y2K。从上向下，设横线为X0、X1、X2、X3、……、X2（N-K）。把全表的纵几何对称轴（只有一条）叫第一级（最高级）纵几何对称轴；第一级纵几何对称轴把全表分成左、右两半，每一半的纵几何对称轴叫作第二级纵几何对称轴（有两个，同时关于第一级对称轴对称）；第一、二级纵几何对称轴把全表分成纵向四个相等的部分，把每一部分的纵几何对称轴叫作第三级纵几何对称轴（有四个，同时关于与其高级的对称轴对称）；……。所有的低级对称轴都关于高级对称轴对称。纵向几何对称轴的总级数等于行逻辑变量数，即纵向有K级。横向同样有N－K级横几何对称轴。第i级纵（或横）几何对称轴的数量为2i-1个。以一维4逻辑变量为例，各级几何对称轴如下图所示（1、2、3、4表示第一、二、三、四级几何对称轴）:

图一

3．由几何对称轴写出逻辑值：当逻辑变量的排列顺序确定以后，如从左向右为ABCD…，A为第一个逻辑变量，B为第二个逻辑变量，……依次类推，同时规定每个逻辑变量的取值从左向右先0后1，A变量关于第一级对称轴反演排列，对称轴左边全部写0，右边全部写1；B变量关于第二级对称轴反演排列，同时关于第一级几何对称轴对称排列；……第i个逻辑变量的值关于第i级对称轴反演排列，同时关于比其高级的对称轴对称排列。依次类推，四变量的逻辑值排列步骤如下：

第一步:写出第一个逻辑变量A的值

图二

4．由各方格行和列对应的逻辑值在方格内写出各方格所代表的逻辑最小项的代表m1号m2、m3、……、mN2。

二、几何对称逻辑最小项与逻辑相邻最小项

按以上方案对各逻辑最小项排列后，任一逻辑最小项关于各级对称轴几何对称的逻辑最小项都是它的逻辑相邻最小项。N个逻辑变量的对称轴级数为N（纵横相加），所以任一逻辑最小项共有N个逻辑相邻最小项。

三、举例

1．四逻辑变量：

（1）卡诺图共有24＝16个方格，排列如图三。设CD为水平方向逻辑变量，则第一个逻辑变量C的值先0后1关于第一级纵几何对称轴Y5反演排列，即Y5左边各项第一位都为0，右边各项第一位都为1；第二个逻辑变量D的值先0后1关于第二级纵几何对称轴Y3反演排列，即Y3左边项第二位为0，右边至Y5之间项第二位为1；比Y3高级的几何对称轴Y5右边各项第二位的值关于Y5左边各项第二位的值对称，依次为1、1、0、0，它们仍然关于第二级对称轴Y7反演对称。

“｜”为第一级几何对称轴，“||”为第二级几何对称轴。同样方法排出列向逻辑变量AB的各逻辑值。根据所写出的各逻辑变量的值，在各方格中写出该方格所代表的逻辑最小项的符号：m1、m2、m3、m4、m5、m6、m7、……、m16。

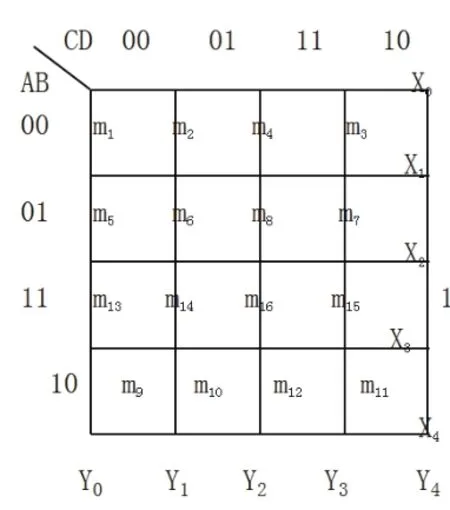
图三

图四

（2）如m1的逻辑相邻最小项为：m3（Y2）、m2（Y1）、m9（X2）、m5（X1）。括号内为m1的几何对称轴。m14的: 逻辑相邻最小项为：m16（Y2）、m13（Y1）、m6（X2）、m10（X3）。

参考文献:

［1］顾德仁等．脉冲与数字电路．［M］北京:高等教育出版社．1984年．

［2］欧阳星明．数字逻辑．［M］武汉:华中科技大学出版社．2000年．

［3］王明臣．脉冲与 数字电路基础．［M］北京:科学技术文献出版社．1991年．

［4］王克义，李洁．电子技术与数字电路．［M］北京:北京大学出版社．1996年．

［5］叶光胜，电工电子技术基础．［M］北京，人民邮电出版社．2009年．

［6］王芳，基于数字电路中卡诺图的应用研究，［J］山西，山西电子技术．2008．6

牛文婷（1983.07），女，甘肃酒泉肃州区人，就职于酒泉工贸中专，主要从事中职学校电工电子线路教 学和研究。

作者简介:

*中图法分类号:TN911

文献标识码:A

文章编号:XJYSD-20160301