魔方与数学

余智麒

摘 要 数学知识和数学思想可以渗透到我们日常生活中的各个方面，甚至是玩乐和游戏中都蕴藏着非常高深的数学思想，魔方正是趣味数学的一种具体体现。本文对魔方进行简单介绍的基础上，重点分析了其中所包含的数学思想和数学知识，最后对我们能从魔方中学习到的数学基本能力进行了介绍。

关键词 魔方 数学 对称

中图分类号：O152.8 文献标识码：A DOI：10.16400/j.cnki.kjdks.2016.12.014

Abstract Mathematical knowledge and mathematical thinking can be penetrated into all aspects of our daily lives， and even the fun and games are bears very advanced mathematics thought， cube is a concrete manifestation of interesting mathematics. In this paper， based on the brief introduction on the focus of one of the cube， the mathematics thought and mathematics knowledge， finally we can learn from the ability of basic mathematical cube are introduced.

Keywords magic； mathematics； symmetric

0 引言

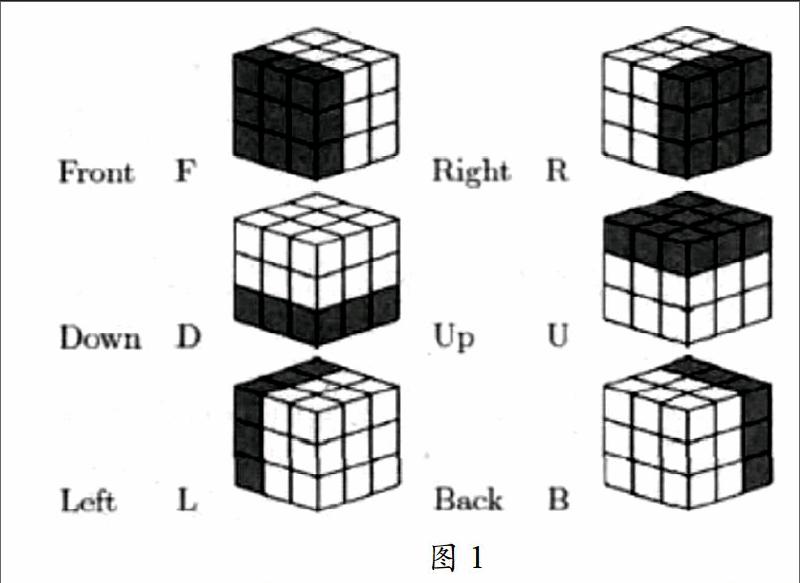
魔方最初是由匈牙利的厄尔诺·鲁比克在1974年最初发明的 ，当时他所发明的魔方是三阶魔方，所谓的三阶魔方也就是指魔方的每个棱有三个方块组成，中心由六个方块组成，整个一有魔方一共有12个棱，8个角块。魔方的各个面如图1所示：

魔方复原的方法已经得到了解决，而且随着魔友越来越多，解法也层出不穷。那么复原一个魔方最少的步骤（“上帝之数”）是多少呢？这个问题困扰了科学家几十年，2010年美国工程师魔方复原的方法已经得到了解决，其结果为20，本文讨论的重点不是上帝魔方复原的方法，而是魔方中所体现的数学问题，以及学习所需要的数学基本能力。

1 魔方中的数学问题

1.1 魔方中的面对称、直线对称和中心对称

所谓镜面对称就是指如果一个集合体被分为两部分，其中一部分是另外一部分关于所给平面的镜面映像，则称该集合体为平面对称，也称为镜面对称。

假如一个集合体上所有的点是关于某一直线对称的，那么该几何体便是关于直线对称的，那么这条直线就称为该几何体的二阶对称轴。假如一个几何体具有二次对称轴，那么该几何体在旋转后能够与自身重合。由此可以推出，如果几何体围绕对称轴旋转后能够与自身重合，则我们称该直线为该几何体为n阶对称轴。

所谓点对称和中心对称也是对称中最为主要的一种对称类型，例如线段AB被点O平分，那么我们称点A，B关于点O中心对称，假如一个几何体中所有的点能够被 点O平分，那么我们称该几何体关于点O中心对称，O被称为对称中心。

下面我就魔方中所包含的对称进行分析。

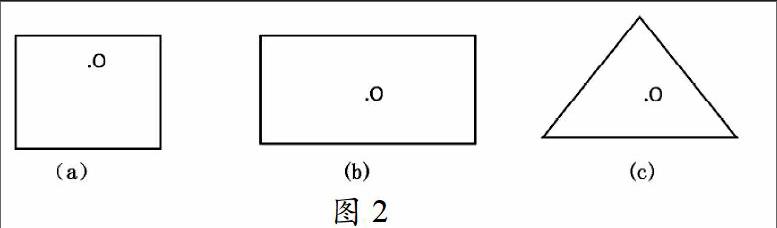
图2所示，图（a）绕旋转轴旋转90度、180度、270度、360度后却不改变其坐标，同理图（b）也可以围绕旋转轴转动180度、360度，图（c）可以绕旋转轴旋转120度、240度、360度，那么图（a）、图（b）、图（c）则分别称为4阶对称轴、2阶对称轴和3阶对称轴。由于正方体中都可以包含上文所说的对称性，因此，3具有阶正方体的魔方同时具备2阶、3阶和4阶对称性，因此，3阶魔方具有其它几何体所不具备的良好对称性。

1.2 魔方中的排列组合原理

根据排列组合公式中的加法原理和乘法原理，三阶魔方的状态一共有种状态。也就是说三阶魔方除过中心 6个固定不变的方块外，剩下的20个方块中，有8个方块放在8个角位置，共有 8！种方法，每个角块有三种方向不同的颜色，因此共有8！€椎？次方种排列，那么，12个棱块就共有12！€？的12次方种排列。但是魔方由于在 还原的过程中不能够将其它方块不动的前提下，单独改变某一方块的方向，也不能之改变某一个棱角的方向，因此，要除去3€？€？。

1.3 魔方中的其他数学问题

例如笔者在某一数学杂志上看到如下一道题目：

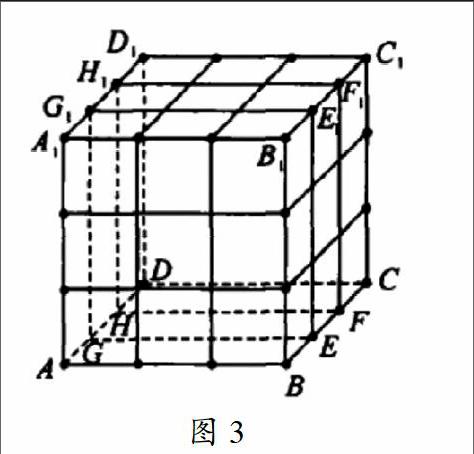
如图3由27个方块组成的魔方，当转动中间层EEIGG，-FF，HHI为a个角度后，那么该魔方的表面积最大值是多少？要解决这个问题，可以从以下方面入手：

首先，我们观察魔方，这个魔方一共有27个立方体，它的表面积假如是54，如果将其中间层转动角度a后，当a=45度时，那么其多出的面积是最多的，那么由此可发现，多出的部分正好是一些等腰三角形，并且这些三角形全等，因此我们可以猜想这时魔方的表面积最大。

如果我们从正视图入手，图4就为两个中心重合的正方形，其边长为4，当将其转动时，则边AD⊥BC，边AD=，DE=，因此，

2 从魔方中能学到的数学能力

2.1 空间想象能力

魔方能够增强学生的空间观念，例如我们可以拿到一个魔方将其上下、左右进行不多方向和不同角度的转动，也可以按照空间坐标轴进行顺时针和逆时针转动，在转动过程中将其用符号或者图形语言记录下来，然后作为魔方还原过称的参考依据，从而增强了学生的空间想象能力。魔方被比克教授发明的直接目的就是为了增强学生的空间想象能力的一种教学工具。我们在学习立体几何时首先要能够在自己的头脑中构建出立体图形，能够将抽象的数学语言具体化和直观化。因此，魔方作为一种典型的立体几何图形，在对其进行复原时某些面不能够被直观地观察到，这时就需要相应的空间想象能力，在头脑中将图形进行分解和组合，从而增强了学习者的空间想象能力。从另一个方面讲，学习魔方公式需要学习者从平面图形开始，那么这样就能够锻炼学习者将平面图形和空间立体图形进行反复比较，从平面图形想象出立体图形，以空间的立体对图形的点、线、面进行研究。

2.2 抽像概括能力

所谓的抽象概括能力就是指学习者能够对现实的客观世界进行积极探索，通过现象研究本质，并且能够将发现的问题用于解决新的问题和做出新的判断的能力，因此，抽象概括能力具体来将就是发现本质和做出判断。

前文提到3阶魔方共有26个小正方体组成，但是其变换可达到4.3€？0种，人们多魔方的复原方法进行积极研究，已经发现了多种复原方法，但是每一种复原方法都必须遵循确定的数学公式和一定的原则，而这些方法都是通过盲解的方式钻研出来的。所谓盲解就是指复原魔方者将眼睛蒙住将事先标号的棱、角快凭借自己的记忆力进行复原。而这种盲解的方式就像我们日常解数学提一样，需要遵循一定的公式和基本定理以及基本原则进行，这一过程可以使得我们从魔方的变换中抽线出其本质规律。因此，这种反复不断的抽象归纳过程以及不断的做出新的判断的过程，从而训练了学习数学必须具备的抽象概括能力。

2.3 推理论证能力

数学中的推理论证能力就是要求学习者根据自己所掌握的数学知识和正确的数学命题来论证另一数学命题的真、假性，这种推理论证的过程就需要归纳法、类比法和演绎法。

当厄尔诺·鲁比克在发明了三阶魔方后，在不长的时间内他又发明了二阶魔方和高阶魔方，直到当代，魔方专家已经发明出了最高的7阶魔方，但是对于初学者来说一般都是从三阶魔方开始，而三阶魔方的学习必须掌握较多的复原公式以及基本的复原原则，通过这些公式和原则的学习，我们就能够将魔方逐渐推广到高阶魔方的复原，而事实上其它高级魔方复原的基本方法都是从三级魔方的推广过程中得到的，那么我们在学习了三级魔方的公式和原则的基础上，想要学习高阶魔方就需要不断地推理和论证，这样逐渐对数学学习所要求的归纳、类比、演绎的基本能力进行锻炼，從而提高学习者的推理论证能力。

参考文献

[1] 秦鸿翼，何传华.魔方，数学趣味的缩影[J].大学指南，2011（4）.

[2] 郑燕.关于初中“魔方与数学”选修课程的设置与实施研究[D].首都师范大学，2008.

[3] 段芳.浅析三界魔方中的数学因素[J].新课程学习：学术教育，2011（7）.