对柯西（Cauchy）不等式启发式教学方式的探讨

杨连青

（阳泉农广校，山西 阳泉045000）

新教材改革要求 “教师主导，学生主体”。如何做才能把这个精神贯彻到整个教学工作的始终？首先是问题情境的创设，也就是说用什么方法、例子，把要讲的中心课题逐渐引出来 （新授课和复习课还不一样，复习课要换个角度思考，对原来学过的题目做变式，最好不要重复，以达到常学常新）。其次要在课堂上对所讲授中心课题分步设置间距，这要因班 （人）而异：基础好、反应快的学生希望间距大一些；基础差、反应慢的学生希望间距小一些。这对教师的主导作用要求较高，备课不但要备教材、备知识，还要备学生。另外就是在课堂上教师要尽量引导学生 （激励学生思维），让学生自己悟出结论，千万不能包办代替。

数学具有高度的抽象性、应用的广泛性和逻辑的严谨性的特点。高度的抽象性是导致数学难学、难教、难懂的主要原因所在。培养学生抽象性思维的水平，要循序渐进，了解每个学生当下具有的思维水平，设置适当的教学问题，不断调整，这是我们广大教师极其艰巨的教学任务之一。对学生思维水平的了解是通过批改作业、课堂反应、课下答疑来逐渐实现的。在讲柯西不等式前，先给学生布置了一道作业题：

例1 已知 x、y、z∈R＋，x＋y＋z＝1，求证：＋

有一位学生给出了如下证明：

这个证法比较好！疑问是为什么要加9x，9y，9z呢？课堂上，先把这个证法告知大家，又把例1做了改动：

例2 已知、y、z∈R＋，且 x＋y＋z＝3，求证：

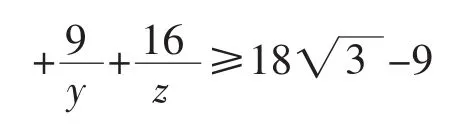
许多同学都认为再加9x，9y，9z肯定证不出来，那应该加几？有的同学这样想：

三式相加整理有：

例3 已知 x、y、z、a、b、c∈R+，且 x+y+z=k，求证：

按例2的待定系数法，大多数学生找到了λ=

再下来列出柯西 （Cauchy）不等式：

例4 已知 a，b∈R （i＝1，2，…n），求证：

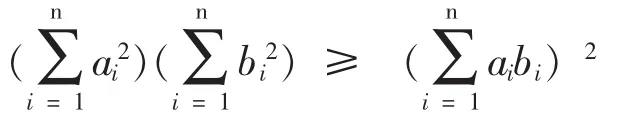
我们把结论改一下：a12＋a22＋…＋an2≥（此时要求bi不全为0）。

这样我们就可以用例1、例2、例3的思路来证本题。

证：由不等式 a2＋b2≥2ab （a，b∈R ） 有：

再将上面n个式子相加有：

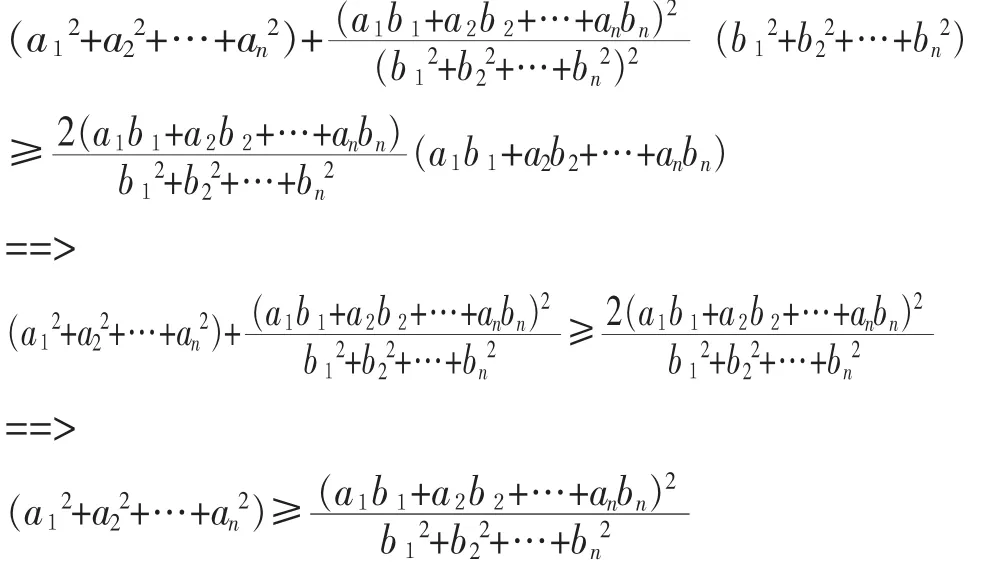
（当 ai=λbi，i=1,2，…，n 时取等号）。

当bi全为0时，原不等式左=右成立。

证毕。

下面，我们换个角度来证明柯西不等式，先看课本的练习题。

例5 a1，a2，b1，b2均为实数，求证：（a12＋a22）（b12＋b22）≥（a1b1＋a2b2）2

大多数学生采用：左边-右边≥0方法。

然后接着讲，若证 （a12＋a22＋a32）（b12＋b22+b32）≥（a1b1＋a2b2+a3b3）2（ai，bi∈R，i=1，2，3）。

当然用 “左边-右边≥0”的方法也可以，只是较例5麻烦一些！再深入证

（a12＋a22＋a32＋a42）（b12＋b22+b32+b42） ≥（a1b1＋a2b2+a3b3+a4b4）2，

甚至证 （a12＋a22＋…＋an2）（b12＋b22+…+bn2） ≥（a1b1＋a2b2+…+anbn）2。

要用 “左边-右边≥0”的方法就太繁了，甚至不可能！还有没有别的构造法了？随后教师提示用一元二次函数 f（x）＝ax2＋bx＋c（a≠0） 的理论来构造证明柯西不等式。对柯西 （Cauchy）不等式来讲，a＝？，b＝？，c＝？ ……（停顿），也就是说要用来代替a，b，c每位学生都做了尝试，有的学生列出了 f （x）＝（a12＋a22＋…＋an2）x2＋（a1b1＋a2b2+…+anbn）x＋（b12＋b22+…+bn2）。 随后再提示：在x系数前乘以2是否更好？

每位学生都列出了：

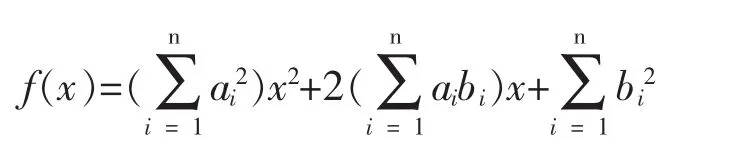
让同学们进行演算，大多数学生得出了

用向量的数量积证明柯西不等式。

在开始讲授柯西不等式之前，有的学生提前预习了该内容，于是提出我们应该从哪里下手？我们能做什么？老师让我们这样做有什么好处？这正像波利亚在他的 《怎样解题》一书中提出的问题，进行“反思、总结”是每个学习者必须经历的一个过程。

柯西 (cauchy)不等式的应用。

作业题 1.若 a，b，c∈R＋，且 a，b，c＝1，

第二堂课对上述两道作业题做了解疑，由学生提问，教师答疑。

作业1.关键是把条件a+b+c＝1用上。有的学生说，满足a+b+c＝1,且a=b=c时取最小值即a=b=时原式取最小值该填空题正好碰对了，若是解答题，就不知道了。

有的学生这样解答的：

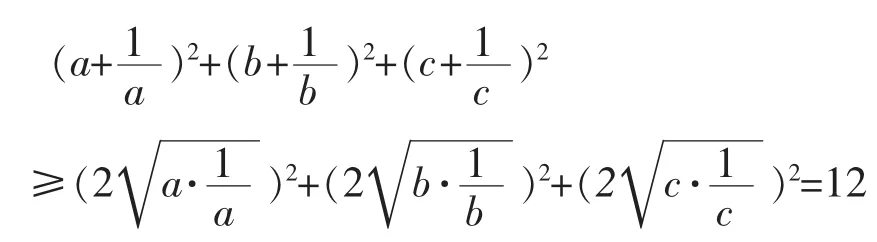
老师问：等式成立的条件是什么？

这个等式成立的条件是a=b=c=1，与原条件a+b+c=1不符！

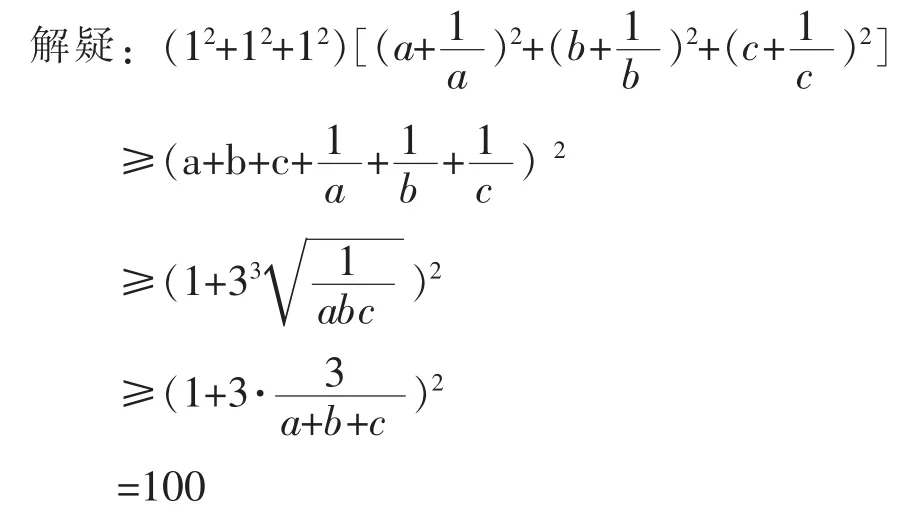
有的同学提出这样的解：

作业2.属竞赛范畴第二堂课没有学生完全解出来！大多数学生只提出了一些思路。本题关键是△ABC内心。

解：设O是△ABC的内心，则

由已知条件有：

49[（b+c-a）2+4（c+a-b）2+9（a+b-c）2]

=36（a+b+c）2……(1)

设 d＝b+c-a，e＝c+a-b，f＝a+b-c（49＝62＋32＋22）

由柯西不等式：

（62＋32＋22）[d2+（2e）2+（3f）2]

≥（6d+3×2e+2×3f）2=36（a+b+c）2

等式成立的条件是：

b+c-a＝9（a+b-c）＝4（c+a-b）

＝＞5a＋4b＝5c，5a＋3c＝5b＝＞a＝13k，b＝40k，c＝45k.

取k＝1就得到满足条件的最小正整数。即a＝13，b＝40，c＝45

注：（1）式可变为 13d2+160e2+405f2-72（de+ef+fd）=0

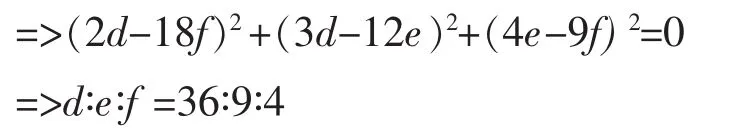
这种解法计算量较大。

为了强化训练柯西不等式的应用，老师又出了几道作业题，来提高学生对该不等式的认识。

作业 3. 对于一切实数 x，y，z 满足（x2＋y2＋z2）2≤n（x4＋y4＋z4）的最小整数 n 是 （）

(A)2 (B)3 (C)4 (D)6

解：（x2＋y2＋z2）2≤（12＋12＋12）（x4＋y4＋z4）

＝3（x4＋y4＋z4）

当x2=y2=z2时，上式等号成立。所以n的最小值为3。

作业 4. 已知 a，b，c≥0 且 a＋b＋c＝1，

作业 5.已知 a，b，c∈R+，求证

上式两边同除以（a+b+c）有：

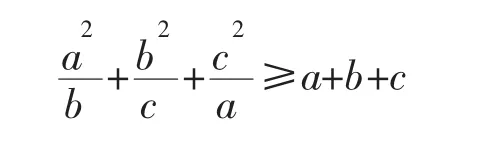
作业 7. 已知 x＞0，y＞0 且 x＋y＝1，求证：

证：设 x＝cos2θ，y＝sin2θ

作业 8. 已知 sin2A＋sin2B＋sin2C＝1，