一种圆锥形变幅杆弯曲振动固有频率的计算方法

严日明， 刘德福,2， 陈　涛， 佘亦曦

(1.中南大学 机电工程学院，长沙　410083; 2. 高性能复杂制造国家重点实验室，长沙　410083)



一种圆锥形变幅杆弯曲振动固有频率的计算方法

严日明1， 刘德福1,2， 陈涛1， 佘亦曦1

(1.中南大学 机电工程学院，长沙410083; 2. 高性能复杂制造国家重点实验室，长沙410083)

摘要：提出了一种圆锥形变幅杆弯曲振动固有频率的计算方法;先忽略剪切变形和惯性矩作用，基于Euler-Bernoulli杆理论求解出固有频率初值，再计入二者的作用进行弯曲振动固有频率的修正。应用有限元分析法和模态实验测试对该方法进行验证，理论结果与实验结果吻合，误差<5%。基于该方法编写程序，实现了弯曲振动变幅杆结构的主动设计。

关键词：圆锥形变幅杆；超声弯曲振动；固有频率

近年来，超声振动在脆硬材料精密加工中的应用越来越广泛。由于弯曲振动模式具有更好的声匹配性，在超声加工装置中采用弯曲振动模式，或者弯曲振动和纵向、扭转复合振动模式，加工效率高且质量更好，正成为超声加工领域的重要发展趋势之一[1]。清华大学对蓝宝石衬底进行了超声弯曲振动辅助化学机械抛光(UFV-CMP)加工，提高了表面粗糙度、平面度和材料去除率[2]。Norikazu SUZUKI等[3]采用双向弯曲振动实现椭圆振动对脆硬性材料进行了微细加工，得到了1.9 μm深的无脆性断裂的微小槽，且提高了表面质量和临界切削深度。Xun Li等[4]采用纵弯复合椭圆振动系统对SI235进行了切削加工，大幅降低了切削力、轴向力和表面粗糙度。诸多研究表明，带弯曲振动模式的超声装置对于超声加工至关重要。超声变幅杆作为超声振动装置的核心部件，其纵向和扭转振动研究目前已趋于成熟，而弯曲振动由于其振动规律的复杂性，使得该技术不够完善和系统，导致其实际应用受到限制[5]。

超声变幅杆是功率超声设备中的关键部件，主要实现能量的传输和聚能[6]，按其结构一般分为阶梯形杆和连续变截面杆。对于大多数具有较高的工作稳定性和较大的抗弯刚度要求的场合，连续变截面杆应用更普遍。在放大系数要求不高时，又以圆锥形变幅杆最为适用，其弯曲振动固有频率的计算对于其在超声加工中的应用至关重要。对于阶梯形杆的弯曲振动，通过求解简单的常系数微分方程可求得其固有频率的精确值[7]，并且已研制出阶梯形变幅杆纵弯复合超声振动系统[8]。对于连续变截面杆的弯曲振动固有频率计算方法的研究，目前只见到半精密解法[9]和矩阵解法[10]，其原理都是基于分段思想把一段变截面杆近似看成若干段等截面杆的组合，利用等截面杆的固有频率计算方法通过矩阵传递求出整段杆的固有频率。此法适用于各种类型的变截面杆，可以得到一定精确度的固有频率近似值，但计算过程很复杂，计算量庞大。在超声振动系统的设计过程中，也往往需要根据特定边界条件和给定的振动频率设计变幅杆的结构尺寸，即主动设计。目前有限元分析法在给定结构尺寸的模态分析方面较精确，但在设计给定弯曲振动频率的杆件尺寸时一般只能通过试凑法。作为一种被动设计过程，该方法显得过程繁琐且工作量庞大。

以Euler-Bernoulli杆理论为基础，通过研究连续变截面杆的弯曲振动方程，并以圆锥形超声变幅杆为例，直接求解四阶变系数线性微分方程，得到杆的弯曲振动方程通解，从而得到不同边界条件下的圆锥形变幅杆弯曲振动固有频率。通过对比分析Euler-Bernoulli杆理论和Timoshenko杆理论，对所求的弯曲振动固有频率初值提出了修正公式，可用于不同材料、不同尺寸、不同阶次下的弯曲振动固有频率求解。在得到精确度较高的弯曲振动固有频率解的同时，为弯曲振动、纵弯复合、扭弯复合振动圆锥形变幅杆的设计提供了理论基础，拓宽了圆锥形变幅杆在超声加工中的应用。

1圆锥形变幅杆弯曲振动固有频率

1.1基于Euler-Bernoulli杆理论的变截面杆弯曲振动固有频率

基于Euler-Bernoulli杆理论，已知长为l，截面面积为A(x)的任意杆，横截面形心的连线为x轴，推导变截面杆在主惯性轴方向上弯曲振动的波动方程。

设杆在xoy平面上的挠度、转角、弯矩及剪力分别为Y(x,t)、θ(x,t)、M(x,t)和Q(x,t)，其正方向(见图1)。假设振动发生在的弯曲杆的一个主平面上，其横截面尺寸与杆的长度比较小，上述物理量满足如下关系：

(1)

式中：E为材料弹性模量；I(x)为杆任意横截面对中性轴的惯性矩。

根据达朗贝尔原理：

(2)

式中：ρ为材料密度；A(x)为杆任意横截面的截面面积。

图1　任意变截面杆弯曲示意图Fig.1 Bend of bar with vari-cross-section

联立式(1)和式(2)，得到任意变截面杆的弯曲波动方程为：

(3)

将式(3)左边括号内的项对x进行二次微分计算，则方程展开得到：

(4)

在简谐振动中，设任一点x处的弯曲振动为

Y(x,t)=y(x)ejwt

(5)

式中：y(x)为杆弯曲振动的振型函数；ω=2πf，为杆弯曲振动角频率；f为杆的弯曲振动频率。将(5)式代入式(4)可得基于Euler-Bernoulli杆理论的通用变截面杆弯曲波动方程：

(6)

针对不同横截面形状的变截面杆，只要将其惯性矩I(x)、截面面积A(x)代入式(6)即可得到该变截面杆的弯曲波动方程。求解该方程，并利用特定的边界条件，可求得该杆基于Euler-Bernoulli杆理论的各阶弯曲振动固有频率fEi。

1.2圆锥形杆弯曲振动方程及其求解

在超声领域，圆锥形变幅杆由于弯曲劲度较大，工作稳定性高，且机械加工成本低，在不要求特别大的放大系数的条件下，得到了非常广泛的应用[11]。故以圆锥形杆为例，求解其弯曲振动方程，并得到其在不同边界条件下的弯曲振动固有频率，从而为弯曲振动圆锥形变幅杆的设计奠定基础。

圆锥形变幅杆结构见图2，大端直径为D1，小端直径为D2，杆长为l，在任意位置x处，其直径D(x)、横截面面积A(x)、杆任意横截面对中性轴的惯性矩I(x)满足式(7)。

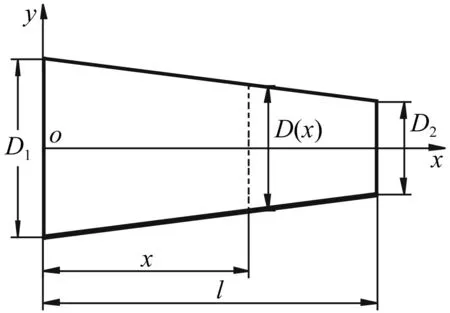
图2　圆锥形变幅杆结构简图Fig.2 Conical horn

(7)

将式(7)代入式(6)，化简得到：

(8)

式中：α=(D1-D2)/l，则D(x)=D1-αx，从而有：

(9)

将式(9)代入式(8)得到圆锥形杆的弯曲振动的波动方程：

(10)

令λ2=16ρω2/Eα4=64π2ρf2/Eα4，则式(10)有如下形式通解[12]：

(11)

将D(x)=D1-αx代入式(11)式即可得到归一化的圆锥形杆的弯曲振动振型函数。

式中：J2(x)、Y2(x)为二阶第一类贝塞尔函数、二阶第二类贝塞尔函数。其定义为[13]：

(12)

为了便于推导频率方程，将式(11)等效变形为：

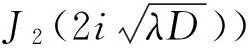
(13)

分别令：

得到：

(14)

从而得到：

(15)

式中：根据两类贝塞尔函数求导的性质[13]：

(16)

从而得到：

(1) 一阶导数：

(17)

(2) 二阶导数：

(18)

(3) 三阶导数：

在不同的边界条件下，位移函数y有不同的物理特性。以通解为基础，通过分析这些特性，可以建立对应边界条件下的物理特征方程组，从而得到频率方程，即可求解出杆件的固有频率。

1.3圆锥形变幅杆在不同边界条件下的弯曲振动固有频率

(1) 边界自由时，弯矩和剪力分别为0，即：

(20)

可解得在自由边界条件下，有：

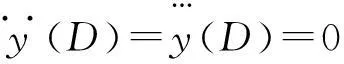
(21)

(2) 边界固定时，其挠度和转角分别为0，即：

(22)

可解得在固定边界条件下，有：

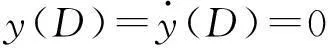
(23)

(3) 边界铰支时，其挠度和弯矩分别为0，即：

(24)

可解得在铰支边界条件下，有：

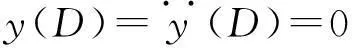
(25)

由以上推导可知，在变幅杆两端的不同边界条件下，可以推导出频率方程。在圆锥形变幅杆两端自由边界条件下，有：

(26)

结合弯曲振动振型函数式(11)和边界条件式(26)，得到：

(27)

从而转为求解系数矩阵行列式为0的方程：

(28)

可解得弯曲振动固有频率f与圆锥形变截面杆尺寸l、D1、D2之间的关系，式(28)即为在两端自由边界条件下，圆锥形变幅杆弯曲振动频率方程。

同理，可以推导其他边界条件下的频率方程(见表1)。此外，还可根据该过程推导出其他特殊的边界条件和频率方程。

解上述频率方程，分别按照解的大小顺序求得各圆锥形杆对应边界条件下的各阶弯曲振动固有频率初值fEi。

1.4圆锥形变幅杆弯曲振动固有频率的修正模型

由于Euler-Bernoulli杆理论没有考虑剪切变形和惯性矩的作用，计算结果对于细长杆适用，但是对于长径较小的杆的计算误差偏大，此时用计入剪切变形和惯性矩作用的Timoshenko杆理论计算更加精确。

本节对Euler-Bernoulli杆理论和Timoshenko杆理论的振动微分方程进行对比探讨，在等截面杆理论基础上计入杆件形状、剪切变形和惯性矩作用对Euler-Bernoulli杆理论计算所得弯曲振动固有频率初值fEi进行修正。

与Euler-Bernoulli杆理论相比，Timoshenko杆理论仍然采用平剖面假设，但放松了剖面始终垂直于杆挠度曲线的假设，因此剖面转角不再与挠度曲线的一阶导数相等，即杆可以发生剪切变形。该理论将挠度Y(x,t)和转角θ(x,t)视为两个独立的变量，分别建立振动微分方程[14]：

(29)

式中：G=E/2(1+ν)，为杆件的剪切模量；k为不同截面下的剪切系数。对于圆形横截面，k=6(1+ν)/(7+ν)，ν为泊松比。

同理，基于简谐振动，令：

Y(x,t)=y(x)ejwt,θ(x,t)=φ(x)ejwt

(30)

将式(30)代入式(29)可得基于Timoshenko杆理论的通用变截面杆弯曲波动方程：

(31)

式中：ω为杆弯曲振动角频率，惯性矩I(x)、截面面积A(x)仍然为沿x方向连续变化的函数，其关于x微分展开和求解非常复杂，目前还不能得到二阶二元微分方程式(31)的解析解，所以很难求解基于Timoshenko杆理论的变截面杆的弯曲振动固有频率。对于等截面杆，Euler-Bernoulli杆理论有：

(32)

根据式(31)，在均匀等截面杆条件下消去φ，则对Timoshenko杆理论有：

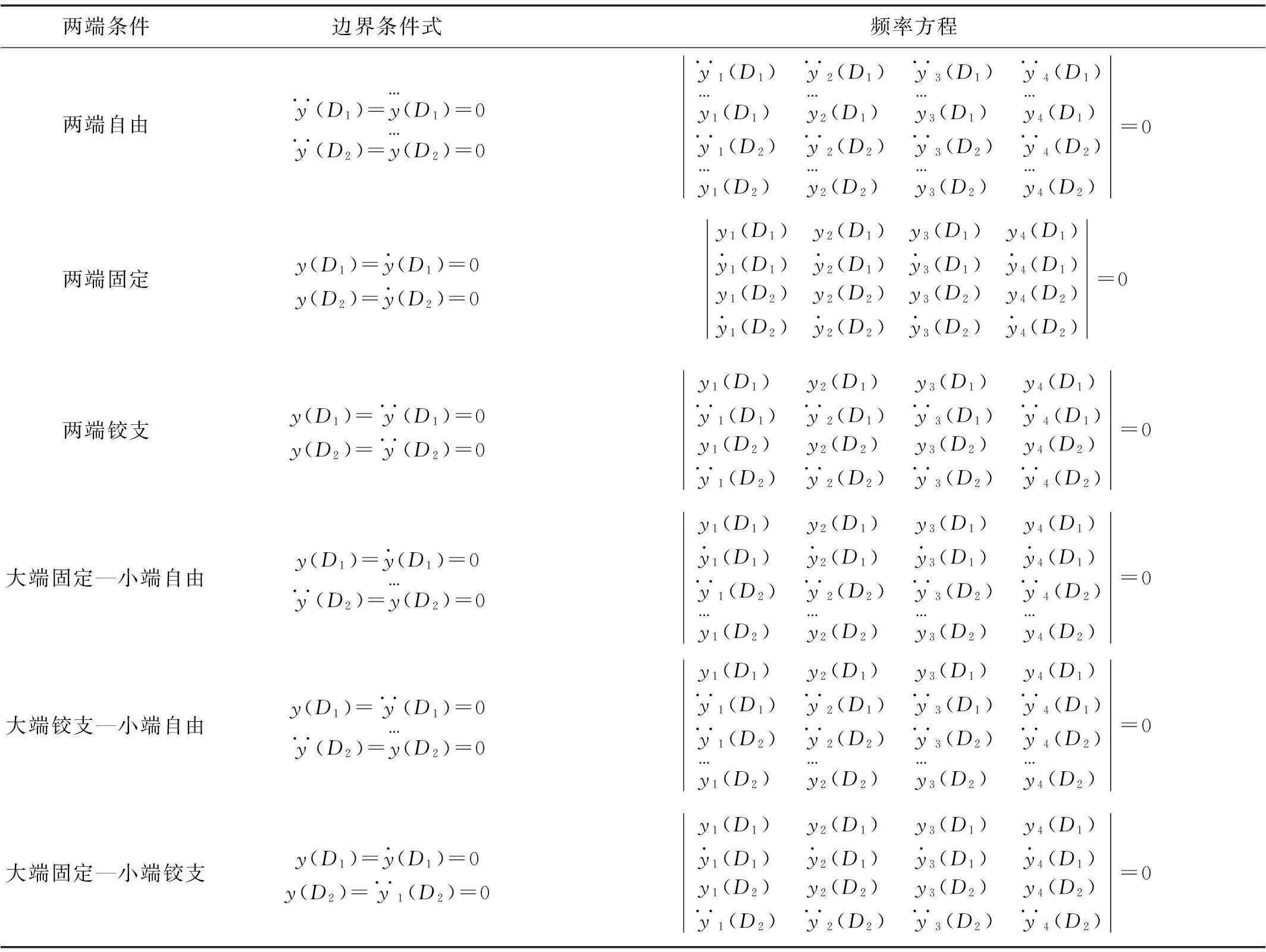
表1　各边界条件下圆锥形变幅杆弯曲振动频率方程

(33)

式中：超声变幅杆一般基于自由振动状态进行设计，在计算频率时可对等截面杆振型函数取近似：

(34)

对振动频率计算结果影响不大[15]。对式(34)求二阶导数可得：

(35)

对式(33) 忽略微小量系数的第四项，结合式(35)，可得到：

(36)

将式(32)代入式(36)可得：

(37)

化简式(37)，并结合式(7)中I和A的关系得到：

(38)

为了基于等截面杆对圆锥形杆进行修正，提出形状系数：

(39)

式中：β越大，杆越粗短，反之越细长。以此将(见图2所示圆锥形杆近似成计入形状系数的等截面杆，并代入式(38)得到计入形状系数、剪切变形和惯性矩的修正公式为：

(40)

式中：fFi为修正计算所得i阶弯曲振动固有频率，单位为Hz；fEi为上节所述基于Euler-Bernoulli杆理论计算所得i阶弯曲振动固有频率初值，单位为Hz；i为弯曲振动阶次。

1.5实验验证

为了验证圆锥形杆弯曲振动固有频率计算方法，加工了三根不同尺寸的圆锥形杆，材料为6061铝合金，其弹性模量E=69 GPa，泊松比ν=0.33，材料密度ρ=2 700 kg/m3。变幅杆尺寸见表2。加工所得实验工件见图3。

表2　圆锥形变幅杆尺寸

图3　圆锥形变幅杆Fig.3 Conical horns

为了最大程度减少外界作用对杆件的干扰，且超声变幅杆一般基于自由振动状态进行设计，故对各杆分别进行自由边界条件下的弯曲振动固有频率的计算及验证。

基于表2所示圆锥形变幅杆的尺寸参数和弯曲振动频率方程， 应用Matlab数值解法求解得到前4阶弯

振频率初值fE，基于式(40)算得弯曲振动固有频率fF。基于有限元模态分析法，得到弯曲振动各阶固有频率有限元计算结果。最后加工圆锥形杆，采用动态信号测试分析系统，通过敲击法进行模态实验测量，测试原理见图4。

经敲击法模态实验测试得到50 kHz内锥形杆的固有频率，通过分析模态测量的振形结果可得到固有频率中弯曲振动频率值。三根杆弯曲振动固有频率的计算结果、有限元分析结果和模态实验测试结果见表3。

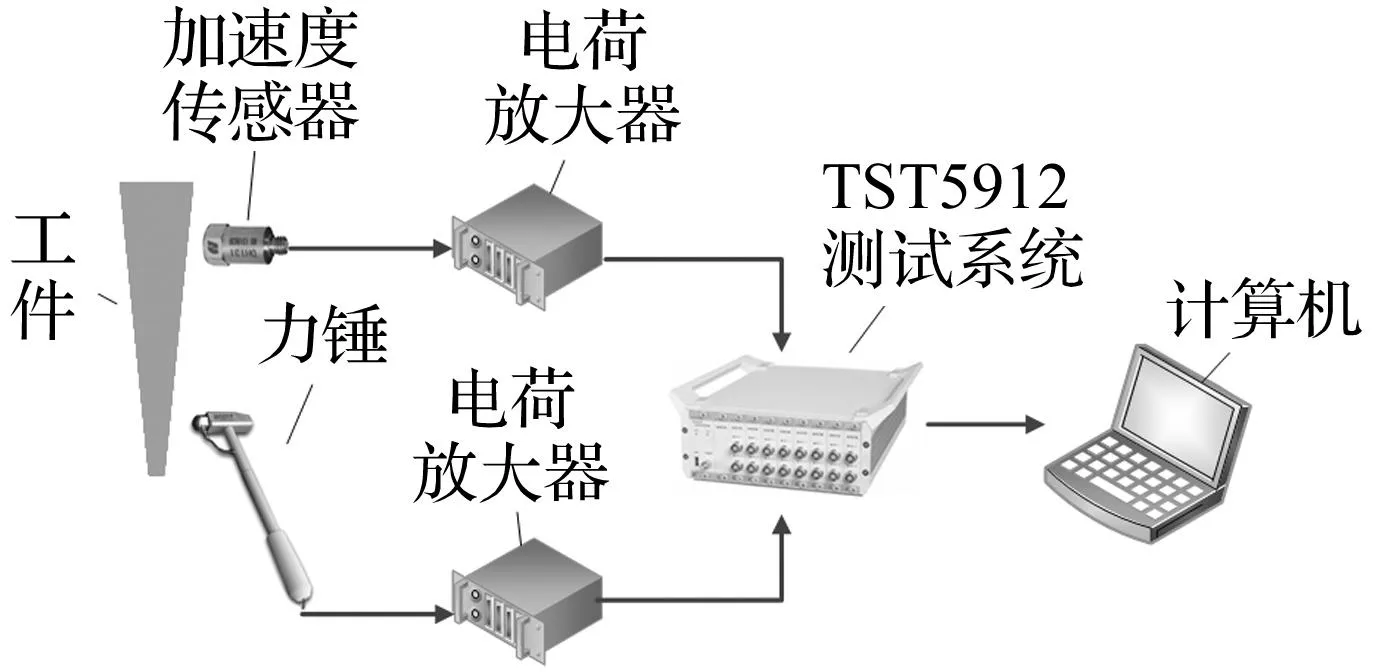
图4　敲击法测量变幅杆的弯曲振动固有频率Fig.4 Measurement of flexural vibration frequency of horn using striking method

表3的数据表明本文提出的变截面杆弯曲振动固有频率计算方法的计算结果与有限元分析、弯曲振动模态测试结果均吻合较好。

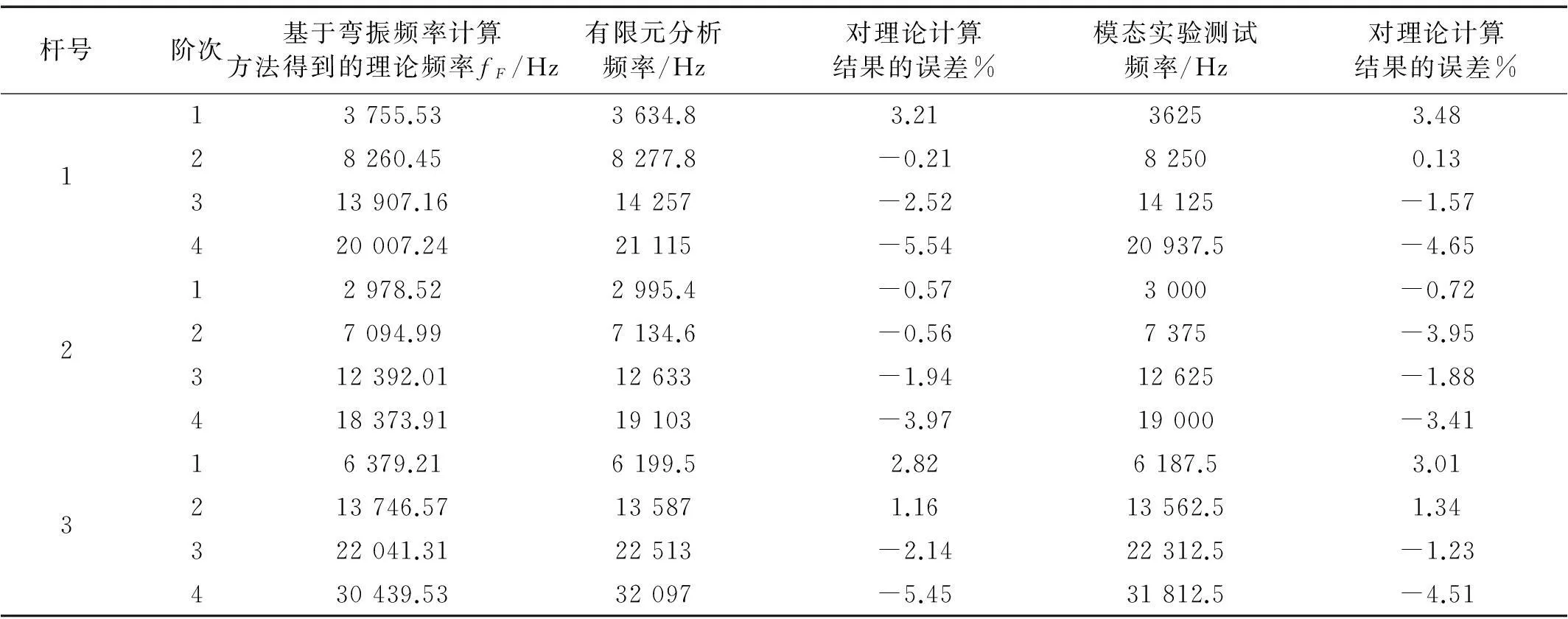
表3　自由状态下各杆前4阶弯曲振动固有频率的理论计算与验证

2给定弯曲振动频率的圆锥形变幅杆的设计

基于本文提出的圆锥形变幅杆弯曲振动固有频率计算方法，介绍圆锥形变幅杆在超声弯曲振动应用中的设计过程。

为了研究圆锥形变幅杆固有特性，减少其他外在条件的影响，结合弯曲振动变幅杆设计时的一般边界条件，选择两端自由的边界条件进行设计。基于本文所述方法，在超声换能器的设计过程中，可以根据任一端直径和形状系数设计另一端直径。在此以给定圆锥形变幅杆小端尺寸D2和形状系数β的设计为例，探讨基于给定的弯曲振动频率要求进行超声变幅杆设计的思路。

本文要求设计出在20 kHz 、25 kHz 和30 kHz下分别实现1阶、2阶、3阶的自由弯曲振动的圆锥形变幅杆。其设计过程与弯曲振动固有频率计算过程相反：通过修正式(40)求得各阶弯曲振动频率fFi对应的频率初值fEi，结合对应边界条件下的频率方程和形状系数β，算得大端直径D1和杆长l。

表3证明了有限元模态分析结果与实际测试结果十分吻合，故可用有限元模态分析结果近似代替实验结果来对变幅杆杆设计结果进行验证，结果见表4。由表4可知，本文提出的圆锥形变幅杆弯曲振动固有频率计算方法非常可靠。

表4　弯曲振动圆锥形变幅杆设计结果及有限元验证

3结论

本文基于Euler-Bernoulli杆理论建立了圆锥形变幅杆弯曲振动固有频率计算方法。可得到如下主要结论：

(1) 基于Euler-Bernoulli杆理论，推导了任意变截面杆的弯曲振动方程，并以圆锥形杆为例，得到了圆形截面的变截面杆的弯曲振动方程，并求得了四阶微分方程的通解，分别建立了不同边界条件下弯曲振动频率方程。

(2) 在Euler-Bernoulli杆理论基础上，计入形状系数、剪切变形和惯性矩作用，得到了圆锥形变幅杆弯曲振动固有频率的修正公式，并在自由边界条件下分别进行了有限元模态分析验证和模态实验测试验证。本文提出的圆锥形变幅杆弯曲振动固有频率计算方法所得计算结果与模态实验测试结果和有限元分析结果的误差均<5%。

(3) 基于本文提出的圆锥形变幅杆弯曲振动固有频率计算方法，在给定弯曲振动频率的条件下设计了三种锥形变幅杆。有限元模态分析结果表明，圆锥形变幅杆弯曲振动固有频率与设计要求偏差很小，实现了基于给定弯曲振动频率和阶数的弯曲振动圆锥形变幅杆的主动设计。

参 考 文 献

[ 1 ] 张雄,焦锋. 超声加工技术的应用及其发展趋势[J]. 工具技术,2012(1):3-8.

ZHANG Xiong, JIAO Feng.Applications and development trends of ultrasonic machining technology[J]. Tool Technology,2012(1):3-8.

[ 2 ] Xu W, Lu X, Pan G, et al. Ultrasonic flexural vibration assisted chemical mechanical polishing for sapphire substrate[J]. Applied Surface Science, 2010, 256(12): 3936-3940.

[ 3 ] Suzuki N, Masuda S, Haritani M, et al. Ultraprecision micromachining of brittle materials by applying ultrasonic elliptical vibration cutting[C]//Micro-Nanomechatronics and Human Science, 2004 and The Fourth Symposium Micro-Nanomechatronics for Information-Based Society, 2004. Proceedings of the 2004 International Symposium on. IEEE, 2004: 133-138.

[ 4 ] Li X, Zhang D. Ultrasonic elliptical vibration transducer driven by single actuator and its application in precision cutting[J]. Journal of Materials Processing Technology, 2006, 180(1): 91-95.

[ 5 ] 林书玉. 超声换能器的原理与设计[M]. 北京：科学出版社, 2004.

[ 6 ] 潘巧生,刘永斌,贺良国,等. 一种大振幅超声变幅杆设计[J]. 振动与冲击,2014,33(9):1-5.

PAN Qiao-sheng, LIU Yong-bin, HE Liang-guo, et al.Design of an ultrasonic horn with high amplitude of longitudinal vibration[J]. Journal of Vibration And Shock, 2014,33(9):1-5.

[ 7 ] Timoshenko S. Vibration problems in engineering[M].2nd.D. Van Nostrand Company, Inc. New York, 1937.

[ 8 ] Watanabe Y, Tsuda Y, Mori E. A longitudinal-flexural complex-mode ultrasonic high-power transducer system with one-dimensional construction[J]. Japanese Journal of Applied Physics, 1993, 32(5S): 2430.

[ 9 ] 崔灿,李映辉. 变截面铁木辛柯梁振动特性快速计算方法[J]. 动力学与控制学报,2012,(3):258-262.

CUI Can, LI Yin-hui, A solution for vibration characterist of timoshenko beam with variable cross-section[J].Journal of Vibration and Shock,2012,(3):258-262.

[10] Zhou Guang-ping, Li Ming-xuan, A study on ultrasonic solid horns for flexural mode[J]. Journal of Acoustical Society of American, 2000,107(3):1358-1362.

[11] 曹凤国.超声加工[M]. 北京：化学工业出版社, 2013.

[12] Kamke E. Handbook of ordinary differential equations[M]. Chelsea Publ, 1976.

[13] 奚定平.贝塞尔函数[M]. 北京：高等教育出版社,1998.

[14] 邢誉峰,李敏. 计算固体力学原理与方法[M]. 北京：北京航空航天大学出版社,2011.

[15] 方同, 薛璞. 振动理论及应用[M].西安：西北工业大学出版社,1998.

A calculation method for flexural vibration frequencies of a conical horn

YANRi-ming1,LIUDe-fu1,2,CHENTao1,SHEYi-xi1(1. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)

Abstract:A method for calculation of flexural vibration frequencies of a conical horn was presented. Firstly, its initial flexural frequency values ignoring effects of shear deformation and moment of inertia were solved based on Euler-Bernoulli beam theory, and then they were corrected considering both of the effects. The FEM and the modal test showed that the results obtained from calculation agree well with those of tests, the error is within 5%. The active design of a flexural vibration horn was realized with the code based on the proposed method.

Key words:conical horn; ultrasonic flexural vibration; natural frequency

中图分类号:TH122；TH113.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.030

通信作者刘德福 男，教授，博士生导师，1971年生

收稿日期：2015-03-05修改稿收到日期：2015-04-15

基金项目：国家自然科学基金项目(51275534)；湖南省自然科学基金项目(2015JJ2153)

第一作者 严日明 男，硕士，1992年生