新型双足模型下结构动力响应分析

王益鹤， 杨　娜

(北京交通大学 土木建筑工程学院，北京　100044)



新型双足模型下结构动力响应分析

王益鹤， 杨娜

(北京交通大学 土木建筑工程学院，北京100044)

摘要：基于考虑人体动力特性的新型双足模型，采用Lagrange方程建立了步行过程中人与结构相互作用系统运动方程。研究了人与结构各自的动力响应及其之间相互作用，并通过对比说明了新型双足模型反映的人体动力特性对结构振动的影响。结果表明：人与结构相互作用增大结构动力响应；行人经过结构各阶模态振型波峰时，结构各阶模态频率和阻尼比分别达到最小值和最大值。

关键词：振动；双足模型；人与结构相互作用；动力特性

在土木工程领域，人行激励下的结构振动问题尤其是人与结构相互作用问题，越来越受到人们的关注[1-2]。如设计不当，结构会在人群行走、跑步等运动下出现较大的振动响应，导致其舒适性和安全性下降。

众多学者建立了各种数学模型描述人行激励。其中最常见的是用傅里叶级数表达为静载荷与几个简谐动载荷之和的确定性模型[3-4]。然而这种方式仅仅把人看作移动载荷，忽略了人作为独立的动力体系这一特性，未考虑人与结构相互作用，预测具有轻质、低频等特点的柔性结构振动时，不仅结果有所偏差，且无法研究人体对结构振动的反应和舒适情况。

考虑人体动力特性的生物模型开始应用于人与结构系统。人体被简化为不同自由度的刚度、质量和阻尼体系(Spring Mass Damper,SMD)[5-7]。进一步研究表明[8-9]，双自由度(2 Degree of Freedom,2-DOF)的SMD模型较之单自由度(Single Degree of Freedom,SDOF)SMD模型，能更好的描述人体振动特性。而自由度更高的模型则用来研究振动在人体不同部位的精细传递过程，不适用于人与结构相互作用[10]。Kim等[11]也采用ISO 5982[12]的2-DOF人体模型分析人行桥的竖向振动问题。然而SMD模型仅能表示人体的竖向运动，无法反映人体步态尤其是行人步行中双足支撑阶段时的特性。故其不能很好的理解结构振动对人体动载荷的改变。Geyer等[13]提出用双足模型模拟人体的步行运动，后来一些研究人员[14-15]也对双足模型进行了分析，但均将人身体表示为质心，忽略了2-DOF人体模型所精确描述的人体动力特性，不能全面考虑人体对结构振动的影响。

本文综合考虑ISO 5982的2-DOF模型描述的人体动力特性及双足模型的双足步行特点，建立了新型双足步行模型。分别对人与结构相互作用系统中的人和结构进行了动力分析，并研究了新型双足步行模型中人体动力特性对结构动力响应的影响。

1人与结构相互作用系统运动方程

新型双足模型采用ISO 5982模型表示身体，人体质量等效为质量m1和m2，身体刚度为k1，阻尼为c1，长度为lb；腿部由两个无质量的等长弹簧和阻尼表示的体系构成，其弹簧刚度为k1eg，阻尼为cleg，长度为l0(见图1)。

图1　新型双足模型步行原理图Fig.1 Schematic of the new bipedal model

采用Lagrange方程建立人与结构系统运动方程，人行桥由Euler-Bernoulli简支梁表示。系统模型(见图2)。在双足支撑阶段，人与结构系统的动能和势能分别表示为：

图2　人与结构相互作用系统模型Fig.2 Modal of human-structure interaction system

(1)

(2)

式中：z1、z2和u分别为人体m1和m2的垂直位移和水平位移;Ll和Lt分别为支撑腿和随动腿弹簧长度;y为梁的垂直位移，y″(x,t)为曲率;m为单位长度梁质量;E为弹性模量;g为重力加速度。

梁的垂直位移由振型叠加法可表示为：

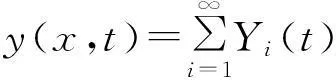
(3)

式中：{φi(x),i=1,2,…,n}为梁的振型;{Yi(t),i=1,2,…,n}为广义坐标。

人与结构系统虚功的变分δW可表示为：

F1δz1+F2δz2+F3δu

(4)

式中：cl、ct和cs分别为支撑腿、随动腿和结构的阻尼；vl和vt为两腿的轴向速度；δ(ΔLl)和δ(ΔLt) 为两腿的虚变形;{δYi,i=1,2,…,n}为梁的虚位移；δy″为梁曲率的变分；Q1,Q2,…，Qn,F1,F2,F3为对应广义坐标{Y1,Y2,…，Yn,z1,z2,u}的广义力。

支撑腿长度和随动腿长度分别由其相对位置，可表示为：

(5)

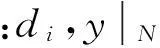
支撑腿和随动腿的轴向速度，可由m2与前后落脚点位置的相对竖向速度和及其水平速度合成得出，

(6)

式中：θl,θt分别为支撑腿和随动腿与地面的夹角。

同理，支撑腿和随动腿的位移变分，也可根据相对位移关系合成得出，

将式(3)和式(5)分别代入式(1)和式(2)，可得：

(8)

(9)

将式(3)、式(6)和式(7)分别代入到式(4)中，虚功变分δW可表示为，

(10)

对比式 (4)和式 (10)，广义力表示为：

(11)

系统Lagrange方程可以表示为：

(12)

把动能、势能和广义力的表达式代入Lagrange方程，人与结构系统的运动方程表示为：

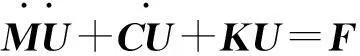
(13)

(14a)

(14b)

(14c)

(14d)

式中:

ci,i=2ξiwiMi+clsin2θlφi,i(N)+ctsin2θtφi,i(N-1),(i=1,2,…,n)

ci,j=clsin2θlφi,j(N)+ctsin2θtφi,j(N-1),(i≠j≤n)

ci,n+2=-clsin2θlφi(N)-ctsin2θtφi(N-1),(i=1,2,…,n)

ci,n+3=clsinθlcosθlφi(N)-ctsinθtcosθtφi(N-1),(i=1,2,…,n)

cn+2,i=-clsin2θlφi(N)-ctsin2θtφi(N-1),(i=1,2,…,n)

cn+3,i=clsinθlcosθlφi(N)-ctsinθtcosθtφi(N-1),(i=1,2,…,n)

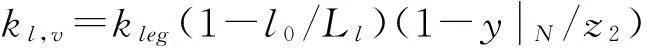
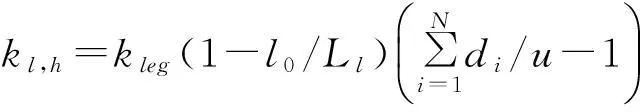
φi,j(N)=φi(N)φj(N),φi(N)=

(15)

上述分析过程针对双足支撑阶段。而单足支撑阶段时，随动腿不与地面接触，将所有与随动腿相关的量设置为零即可。

由于双足模型中存在阻尼耗能，故需提供外在机制进行控制。否则系统运动方程无法保持平衡，双足模型经若干步后将失去稳定[13-15]。本文采用水平外力做功的方式维持系统能量恒定。水平控制力表示为如下形式：

(16)

式中：E0为人体初始能量;E(t)为时刻t时人体能量;Δu(t)为时刻t时人体水平位移增量。

人体总能量E(t)由动能、弹性势能和重力势能构成，可以表示为：

(17)

则式(14)中载荷向量变为：

F(t)=[0,0,0,…,k1lb-m1g,

(18)

由于系统中阻尼矩阵和刚度矩阵时变且含有未知量，故需用迭代的方法确定位移增量及速度增量。本文选取Newton-Raphson非线性方法进行迭代求解。

2人与结构相互作用分析

为了研究新型双足模型下人与结构的相互作用，本文对上述推导过程进行Matlab编程，详细分析整个系统的响应及动力特性。并将基于新型双足模型的计算结果与基于时域力模型的计算结果进行比较。

2.1人与结构系统振动分析

对于双足模型，腿刚度kleg、冲击角θ0和步行初始速度v，是影响人体运动的关键参数。Geyer[13]首先给出腿刚度kleg和冲击角θ0的参数区域图，并得出双足模型步行初始速度v的适用范围为0.8～1.6 m·s-1。Whittington[14]列出了腿刚度kleg<50 kN·m-1，冲击角θ0在50°～80°内的参数区域图。Kim[16]将腿刚度kleg取值为14～28 kN·m-1，且认为阻尼比ξ在3%～8%范围内即可描述人体步行。

新型双足模型选取以下人体特性：身体部位参考ISO 5982模型[12]，人体质量mh=75 kg(其中m1=62 kg,m2=13 kg)，身体刚度k1=62 kN·m-1，身体阻尼c1=14.6 kN·s·m-1，身体长度取lb=0.4 m；腿部参数根据已有双足模型[13-16]，取腿刚度kleg=20 kN·m-1，阻尼比ξ=8%，腿长取为l0=1 m。步行初始速度为1.0 m/s，在运动过程中假定冲击角θ0=69°为常数。

为阐述人与结构相互作用，假定两个简支人行桥。①算例一：刚度较大人行桥，11.0 m×1.25 m×0.35 m。材料特性为：单位长度质量m=1.364×103kg·m-1，刚度EI=1.64×108N·m2，模态阻尼比为ξ=0.3%。空载桥的前两阶频率为：f1=4.50 Hz，f2=18.01 Hz。②算例二：柔度较大人行桥，9.0 m×0.8 m×0.1 2m。材料特性为：密度为2 400 kg·m-3，弹性模量E为3×1010N·m-2，模态阻尼比为ξ=0.3%。空载桥的前两阶频率为：f1=2.375 Hz ，f2=9.50 Hz。

众多研究者根据人体表观质量幅频特性研究人体模型[17]。图3所示为新型双足模型的人体表观质量幅频特性曲线。由图3可知，新型双足模型的人体表观质量幅频特性曲线与ISO 5982模型相近。由于ISO5982模型是由人体振动响应幅频特性所得出，故新型双足模型在模拟人体步行运动时，也可反映人体自身动力特性。

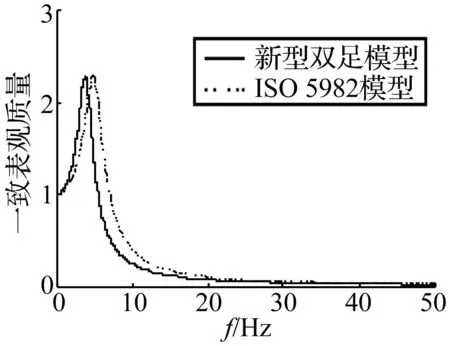
图3　人体表观质量幅频特性Fig.3 Normalised apparent masses response functions

图4所示为根据选取参数所得的行人单步步行载荷。新型双足模型能够捕捉人体重心变化产生的加速度及模拟两腿交替行进，从而可得步行载荷的双峰值特性。模拟得到的步行载荷特征与众多的研究者试验结果一致，可知新型双足模型可较好的模拟人体的步行特性。

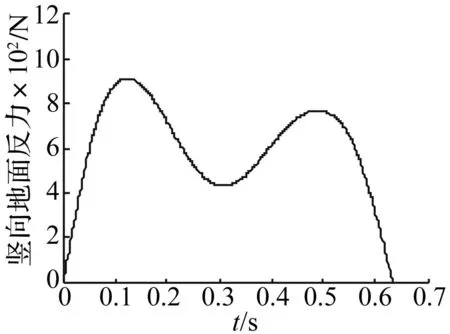
图4　单步竖向地面反力Fig.4 Vertical ground reaction force with one foot

2.1.1算例一

首先对刚度较大的人行桥进行分析。图5和图6为行人经过刚度较大人行桥时跨中的位移和加速度时程。虚线为采用图4中地面反力时程得到的人行桥跨中动力响应。由图4可知，两种方式所得结果差异较小。即结构刚度较大，振动响应较小，人与结构的相互作用较小。

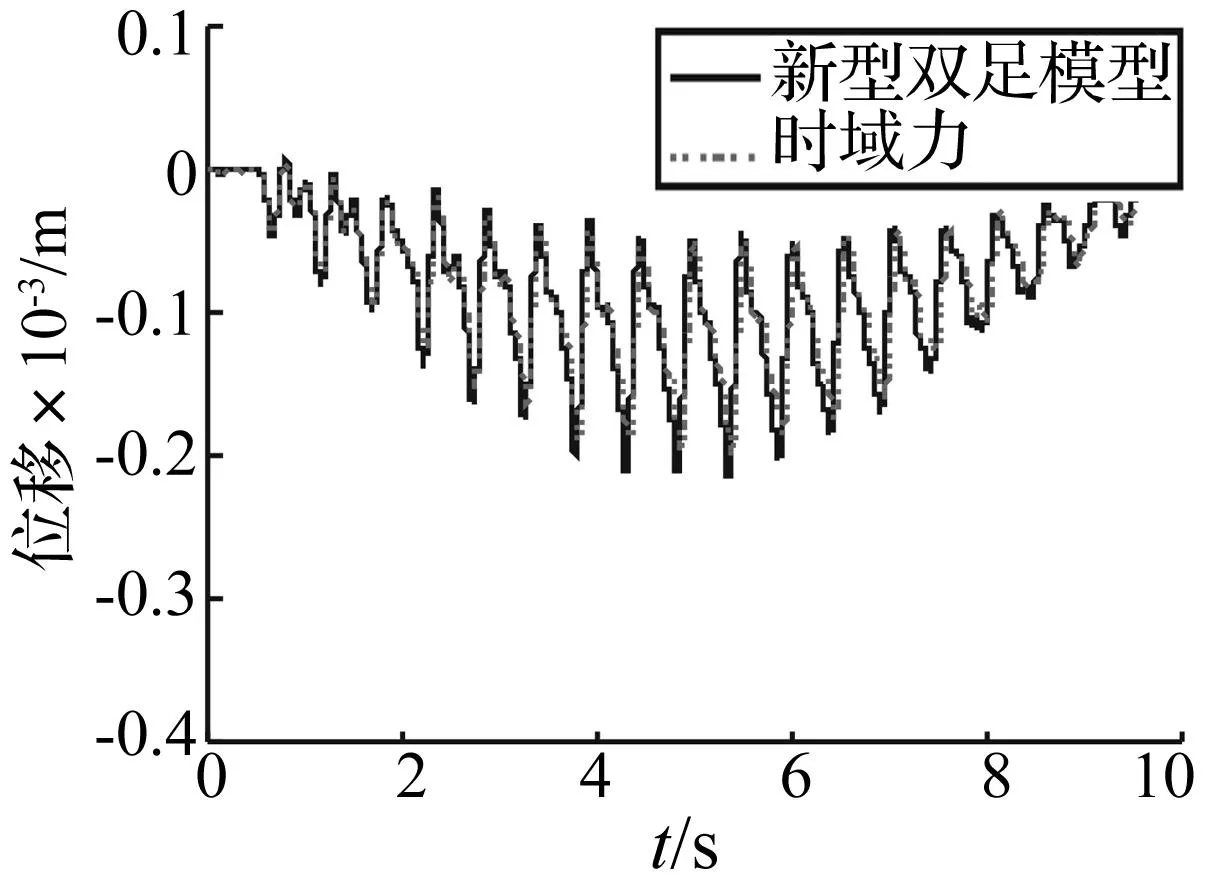
图5　人行桥的跨中位移Fig.5 Displacement at midspan of bridge

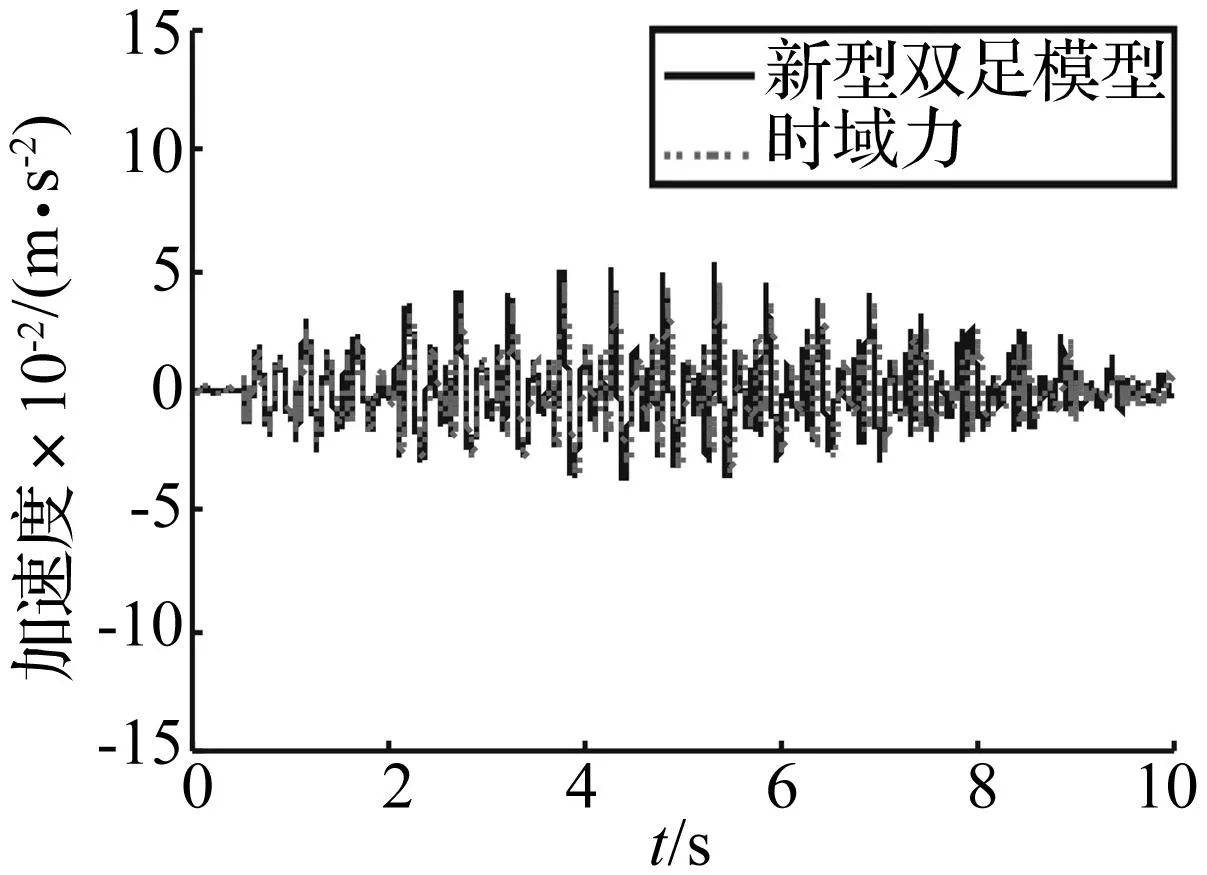
图6　人行桥的跨中加速度Fig.6 Acceleration at midspan of bridge

图7为行人步行通过结构时的竖向地面反力。由图7可知，人与结构的相互作用较小，竖向地面反力时程平稳，结构振动对步行载荷的影响较小。

图7　步行中产生的竖向地面反力Fig.7 Vertical ground reaction force in walking

由以上分析可知，结构刚度较大时，人与结构的相互作用较小。

2.1.2算例二

为分析人与结构相互作用，以下对柔度较大人行桥进行详细分析。

图8和图9为行人经过柔度较大人行桥时跨中的位移和加速度响应时程。虚线为采用图4中地面反力时程得到的人行桥跨中动力响应。由图可知，两种方式所得计算结果差异明显。新型双足模型所得最大位移值和最大加速度值分别比时域力模型大24%和37%。差异表明人与结构相互作用较大。即结构较大的振动引起新型双足模型中腿部弹簧较大的变形，而腿部离开接触面时弹簧中储藏的弹性势能得以释放，使得行人又明显影响结构响应，从而人与结构相互作用显著。

图8　人行桥的跨中位移Fig.8 Displacement at midspan of bridge

图9　人行桥的跨中加速度Fig.9 Acceleration at midspan of bridge

图10和图11给出了人体上下两部分m1和m2的竖向位移和加速度时程。如图所示，每一步中行人的动力响应均不同，且随着行人向跨中移动而增大。即随着行人向人行桥跨中移动，结构振动对人体的动力响应影响增加，人与结构相互作用加大。同时人体上下两部分m1和m2的动力响应也不相同。m1和m2的位移幅度接近，但是m1的位移滞后于m2。而由m1和m2的加速度局部放大图可知，m1的加速度值要大于m2。即表明人体上下两部分m1和m2的运动状态并不一致。运动中的新型双足模型即可描述人与结构相互作用的影响，又可反映人体不同部位的相对振动情况。

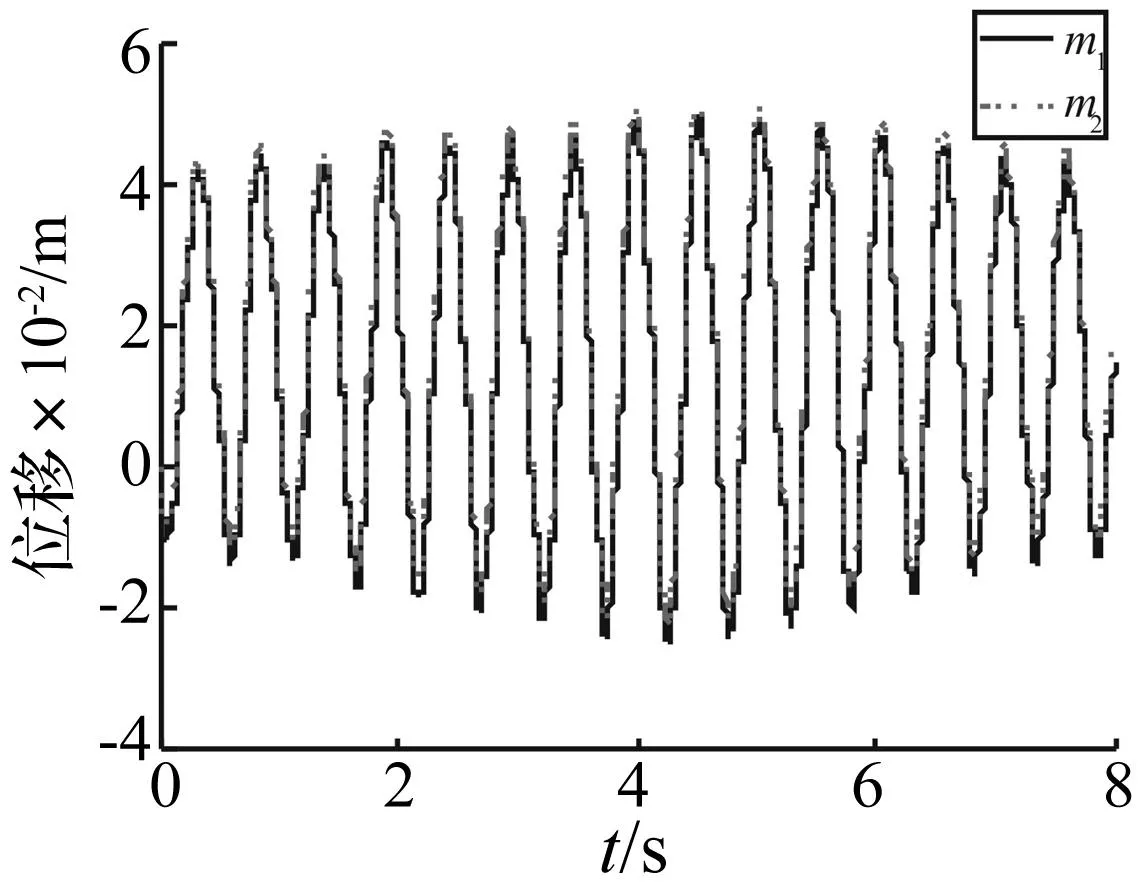
图10　m1和m2的竖向位移Fig.10 The displacement of m1 and m2

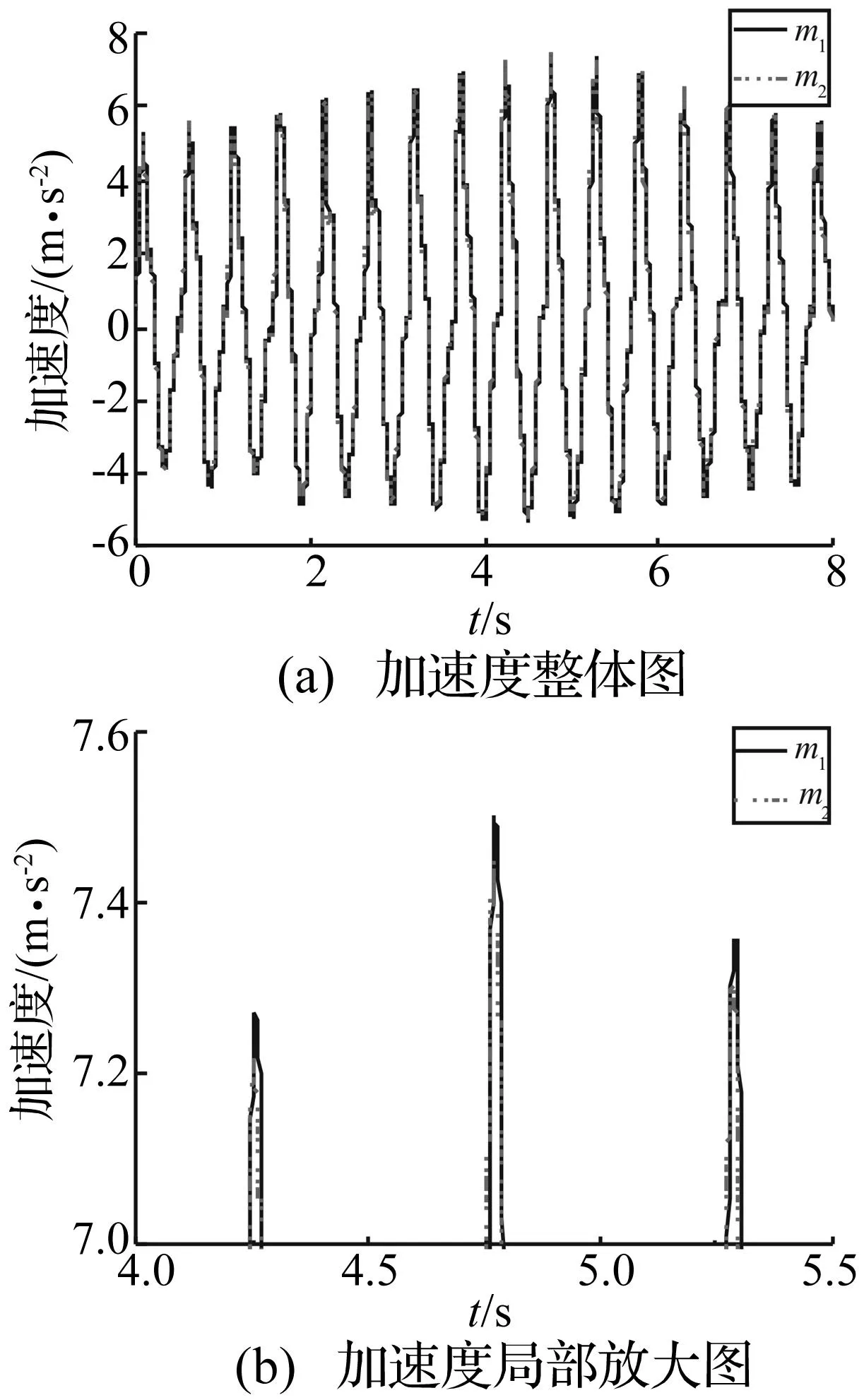
图11　m1和m2的加速度Fig.11 The acceleration of m1 and m2

在人与结构相互作用下，为研究结构振动对步行特性的影响，得出了行人步行通过结构时的竖向地面反力和行人步频(见图12和图13)。由图12可知，行人每一步产生的竖向地面反力均不同，随着行人接近跨中，结构振动响应明显，竖向地面反力将越来越大。结构振动对步行载荷产生较大影响。图13为行人步行经过人行桥与在刚性地面上行走时的步频对比。由图13可知，随着行人向跨中移动，步频变化较大，结构振动对行人步频产生影响。人的步行特性显著发生改变，人与结构之间的相互作用较明显。

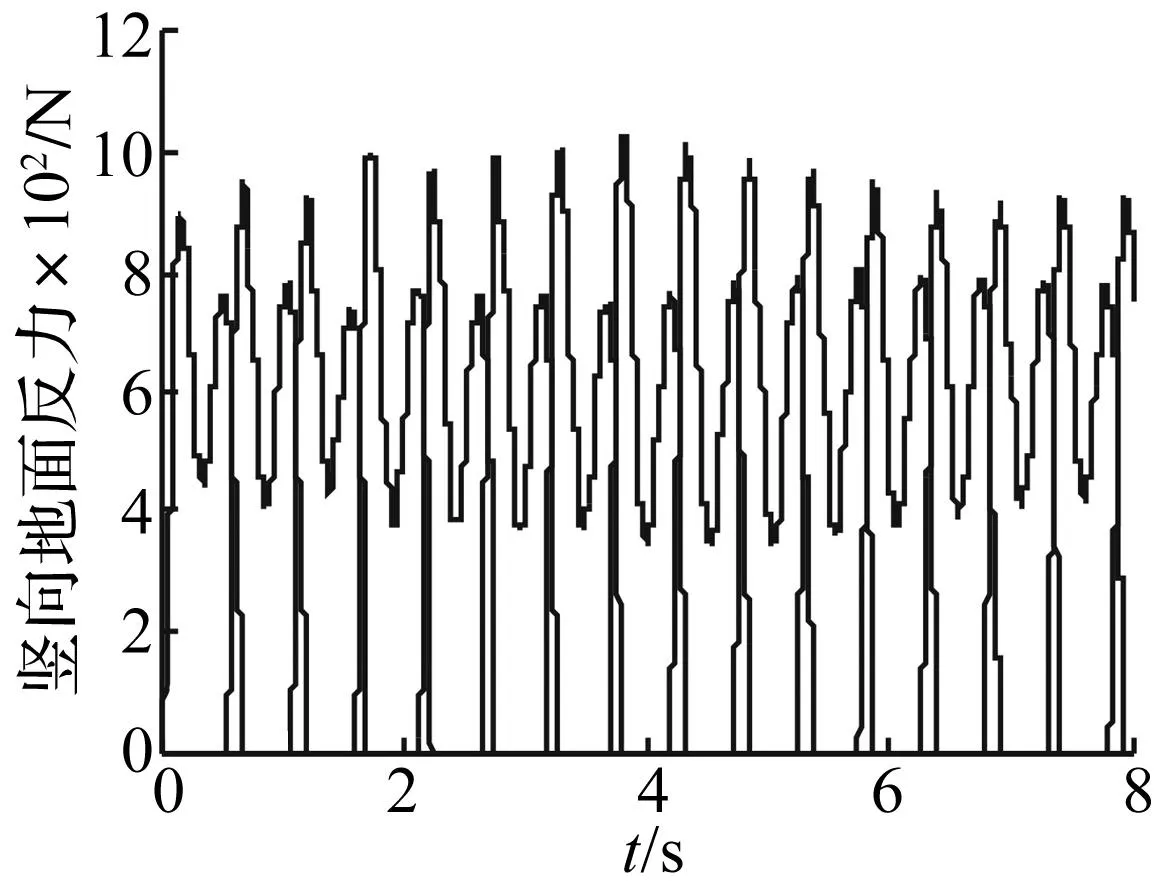
图12　步行中产生的竖向地面反力Fig.12 Vertical ground reaction force in walking

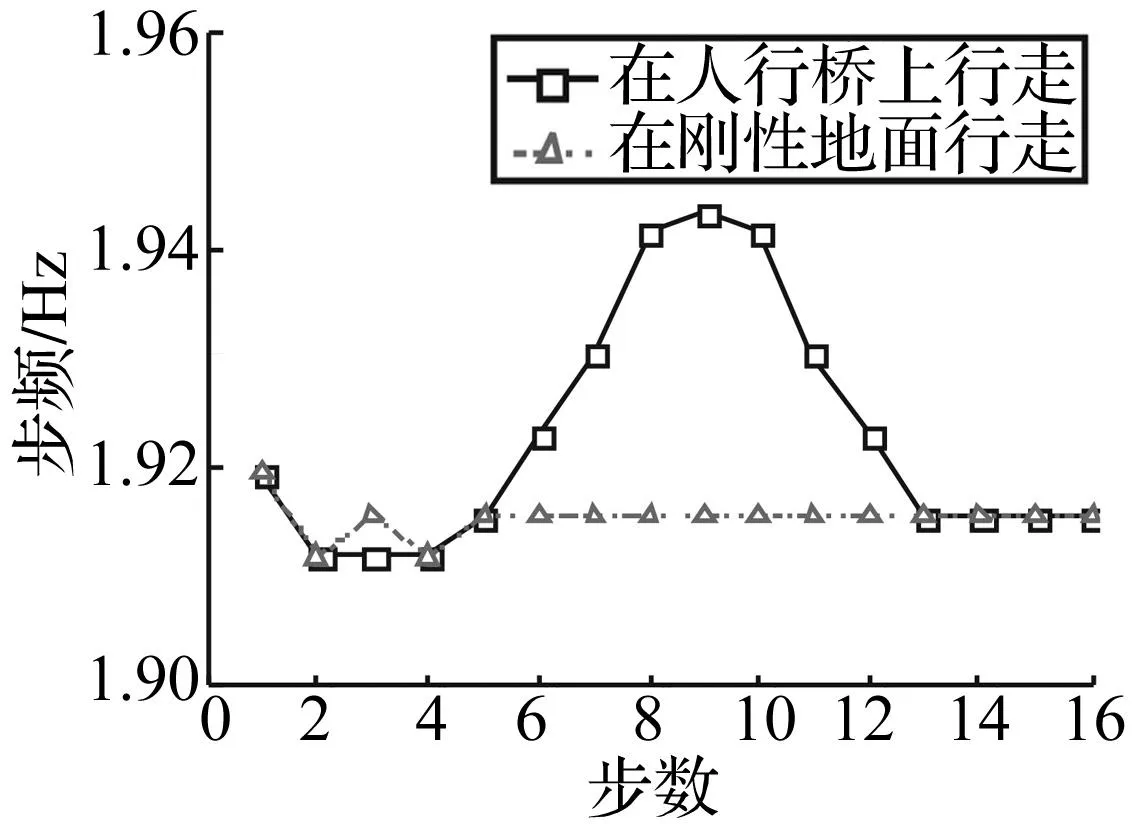
图13　步行中的步频Fig.13 Step frequencies in walking

图14为人行桥跨中的加速度谱。虚线为采用图4中竖向地面反力时程得到的结构跨中加速度谱。由于存在人与结构相互作用，新型双足模型所得的加速度谱的峰值要大于时域力模型所得，即人与结构相互作用对结构振动响应影响显著。从图14可知，加速度谱的峰值主要位于行人步频及其整数倍附近。由于人与结构相互作用下，结构振动使行人步频产生较大变化(见图13)，故新型双足模型模拟所得各峰值对应频率均大于时域力模型所得。

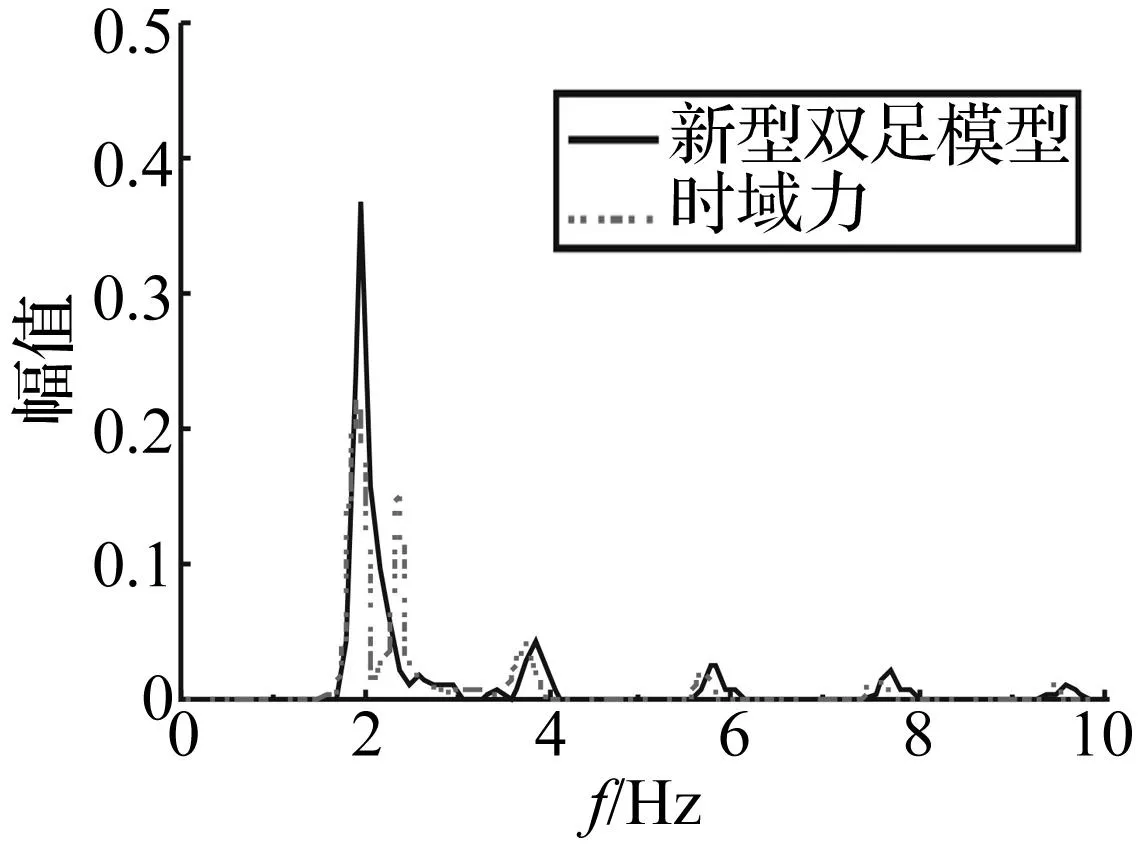
图14　人行桥跨中的加速度功率谱 Fig.14 Spectrum of acceleration at midspan of bridge

2.2结构动力特性

为研究行人对结构动力特性的影响，采用状态空间法对人与结构系统进行瞬时模态的求解，得出算例二中行人作用下柔度较大人行桥前三阶模态频率和阻尼比(见图15～图17)。人与结构系统中人行桥动力特性同时受行人步态和行人位置影响，表现为各阶模态频率降低，阻尼比增加。而其整体变化趋势主要与人的位置密切相关。对比图18中人行桥前三阶模态振型可知，当行人步行经过人行桥各模态振型的波峰时，各阶模态频率和阻尼比的变化也同时到达峰值。

以上研究表明，新型双足模型下的人与结构系统更适合研究人与结构相互作用。而时域力模型则无法考虑人受结构振动影响产生的自身行为调整及对结构振动的反馈作用，即无法描述人与结构相互作用。

图15 第一阶模态Fig.15Thefirstmodal图16 第二阶模态Fig.16Thesecondmodal图17 第三阶模态Fig.17Thethirdmodal

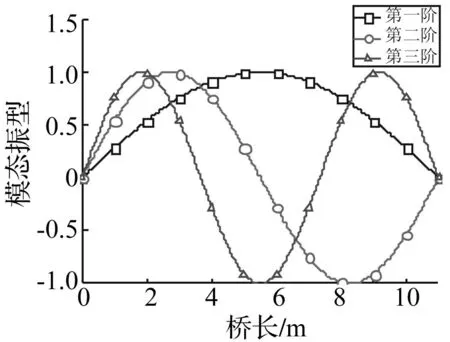
图18　人行桥的振型Fig.18 The mode shape of bridge

3人体动力特性对结构动力响应的影响

新型双足模型基于ISO 5982模型和身体由质心表示的双足模型(SDOF双足模型)，可反映人体不同部位的振动情况及其传递。为进一步分析全身振动特性对结构振动的影响，以下计算单人步行通过振动较大的梁。并将基于新型双足模型所得的分析结果与SDOF双足模型计算结果进行比较。

新型双足模型选取人体特性与前相同，SDOF双足模型选取和其一致的参数。考虑人行桥的基频与人步频接近，人行桥长为10.0 m，其余参数与算例二相同。空载桥的前两阶频率为：f1=2.169 Hz，f2=8.677 Hz。

模拟得到行人在刚性地面上单步行走时的竖向地面反力时程(见图19)。由图19可知，在相同人体参数取值情况下，新型双足模型和SDOF双足模型所得的步行载荷特性接近，所得竖向地面反力略大于SDOF双足模型。

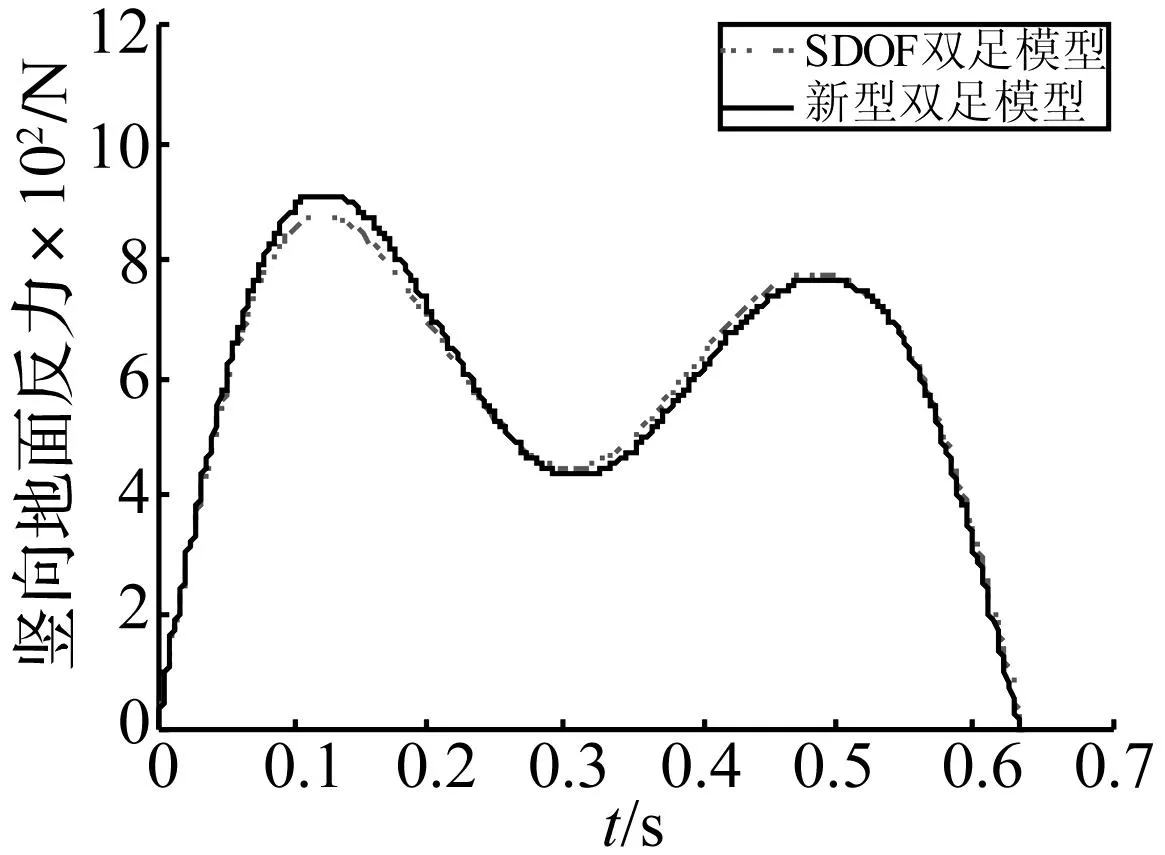
图19　单步竖向地面反力对比Fig.19 Comparison of vertical ground reaction force

图20　人行桥的跨中位移对比Fig.20 Comparison of displacement at midspan of bridge

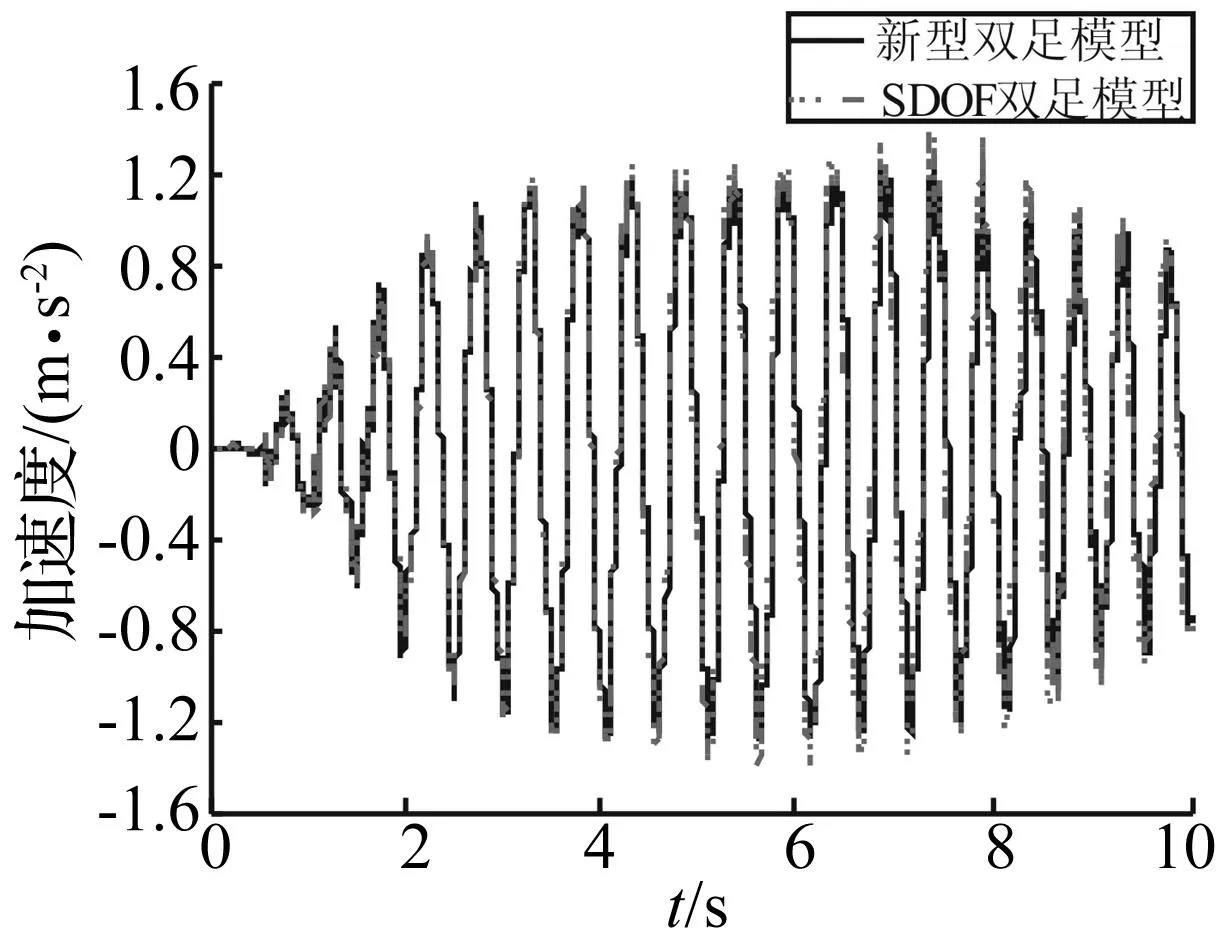
图21　人行桥的跨中加速度对比Fig.21 Comparison of acceleration at midspan of bridge

图20和图21为两种模型步行经过结构时跨中的位移和加速度。由图可知，采用SDOF双足模型所得结构振动响应要大于采用新型双足模型所得振动响应。注意到图19中，在相同人体参数取值情况下，新型双足模型所得的竖向地面反力反而大于SDOF双足模型。由此可得，结构为柔度较大结构时，振动响应较大，人体全身振动特性对结构振动响应将产生影响。

图22为两种双足模型步行时桥跨中的加速度功率谱。由图可知，由于人的步频和结构基频2.169 Hz接近，故将产生较大的振动响应，而SDOF双足模型所得结构响应显然大于考虑人体全身振动特性的新型双足模型。即人体振动特性对结构振动影响不可忽略。考虑人体全身振动特性的新型双足模型能更好的反映结构的振动响应。

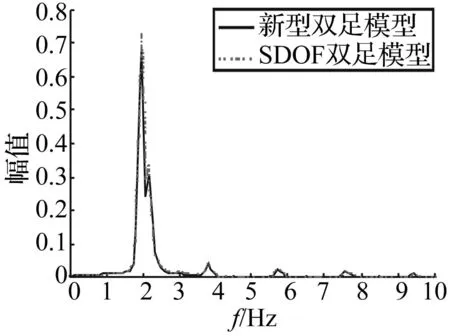
图22　人行桥跨中的加速度功率谱对比Fig.22 Comparison of spectrum of acceleration

4结论

分析了新型双足模型下的人与结构相互作用系统，得到以下主要结论：

(1) 人与结构相互作用增大结构动力响应。新型双足模型既可描述人体在振动中的动力特性，又可阐述结构振动对人的影响及人根据结构振动改变步态和动载荷，进一步增大结构动力响应的情况。

(2) 人步行经过人行桥时结构动力特性主要受人的步态和位置影响。人行桥各阶频率和阻尼比在行人位于各阶模态振型波峰时，分别达到最小值和最大值。

参 考 文 献

[ 1 ] Živanoviĉ S, Pavic A, Reynolds P. Vibration serviceability of footbridges under human-induced excitation: a literature review[J].Journal of Sound and Vibration, 2005, 279(1/2): 1-74.

[ 2 ] Sachse R, Pavic A, Reynolds P. Human-structure dynamic interaction in civil engineering dynamics: A literature review[J].Shock and Vibration Digest, 2003, 35(1): 3-18.

[ 3 ] Bachmann H, Ammann W. Vibration in structures-induced by man and machines [M]. Structural Engineering Documents No.3a. Zurich: International Association for Bridge and Structural Engineering (IABSE), 1987.

[ 4 ] Rainer J H, Pernica G, Allen D E. Dynamic loading and response of footbridges[J].Canadian Journal of Civil Engineering, 1988, 15(1): 66-71.

[ 5 ] Alexander N A. Theoretical treatment of crowd-structure interaction dynamics[J].Proceedings of the ICE-Structures and Buildings, 2006, 159(6): 329-338.

[ 6 ] 陈建英，方之楚. 人—结构相互作用动力学建模研究[J].振动与冲击，2007, 26(6): 10-13.

CHEN Jian-ying, FANG Zhi-chu. Study on modeling of human occupants-structure dynamic interaction[J].Journal of Vibration and Shock, 2007, 26(6): 10-13.

[ 7 ] 秦敬伟，杨庆山，杨娜. 人体-结构系统静态耦合的模态参数[J].振动与冲击，2012, 31(15): 150-157.

QIN Jing-wei, YANG Qing-shan, YANG Na. Modal parameters of human body-structure static interaction systems[J].Journal of vibration and shock, 2012, 31(15): 150-157.

[ 8 ] Mansfield N J, Griffin M J. Non-linearities in apparent mass and transmissibility during exposure to whole-body vertical vibration[J]. Journal of Biomechanics,2000,33(8):933-941.

[ 9 ] Matsumoto Y, Griffin M J. Mathematical models for the apparent masses of standing subjects exposed to vertical whole-body vibration[J].Journal of Sound and Vibration,2003, 260(3): 431-451.

[10] Sachse R, Pavic A, Reynolds P. Human-structure dynamic interaction in civil engineering dynamics: a literature review[J].The Shock and Vibration Digest,2003,35(1):3-18.

[11] Kim S H, Cho K I, Choi M S, et al. Development of human body model for the dynamic analysis of footbridges under pedestrian induced excitation[J].Steel Structures, 2008, 8(4):333-345.

[12] ISO 5982. Vibration and shock-mechanical driving point impedance of the human body [S]. Geneva, Switzerland: ISO, 1981.

[13] Geyer H, Seyfarth A, Blickhan R. Compliant leg behaviour explains basic dynamics of walking and running[J].Proceedings of the Royal Society B: Biological Sciences, 2006, 273(1603): 2861-2867.

[14] Whittington B R, Thelen D G. A simple mass-spring model with roller feet can induce the ground reactions observed in human walking[J].Journal of Biomechanical Engineering, 2009, 131(1): 011013—1-8.

[15] Hong H, Kim S, Kim C, et al. Spring-like gait mechanics observed during walking in both young and older adults[J]. Journal of Biomechanics, 2013, 46(1): 77-82.

[16] Kim S, Park S. Leg stiffness increases with speed to modulate gait frequency and propulsion energy[J]. Journal of Biomechanics, 2011, 44(7): 1253-1258.

[17] Wei L, Griffin M J. Mathematical models for the apparent mass of the seated human body exposed to vertical vibration[J].Journal of Sound and Vibration, 1998, 212(5): 855-874.

Structural dynamic response analysis based on a new bipedal model

WANGYi-he,YANGNa(College of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

Abstract:Based on a new bipedal model considering human dynamic characteristics, dynamic equations of human-structure interaction were established by means of Lagrange equation. Dynamic responses and interactions of human and structure were studied. The effects of human dynamic characteristics on structure vibration were also analyzed. The results showed that the human-structure interaction enhances structure vibration level the modal frequencies and damping radios of structure reach the minimum and the maximum, respectively when human walking passes the peak of each structural modal shape.

Key words:vibration; bipedal model; human-structure interaction; dynamic characteristics

中图分类号:TU311.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.005

通信作者杨娜 女，博士，教授，博士生导师，1974年生

收稿日期：2015-04-27修改稿收到日期：2015-10-08

基金项目：国家自然科学基金资助项目(51422801;50938008;51278049)；新世纪优秀人才奖励计划(NCET-11-0571)；中央高校基本科研业务费专项资金资助(2012JBM007;2012YJS078)

第一作者 王益鹤 男，博士生，1984年生