载荷作用下EPS混凝土中弹性波传播特性研究

徐松林， 方春艳， 周伟达， 郑　航， 周李姜

(中国科学技术大学 中国科学院材料力学行为和设计重点实验室，合肥　230027)



载荷作用下EPS混凝土中弹性波传播特性研究

徐松林， 方春艳， 周伟达， 郑航， 周李姜

(中国科学技术大学 中国科学院材料力学行为和设计重点实验室，合肥230027)

摘要：应用EPS混凝土模拟含缺陷的岩石材料。对EPS粒径分别为1 mm、2 mm和3 mm的三种EPS混凝土试样进行了载荷作用下不同频率的弹性波传播实验研究。采用单一频率脉冲叠合的方法来精确确定材料的波速，结果表明：EPS混凝土试件的p波波速随载荷增加的初始压密实阶段有较明显的增大趋势，当试件相对密实，波速增加则不很明显；s波波速随载荷增加有一定程度增加，但幅度比p波波速增加得小得多；应用一种相对波速的方法，即将波速与当前载荷下材料的声波速度进行对比，可以较好地分析波速与载荷及频率的关系；最后对波速与载荷和频率的关系进行了理论模拟分析。此研究对于应用弹性波进行材料和结构的无损检测等技术方面有参考意义。

关键词：弹性波；EPS混凝土；载荷作用；P波；S波

EPS混凝土是将发泡聚苯乙烯(Expanded Polystyrene)颗粒作为轻质骨料加入到混凝土中制作得到的一种节能型建筑材料[1]，其宏观力学性能是混凝土基体部分和EPS颗粒共同作用的结果。本文进行载荷作用下EPS混凝土中弹性波传播特性研究的目的是将EPS混凝土作为岩石试件的模型材料，以研究含缺陷岩体中弹性波传播规律。混凝土基体的力学性能与岩石比较接近，可模拟岩石材料部分；EPS颗粒非常软且轻，其弹性参数远低于混凝土基体材料，可模拟岩石中所含孔洞等缺陷或软弱填充物。这样，通过调整EPS颗粒的尺寸可得到含不同尺寸的缺陷的模型材料。含不同尺寸EPS颗粒的混凝土试样弹性波传播特性存在一定的差异，这种差异反映出材料内部几何结构的变化对弹性波传播规律的影响。载荷作用也可使材料内部结构发生变化，引起弹性波传播特性的变化。产生这种变化的实质是弹性波与不同几何结构的相互作用。

岩石由不同成分的矿物颗粒组成的骨架以及内部存在的不同尺寸的节理、裂纹和孔洞形式的缺陷构成[2-3]。自然界中存在的岩体处在复杂的地应力状态下，岩体内缺陷处于一定程度的张开或闭合状态，这些复杂的状态必然影响到岩石材料的宏观物理力学参数，表现出强烈的波速和衰减对频率的依赖性[4-5]。声波和地震波是水利工程、岩土工程等测试规范和规程中测试现场岩体性质，进行岩体完整性评价和岩体质量评价的主要依据。这两种技术的实质就是利用弹性波作为“尺子”对岩石类材料中的缺陷进行定量测量[6-8]。岩石类材料局部的弹性波速度与当地应力状态、加卸荷过程及测量体的尺寸相关，这使得现场声波和地震波测试结果非常复杂。进行复杂材料中弹性波传播规律的研究，就是要认识波速、载荷与岩体内部结构的关系，逐步建立三者的定性和定量联系[9-10]。

一般而言，地应力水平越高，现场测试得到的声波速度越高。Winkler[11]探讨了水平应力对岩体波速的影响。Savich等[12-13]总结现场地应力和地震波测试资料，提出用微震声学法研究岩体原始应力场。刘高[14]研究小观音坝现场岩体弹性波，总结了地应力与弹性波速度的关系。Gret等[15]在矿山开采过程中进行了类似探索。这些都是基于现场测试结果进行简单的数据总结。王晓杰等[16]将“正交偶极阵列”分析方法应用于声波测井技术中，提出利用现场测试的快慢横波来确定当地的最大和最小主应力。但是，要真正建立波速与载荷(应力、地应力等)的关系，须以岩石细观结构作为桥梁。因此，探索岩体中几何结构对波传播的影响显得尤为重要。邓向允等[17-18]采用人工预制裂纹，对含多种裂纹组合的玄武岩试件进行多种频率的实验室声波研究，讨论了不同缺陷组合下声波传播特性，并初步研究了载荷作用的影响。现有研究已经证实：岩体几何结构与波速有着重要的联系。籍此，研究载荷作用下岩体结构与波速的变化，可逐步建立应力-岩体结构-波速三者的关系。Sinha等[19-20]，Liu等[21]对含孔洞的岩体在压力作用下的弹性波特性进行了研究。Chapman[22-23]研究了孔隙流体压力作用下孔洞产生裂纹过程岩体中弹性波波速随频率的变化。基于Achenbach等[24-25]的工作，本实验室较系统地研究了裂纹、孔洞等细微观结构，及其组合对弹性波传播的影响。这些研究加深了对复杂介质中弹性波传播特性的理解。但是，对于应力-岩体结构-波速三者的关系尚没有很好的研究结果。

因此，本文将以EPS混凝土为模型材料，进行不同载荷和不同频率下声波测试，研究载荷和频率对弹性波传播的影响，并基于文献[27]中所提出的无量纲分析方法，探讨载荷的影响。

1声波实验

1.1实验设备

载荷对弹性波波速的影响实验在中国科学技术大学工程实验中心MTS810试验系统上进行(见图1)。特制的发射探头和接收探头分别埋设在上下两个承压筒内，按图1所示，将这两个承压筒分别放置在试样的上下两个端面。当试验机进行加载的时候，承压筒传递载荷，同时保护好其内部的声波探头。这样，就可以实现在加载过程中同时对样品进行加载方向的声波测试。

主要进行3种频率的测试。采用岩海RST01C声波仪，其中心频率为25 kHz，时间分辨率0.2 us。声波探头为平面探头，发射探头含有一个纵波压电陶瓷传感器，发射纵波，三种发射探头的主频分别为；50 kHz、300 kHz和1 MHz；与之对应有三种接受探头，其中心频率与发射探头对应。接收探头含有一个纵波(p)压电陶瓷传感器和两个横波(s1、s2)压电陶瓷传感器，接收p波和s波。由此，通过改变轴向压力分别测试记录每一级载荷下，对应的纵波波速Cp和两个横波波速Cs1、Cs2。

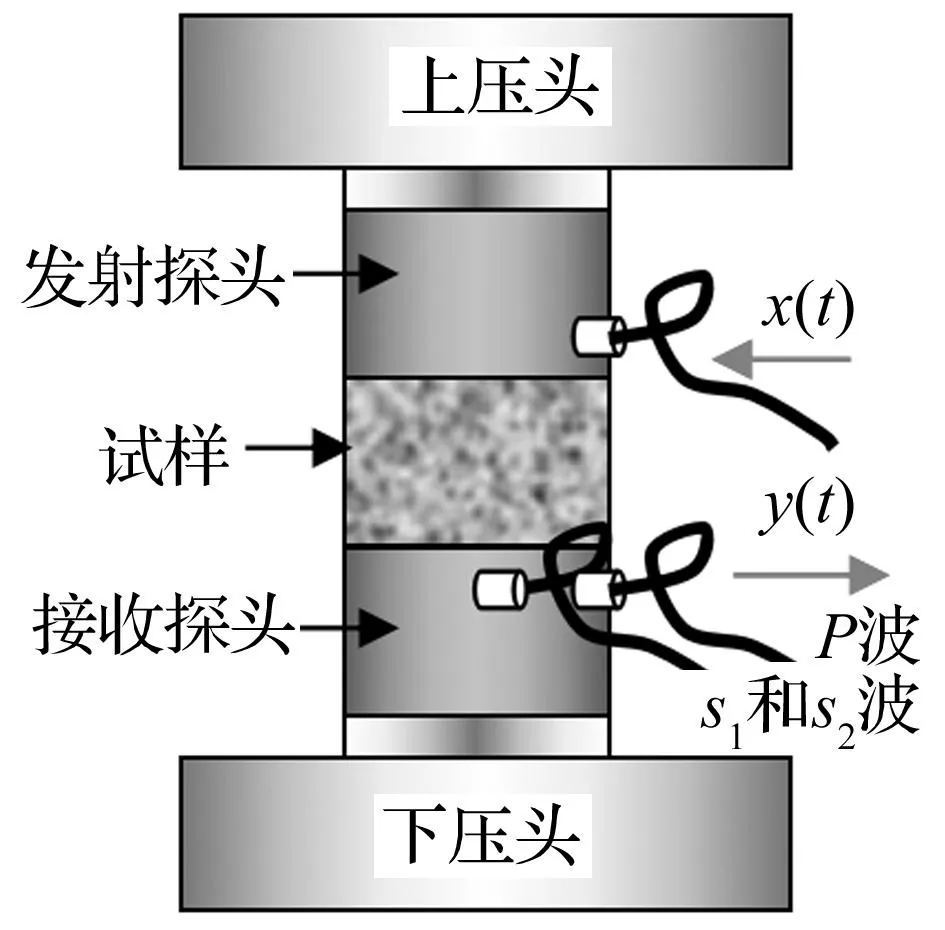
图1　载荷作用下声波测试示意图Fig.1 Schematic diagram ofacoustic measurement of sample under loading

1.2EPS混凝土试件及实验步骤

EPS混凝土按每立方混凝土中水泥、水、石、砂的重量分别为：570 kg、154 kg、793 kg、669 kg进行配比。其中，水泥为强度等级42.5的普通硅酸盐水泥，粗骨料为直径5～10 mm的石子，细集料为细度模数为2.5的河沙。采用聚羧酸高效减水剂。由此制得混凝土的基体密度为2.446 g/cm3，单轴抗压强度为110 MPa，弹性模量为34 GPa。EPS混凝土是在此混凝土的基础上添加一定体积的粒径为1 mm或3 mm的EPS颗粒，可分别制得EPS颗粒体积率为10%～40%的EPS混凝土。具体制作方法和样品物理力学特性，以及样品的动静态力学性能可参见文献[1]。本文研究选用试件具体参数见表1。试件加工成直径约69 mm，厚度约35mm的圆柱。EPS混凝土的声波速度较低，此试件厚度对于主频为300 kHz和1 MHz的实验比较合适，但是对于主频为50 kHz的实验须具体分析，此时波长与试件尺寸比较接近，须采用Rayleigh散射理论进行讨论。

表1　EPS混凝土试件

注：EPS体积率=1-EPS混凝土密度/混凝土密度(2.446 g/cm3)

实验前，在没有载荷作用的情况下，测量试件的p波和s波波速。然后按图1的示意，组装试件和探头。在发射探头和接收探头中间放试件，试件和探头间垫厚度约3 mm的铅片。若试件表面平整度非常好，而且与声波探头之间配合很好，可只添加凡士林作为耦合剂来测试P波。但是，采用凡士林作为剪切波耦合剂测试S波，会造成较大的衰减；需用特殊的耦合剂，如Sonotech的shear Gel或Olmpus的shear wave complant等。因为有载荷作用，用铅做垫片一般可以得到较好的s波。发射探头接声波仪和示波器CH1，可在计算机上显示入射波波形，便于对比分析；示波器的Cp、Ch1和Cp分别连接接收探头的p波、s1波和s2波接头。安装好后，采用MTS实验系统控制加载。每加载一定载荷，记录一次载荷与位移的数据，并相应保存入射波以及p波、s1波和s2波波形。加载到设定载荷，共记录15～20组数据(每一级载荷按设计记录数据总的组数进行划分)。然后卸载，每一级卸载荷荷基于相应的加载级别进行，记录载荷与位移的数据和保存入射波以及p波、s1波和s2波波形，直到完全卸载。然后换另一种频率的探头重复上述过程。

1.3实验波形及波速确定方法

图2所示为示波器记录的测试波形。由图2可知：① 由于EPS混凝土内部几何结构比较复杂，含有一定粒径(如1 mm或3 mm)的EPS颗粒、直径5～10 mm的石子等，这些结构的尺寸与入射波的波长处于比较接近的量级，容易引起波的频散，因此，p波和s波的波系结构也比较复杂；② 由于这些复杂的材料结构，材料内部传播的波很难有单纯的p波和s波存在，几乎所有的波都是p波和s波的耦合作用，因此，当p波探头测试到信号时，两个s波探头也测到信号，这种s波探头探测到的早到的信号实际上是一种由于材料内部复杂结构引起的p波和s波的耦合效应。图中s2波幅值很小可能因为材料具有一定的各向异性。随着载荷的增大，s2波幅值逐渐增大。

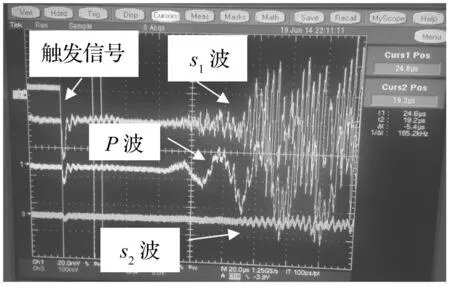
图2　声波测试波形Fig.2 Recorded wave profiles of sonic test

一般通过确定波到来的时间来计算相应的波速。但是，从上述波形来看，准确确定波到来的起跳点很困难。虽然入射波是由主频为50 kHz、300 kHz或1 MHz的发射探头发射的，但是，入射波仍然是一种含有多种频率的波，只不过除主频外，其他频率的波对应的幅值较小而已。接收探头接收到的波也一样，也是含多种频率的复合波，而且它比入射波更复杂。这是因为在入射波传播过程中，波要与材料中的细微观结构发生相互作用，即发生所谓的散射作用，从而产生具有一定频率分布的复杂波系。因此，波形的起跳点是很难准确确定的。为解决此问题，Li等[28-30]在采用超声波技术进行高温高压作用下矿物的弹性参数测试中，提出了一种非常有效的脉冲比对法(pulse echo overlap method, PEO)。其核心思想是：找出单一频率的入射信号和对应的单一频率的透射信号或反射信号脉冲，然后进行比对。

如图1所示，发射探头发射的入射波信号为x(t)，接收探头接收到的信号为y(t)。若试件系统的响应为h(t)，则它们满足关系式：y(t)=x(t)*h(t)，即接收到的信号y(t)为入射波信号x(t)与系统响应h(t)的卷积。对其进行快速傅里叶变换(Fast Fourier Transform Algorithm,FFT)，可以得到：Y(f)=X(f)H(f)，其中f为频率。因此，试件系统的响应：H(f)=Y(f)/X(f)。

若实验中设定入射信号x(t)为正弦波，则其傅里叶变换值为1，由此，有：Y(f)=H(f)。这表明：在频率域，此情况下的系统响应与接收到的信号相同。因此，反过来对入射信号的FFT和传递函数进行卷积可以得到系统的响应。基于此思想可以重建主频附近区域任意单一频率的信号传播的过程，然后由此确定此频率下材料的波速。图3(a)为对测试波形进行300 kHz (5个周期)卷积后重构得到的波形图，图3(a)中所示频率为300 kHz 5个周期组成的脉冲信号的传播。为确定传播时间，将后面的脉冲前移，与前面的脉冲信号进行覆盖比较，(见图3(b))。找到最佳覆盖模式，对应的时间差即为频率为300 kHz的波的传播时间。由此可以准确地计算波速。重复此过程，可以计算多种频率下波的传播速度。

图3　载荷作用下声波测试示意图Fig.3 Schematic diagram ofacoustic measurement of sample under loading

2实验结果

图4所示为采用上述方法得到不同频率下的p波(见图4(a))和s波(见图4(b))随载荷变化的关系曲线。由图4(a)可知：随着外载荷的增大，p波波速开始阶段有较明显的增加，这表明此过程EPS混凝土有较大的压缩量，逐渐处于更加密实的状态；当外载荷增加到4 MPa，p波波速有一定的增加，但不是很明显，说明EPS混凝土试件此时处于密实状态。图4(b)所示的s波也有相似的规律,比较而言，在弹性波测试中，p波比s波对外载荷更敏感。图4中卸载过程的波速要比加载过程的略高，主要因为材料压实后通过卸载回复到原来的状态需要较长的时间，因此，对比加载和卸载过程，在同样载荷下，试件在卸载过程尚处于压实状态，波速相对较高。比较不同载荷下加卸载过程可以分析材料内部微观结构的变化，这将在以后基于微力学的方法进行研究。

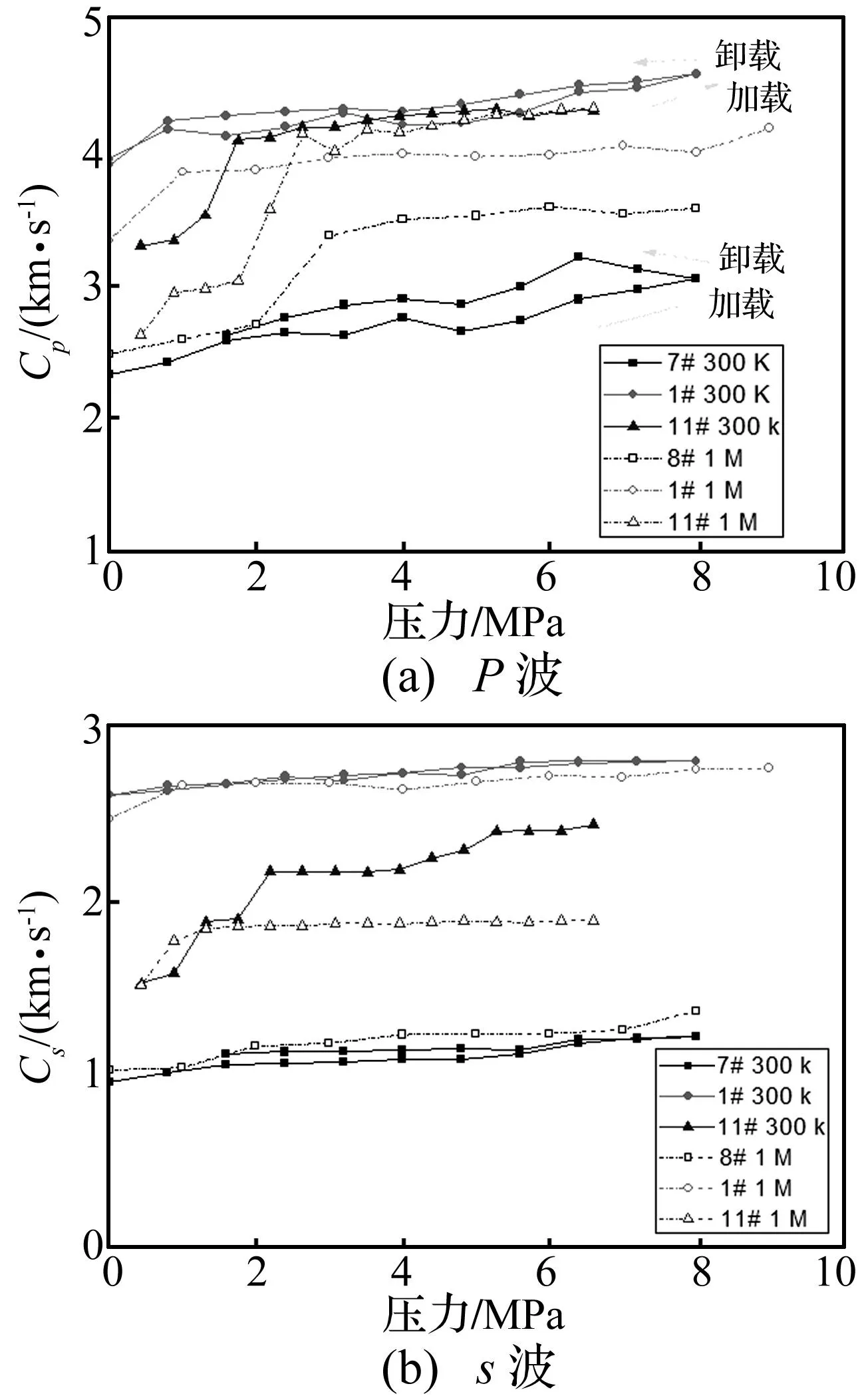
图4　EPS混凝土波速与压力的关系Fig.4 Relationship of wave speed to pressure of EPS concrete

图4中所示有四个试件的数据，即1#试件和11#试件的300 kHz和1 MHz,7#试件的300 kHz和8#试件的1 MHz的数据。原计划进行分析的50 kHz的实验，由于入射波波长相对较长而试件相对较短，分析得到的数据比较复杂，因此，未纳入讨论。7#和8#试件在进行实验的后期，试件均有一定程度的变形和损坏，因此只能进行一种频率的加载，而无法进行多种频率的多次加载对比实验；但是由于这两个试件密度相当、EPS颗粒尺寸一样，而且其压缩过程也比较接近(见图5)，因此，这两个试件可作为同一种材料两种频率的对比分析。比较EPS颗粒粒径为1 mm的1#试件和颗粒粒径为3 mm的7#和8#试件的实验结果，无论p波波速或s波波速，1#试件要比7#和8#试件高得多。这主要源于1#试件中EPS颗粒的体积率要小得多。

而EPS颗粒粒径为2 mm的11#试件实验结果相对比较复杂。在加载的开始阶段，其波速较靠近具有较高孔隙度的7#和8#试件；随着外载荷的增加，波速很快上升到与低孔隙度的1#试件较接近。这种中间孔隙度试件的波速变化过程在某种程度上反映了加载过程中孔隙体系的某种演化特性，需要深入研究。

理论上，弹性波的频率越高，测试得到的材料的波速越高，这就是所谓的“频散效应”。作为对比的7#和8#试件的p波和s波波速都反映了这一趋势。但是，实际测试得到的1#试件和11#试件的波速与此规律并不一致：频率1 MHz时测试得到的波速反而低于频率300 kHz时的数值。其原因在于：这两个试件的频率1 MHz的实验在频率300 kHz实验之前，进行300 kHz实验时，试件实际上已经进行过一次较大峰值应力的加卸载过程(如1#试件的9 MPa、11#试件的6.6 MPa)，相当于材料进行过一次压实，因此，300 kHz实验时的波速相对较高。频率1 MHz的实验(图5中空心标记线)和频率300 kHz的实验(图5中实心标记线)中试件压缩过程曲线见图5，两次压缩过程存在一定差异，表现出明显的压实特性。因此，为了更好地分析波速数据，现提出一种相对波速的方法，即将波速与当前试件的压缩状况进行联系而对比分析。

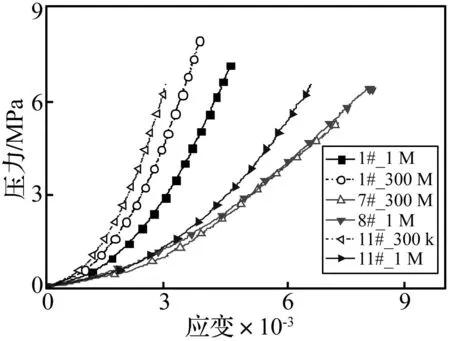
图5　EPS混凝土压缩过程Fig.5 Compression of EPS concrete

图6　波速比与压力的关系Fig.6 Relationship of speed ratio to pressure

另外，上一节讨论的基于实验数据进行多种单一频率的波速的分析问题，可以进行尝试。但由于EPS混凝土试件的微观结构非常复杂，得到的结果并不是很理想。主要表现在：① 与入射波主频对应的信号的幅值很好，但是，分解出来的主频附件的其他频率的幅值很小；② 从透射波中分离出主频对应的信号的幅值很好，而分离出的主频附件的其他频率的波的幅值不稳定，时大时小，大的时候甚至超过对应频率的入射波，这明显与波的传播规律相矛盾。产生此现象的原因是：入射波要与材料内部的微观结构发生相互作用，由此要产生具有一定频率分布的波系。这就是所谓的“散射”现象。由此，透射波中分离出的某一频率的波与入射波中并不一定有必然的对应关系，可能是入射波中其他频率的波散射产生的。相关问题需要进行较深入的研究。

3波速与载荷和频率关系的探讨

文献[27]基于量纲理论分析方法，得到一个关于波速的半理论公式，其表达式为：

(1)

式(1)中有三个参数，即Φ、D0和Cu，它们都与实际材料中所含的缺陷有关，都是与压力有关的参数。基于式(1)进行波速与载荷关系的讨论，实际上是研究这三个参数与载荷的关系。因为有图5的压缩过程曲线，因此，Φ、D0和Cu等三个参数可结合压缩过程曲线确定。Φ、D0随载荷的变化，根据对应载荷下的应变计算，这里忽略横向应变(孔隙率较大的材料其宏观泊松比趋向于0)。Cu由压缩曲线的切线斜率计算。由此，对1#试件进行模拟分析，得到波速与频率的关系如图7所示。图中纵坐标为基于不含EPS颗粒的混凝土的波速进行归一化后的相对波速。

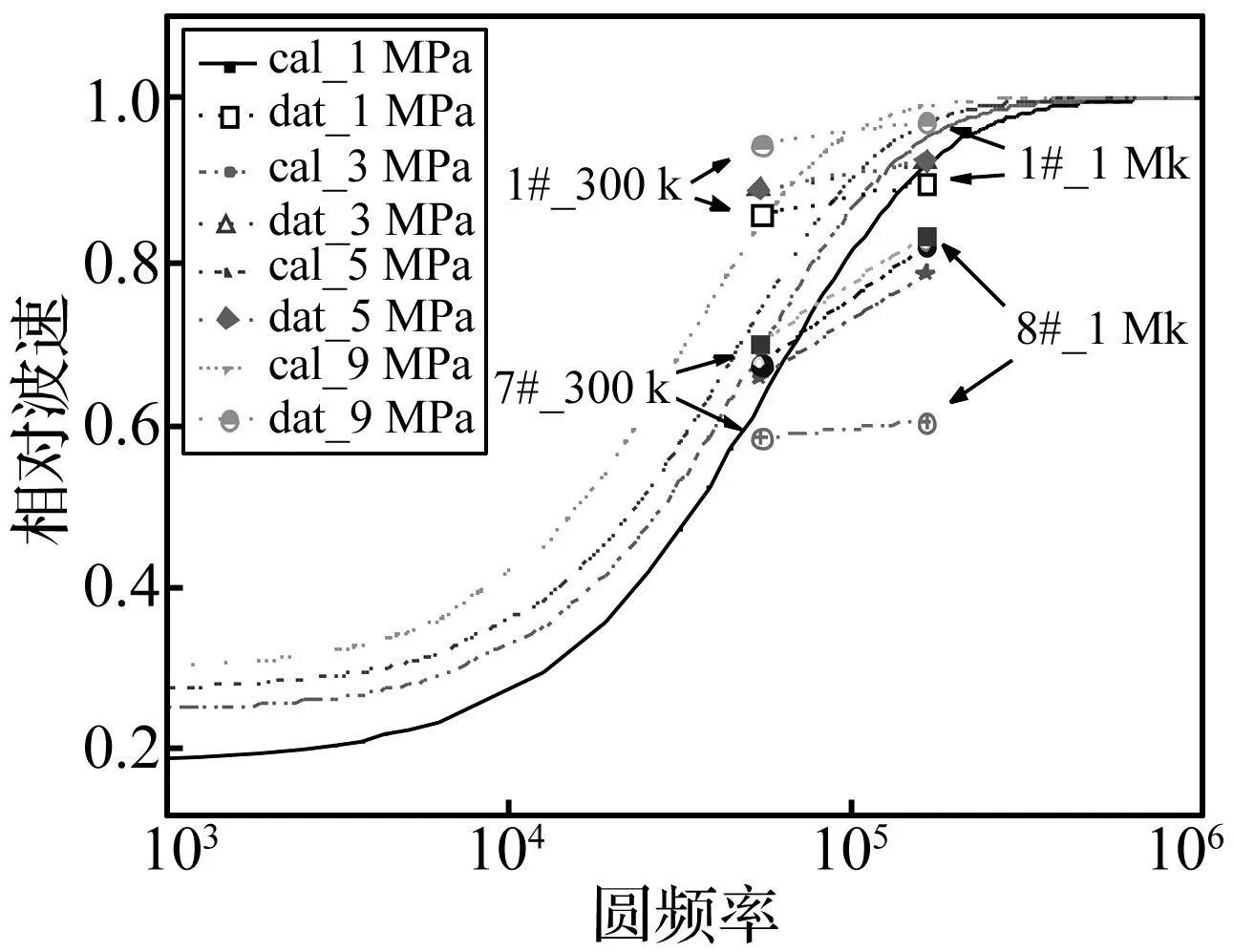
图7　波速与频率的关系(1#试件)Fig.7 Relationship of normalized speed to frequency of sample #1

图7中所示模拟结果表明：波速随频率增加而明显增加。但是这种趋势只发生在一个区段，此区段对应材料的共振区域，包含与较高波速对应的米氏(Mie’s)散射和与较低波速对应的瑞利(Rayleigh)散射。此区段之外，对应较高波速的是射线理论描述的区域，而较低波速对应的是等效介质理论描述的区域。EPS混凝土试件的300 kHz和1 MHz的实验数据基本处于此共振区域，材料的波速对频率和外载荷都比较敏感，应用弹性波来研究其微观结构响应比较合适。7#和8#试件的数据作为参照，它们反映的是另一个跨度更大、中心频率更低的共振区域的数据，这个区域的中心频率与7#和8#试件中EPS颗粒粒径有关。

另外，图7表明：模拟结果能反应较好的定性规律，但是与实验数据的对比则反映出模型尚无法进行较全面的定量描述。其原因在于：式(1)中关于材料的结构只采用了两个参数Φ、D0进行描述，它们反应的是材料结构的一种平均效应。文献[7]的计算结果表明：考虑材料内细微观结构的分布特性是非常必要的。因此，更深入的模拟分析需要结合加载过程中细观结构的分布和相应的演化过程进行。此时，材料的微观结构的描述至少需要三类参数，即平均缺陷尺寸、缺陷的分布、缺陷的张开和闭合状态等。相关工作将另文探讨。

4结论

为研究含缺陷的岩石中弹性波传播特性，以EPS混凝土为模型材料，对EPS颗粒粒径为1 mm、2 mm和3 mm的三类EPS混凝土进行了载荷作用下不同频率的弹性波传播特性实验，对比研究了三类EPS混凝土的p波和s波波速及相关波传播特性。并应用基于无量纲理论的公式进行了波速与载荷和频率关系的探讨。得到的主要结论如下：

(1) p波波速随载荷增加在开始加载阶段有较明显的增大趋势；当试件相对密实，波速增加不明显。s波波速有相同的增加趋势，但波速增加幅度比p波波速增加的小得多。

(2) 单一频率脉冲叠合方法(PEO)是一种可以准确确定复杂材料波速的方法。但受EPS混凝土试件内复杂细微观结构的影响，本文只能进行主频率的分析，而进行主频率附近其他单一频率的分析，需要进一步的研究。

(3) 将波速与当前试件的声波波速进行联系而对比分析的相对波速方法可以用于研究非线性压缩过程中复杂材料的波速与载荷和频率的关系。此相对波速可以实时反映材料微观结构的状态，及其对动载荷的响应特征。

(4) 应用基于无量纲理论的公式进行了波速与载荷和频率关系的模拟分析。模拟结果表明此分析方法在定性上是可行的，但是，进行较可靠的定量分析，还需要引入缺陷尺寸、缺陷尺寸的分布特征以及缺陷的张开和闭合状态等参量。需要结合一定的微观几何结构的调查工作。

参 考 文 献

[ 1 ] 胡俊，巫绪涛，胡时胜. EPS混凝土动态力学性能研究[J]. 振动与冲击，2011,30(7):205-209.

HU Jun, WU Xu-tao, HU Shi-sheng. Dynamic mechanical behavior of EPS concrete[J]. Journal of Vibration and Shock, 2011, 30 (7): 205-209.

[ 2 ] 席道瑛,徐松林,编著，岩石物理与本构理论[M]. 合肥:中国科学技术大学出版社, 2016.

[ 3 ] 席道瑛,徐松林,编著, 岩石物理学基础[M]. 合肥:中国科学技术大学出版社, 2012.

[ 4 ] 席道瑛，徐松林，刘永贵,等，饱和砂岩的滞弹性弛豫衰减特征及微观机理的探索[J]. 物理学报，2012, 61(14)：149101-1-8.

XI Dao-ying，XU Song-lin, LIU Yong-gui, et al，Viscoelastic relaxation attenuation property for saturated sandstones and corresponding investigation on micro-scale mechanism[J]. Acta Physica Sinica, 2012， 61(14)：149101-1-8.

[ 5 ] 席道瑛，徐松林，杜赟.泵油饱和砂岩的粘弹行为的实验研究[J]. 物理学报，2012， 61(11)：119102-1-7.

XI Dao-ying，XU Song-lin, DU Yun.Experimental research on viscoelastic behavior for pump-oil saturated sandstones[J]. Acta Physica Sinica, 2012, 61(11)：119102-1-7.

[ 6 ] 徐松林，刘永贵, 席道瑛，等，弹性波在含双裂纹岩体中的传播分析[J]. 地球物理学报，2012,55(3)：944-952.

XU Song-lin, LIU Yong-gui, XI Dao-ying, et al. Analysis of the propagation of elastic wave in rocks with double-crack model[J]. Chinese Journal of Geophysics,2012,55(3)：944-952.

[ 7 ] 谭子翰，徐松林，刘永贵，等，含多种尺寸缺陷岩体中的弹性波散射[J]. 应用数学和力学，2013, 34(1): 38-48.

TAN Zi-han, XU Song-lin, LIU Yong-gui, et al, Scattering of elastic waves by multi-size defects in rock mass[J].Applied Mathematics and Mechanics,2013,34(1):38-48.

[ 8 ] 罗松南,程红梅,童桦. 混凝土结构中钢精对波传播的影响分析[J]. 振动与冲击，2006,24(4): 66-68.

LUO Song-nan, CHENG Hong-mei, TONG Hua. Analysis of effects of reinforced steel bar on wave propagation in concrete media[J].Journal of Vibration and Shock,2006,24(4):66-68.

[ 9 ] 徐松林，刘永贵，席道瑛,等. 卸荷过程岩体中弹性波波速变化分析[J]. 岩土力学，2011，32(10): 2907-2915.

XU Song-lin, LIU Yong-gui, XI Dao-ying, et al. Analysis of variation of elastic wave velocity in rock mass under unloading condition[J]. Rock and Soil Mechanics, 2011，32(10): 2907-2915.

[10] 刘永贵，徐松林，席道瑛，等.节理玄武岩体弹性波频散效应研究[J]. 岩石力学与工程学报，2010，29(增刊1)：3314-3320.

LIU Yong-gui, XU Song-lin, XI Dao-ying, et al. Dispersion effect of elastic wave in jointed basalts[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(Sup1)：3314-3320.

[11] Winkler K W. Frequency dependent ultrasonic properties of high-porosity sandstones[J]. Journal of Geophysical Research: Solid Earth, 1983, 88(Sup1): 9493-9499.

[12] Savich A, Razumov V, Khositashvili G, et al. Refinement of the engineering-geological conditions of the foundation of the Khudoni arch dam[J]. Hydrotechnical Construction,1990, 24(2): 122-130.

[13] Savich A. Long-term geophysical observations at hydrotechnical construction sites[J]. Power Technology and Engineering:formerly Hydrotechnical Construction,1993, 27(3): 123-130.

[14] 刘高, 谌文武, 梁收运, 等. 小观音坝址区岩体弹性波特征及其应用[J]. 岩石力学与工程学报, 2003,22(2):2819-2823.

LIU Gao, SHEN Wen-wu, LIANG Shou-yun, et al. Charateristics of elastic wave and its application to Xiaoguanyin dam site on Yellow river[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 2819-2823.

[15] Grêt A, Snieder R, Özbay U. Monitoring in situ stress changes in a mining environment with coda wave interferometry[J].Geophysical Journal International,2006,167(2):504-508.

[16] 王晓杰，楚泽涵，柴细元，等. 用正交偶极子声波测井资料估算地层应力场[J]. 测井技术. 2004, 28(4): 285-288.

WANG Xiao-jie, CHU Ze-han, CAI Xi-yuan, et al. Estimating formation stress from cross 2 dipode acoustic measurement[J].Well Logging Technology,2004,28(4):285-288.

[17] 邓向允，徐松林,李广场，等. 缺陷对玄武岩中声波波速影响的试验研究[J]. 实验力学，2009，24(1)：13-20.

DENG Xiang-yun, XU Song-lin, LI Guang-chang, et al. Experimental study of defect effect on sonic velocity in basalt[J]. Chinese Journal of Experimental Mechanics, 2009，24(1)：13-20.

[18] 邓向允，徐松林,李广场，等. 玄武岩中裂隙分布形式对声波传播的影响[J]. 实验力学，2009，24(5)：421-426.

DENG Xiang-yun, XU Song-lin, LI Guang-chang, et al. Study of crack distribution effect on sound wave propagation in basalt[J]. Chinese Journal of Experimental Mechanics, 2009，24(5)：421-426.

[19] Sinha B K, Kostek S, Norris A N. Stoneley and flexural modes in pressurized boreholes[J]. Journal of Geophysical Research: Solid Earth (1978-2012),1995, 100(Sup1): 22375-22381.

[20] Sinha B K, Liu Q H, Kostek S. Acoustic waves in pressurized boreholes: A finite difference formulation[J]. Journal of Geophysical Research,1996, 101(Sup1): 25173-25180.

[21] Liu Q H, Sinha B K. A 3D cylindrical PML/FDTD method for elastic waves in fluid-filled pressurized boreholes in triaxially stressed formations[J]. Geophysics,2003, 68(5): 1731-1743.

[22] Chapman M, Zatsepin S V, Crampin S. Derivation of a microstructural poroelastic model[J]. Geophysical Journal International,2002, 151(2): 427-451.

[23] Chapman M. Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity[J]. Geophysical Prospecting,2003, 51(5): 369-379.

[24] Achenbach J D, Gautesen A K, McMaken H. Ray methods for waves in elastic solids: with applications to scattering by cracks[M].Pitman Advanced Pub. Program,1982.

[25] Zhang C, Achenbach J. Scattering by multiple crack configurations[J]. ASME, Transactions, Journal of Applied Mechanics,1988, 55: 104-110.

[26] 谭子翰. 复杂岩体中弹性波的频散和衰减规律研究[D].合肥：中国科学技术大学，2013.

[27] 徐松林，郑文，刘永贵,等. 岩体中弹性波传播尺度效应的初步分析[J]. 岩土工程学报，2011, 33(9): 1348-1356.

XU Song-lin, ZHENG Wen, LIU Yong-gui, et al. A preliminary analysis of scale effect of elastic wave propagation in rock mass[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1348-1356.

[28] Li B, Chen K, Kung J, et al. Sound velocity measurement using transfer function method[J]. Journal of Physics: Condensed Matter, 2002, 14:11337-11342.

[29] Li B, Kung J, Liebermann R. Modern techniques in measuring elasticity of earth materials at high pressure and high temperature using ultrasonic interferometry in conjunction with synchrotron X-radiation in multi-anvil apparatus[J]. Physics of the Earth and Planetary Interiors,2004,143/144:559-574.

[30] Li B, Liebermann R. Study of the Earth’s interior using measurements of sound velocities in minerals by ultrasonic interferometry[J]. Physics of the Earth and Planetary Interiors, 2014, 233:135-153.

Elastic wave propagation in EPS concrete under loadings

XUSong-lin,FANGChun-yan,ZHOUWei-da,ZHENGHang,ZHOULi-jiang(CAS Key Laboratory for Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230027, China)

Abstract:EPS concrete was taken as a model material for rock with defects in meso scale. Series of tests of elastic wave propagation were conducted to investigate three kinds of EPS concrete samples with EPS particle diameters of 1mm, 2mm and 3mm under different frequencies and axial loads. A so-called pulse echo overlap method (PEO) was employed to accurately determine the wave speed of samples under single frequency. Results showed that p wave speed of EPS concrete samples increases obviously with increase in loads in the initial densification stage, and then it increases slightly when sample were compressed densely; their s wave speed increases with increase in loads, but their amplitude increases much smaller than those of p wave. A relative wave speed method to compare the wave speed with the sound speed of the material under the current loads was proposed to analyze the relationships between wave speed and loads and frequencies. The relationships between wave speed and loads and frequencies were analyzed with theoretical simulation. The study results were meaningful and helpful for non-destructive checking of materials and structures with application of elastic wares.

Key words:elastic wave; EPS concrete; loading action; P wave; S wave

中图分类号:O347.4

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.011

收稿日期：2015-01-27修改稿收到日期：2015-04-09

基金项目：国家自然科学基金(11272304;11472264)资助

第一作者 徐松林 男，博士，副教授，1971年生