钢筋混凝土剪力墙非线性分析模型及损伤准则

王 宁，吕 杨(天津城建大学 土木工程学院，天津 300384)



钢筋混凝土剪力墙非线性分析模型及损伤准则

王 宁，吕 杨
(天津城建大学 土木工程学院，天津 300384)

摘要：通过LS-DYNA程序开发了一种剪力墙的宏观模型，基于此模型，提出一种适用于剪力墙的考虑首次超越破坏和能量累积破坏的双参数损伤准则．超越破坏是通过拟合各等级损伤指数与相应应变值的对数函数，累积破坏的极限耗能定义为所开发模型包络线所围成的面积，当应变阈值和累积耗能超过临界值时，可以考虑两者的耦合效应．应用所开发的剪力墙模型，数值模拟了两个剪力墙的低周反复试验，结果表明：所开发的模型能以很低的计算成本较精确地模拟剪力墙滞回关系，并且所提出的损伤准则能很好地跟踪构件损伤发展过程．

关 键 词：钢筋混凝土剪力墙；损伤准则；非线性分析模型；超越破坏；累积破坏

钢筋混凝土剪力墙的数值分析方法一直制约着结构精细化分析的发展进程，其中采用实体单元和梁单元分别模拟混凝土和钢筋的微观模型方法具有很高的模拟精度，但这种模拟方法由于计算成本过高，很难用于大型结构分析．宏观模型采用广义力和广义位移建立构件的力学相关关系，将一片剪力墙离散成一个或几个单元，这种模拟方法计算成本低，同时能保证工程上所需的计算精度，因此国内外学者通过试验研究和理论研究，提出了一系列用于模拟钢筋混凝土剪力墙的非线性动力滞回模型：如Paknahad等[1]提出的三角形单元模型能以很粗略的网格划分获得较高的精度；Mo等[2]提出一种专门用于分析墙类构件的SMM(softened membrane model)模型，并基于OpenSees软件开发了SCS (simulation of concrete structures)平台，数值分析与试验对比表明，该模型具有很高的求解精度；谢凡等[3]提出了一种能同时考虑轴向拉压变形与剪切变形相互作用，以及弯曲变形与剪切变形相互作用的新的多垂杆单元模型；基于非线性梁单元模型，朱杰江等[4]建立了一种非线性剪力墙模型．

为了分析剪力墙结构强震作用下的失效破坏过程，还需要建立剪力墙的损伤准则．目前，关于钢筋混凝土柱已经建立了很多构件层次的损伤准则[5-8]，最典型的如Park-Ang双参数模型[6]．部分准则也可以近似用于剪力墙结构的损伤分析，但由于强震作用下剪力墙损伤过程主要是水平抗力的退化过程(柱子主要是抗竖向承载力的退化过程)，并且剪力墙水平位移由剪切变形和弯曲变形等多种变形形式组成，致使剪力墙破坏点的确定方法与柱类构件有很大的差异，因此还需建立适用于剪力墙构件的损伤准则．

笔者在LS-DYNA程序[9]中开发了一种宏观的剪力墙模型，模型包络线为考虑下降段的5折线，加卸载特性通过一个3次多项式近似模拟；基于此模型提出一种适用于剪力墙构件的双参数损伤准则，准则能考虑首次超越破坏与累积破坏之间的耦合效应，适用于强震作用下剪力墙结构体系损伤过程分析．

1 损伤准则

1.1 剪力墙非线性分析模型

采用LS-DYNA程序[9]的壳单元模拟剪力墙构件应力应变关系的模型．该模型采用5条折线，分别模拟剪力墙混凝土开裂、钢筋屈服、钢筋强化、钢筋塑性流变以及强度降低等过程，并假定剪力墙不发生压溃破坏，模型包络线如图1所示．

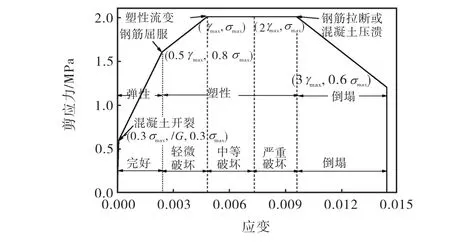
图1　RC剪力墙剪切应力-应变关系

图1中，G为混凝土剪切模量，σmax为混凝土最大应力，定义为

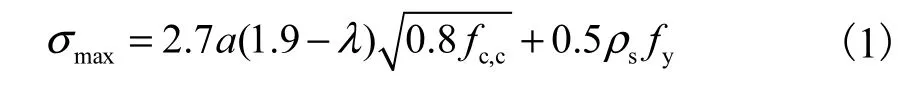
式中：λ为剪跨比；sρ为剪力墙配筋率；fc,c为受约束混凝土抗压强度；fy为钢筋屈服强度；a为考虑边缘框架对剪力墙强度提高的参数，定义为

式中：Ac、Aw分别为边缘加强构件截面积和墙体截面积．

剪力墙构件屈服后混凝土强度会发生退化，后继强度定义为

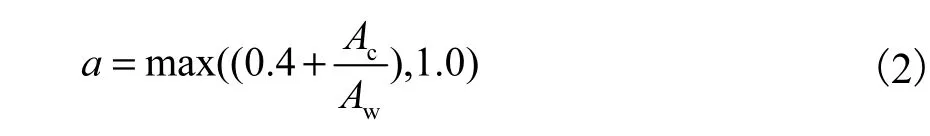
式中：χ为考虑剪力墙屈服后强度折减系数．

剪力墙极限位移由弹性弯曲、弹性剪切、塑性弯曲和塑性剪切组成，采用文献[10]的方法计算

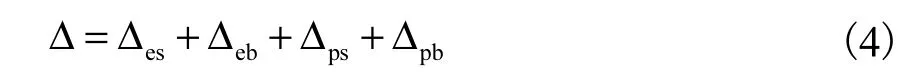
式中：Δes、Δeb、Δps和Δpb分别为弹性剪切变形、弹性弯曲变形、塑性剪切变形和塑性弯曲变形，可由下式求得：

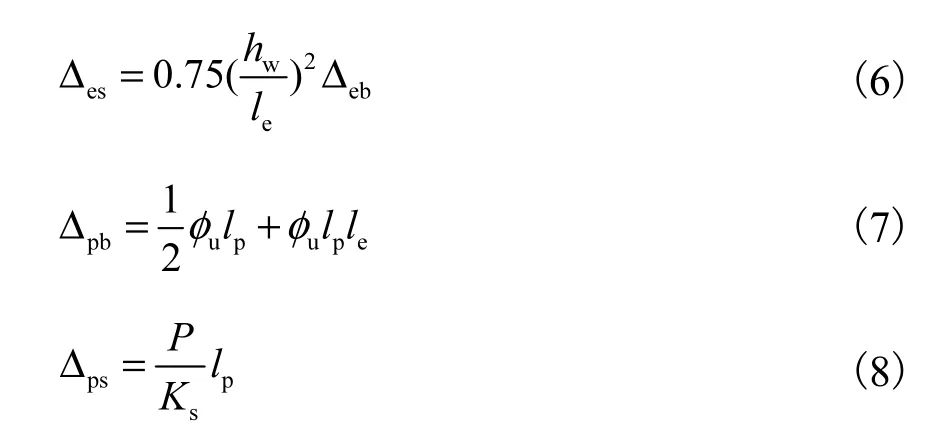
式中：le为剪力墙弹性区高度；hw为剪力墙截面高度；yϕ为剪力墙屈服曲率；lp为塑性铰长度；uφ为塑性铰区域的极限曲率；P为剪力墙峰值承载力；Ks为剪力墙塑性铰区抗剪刚度．

由式(5)-(8)求得剪力墙极限位移后，即可求得剪力墙极限应变．模型沿定义的3次多项式[9]曲线进行加卸载，如图2所示，可通过调节多项式参数控制滞回环饱满程度、加卸载刚度等．此外，所开发模型采用显示求解算法，避免了隐式求解算法中负刚度等问题，因此可以实现对剪力墙混凝土开裂、钢筋屈服和强度退化等重要性能的模拟．

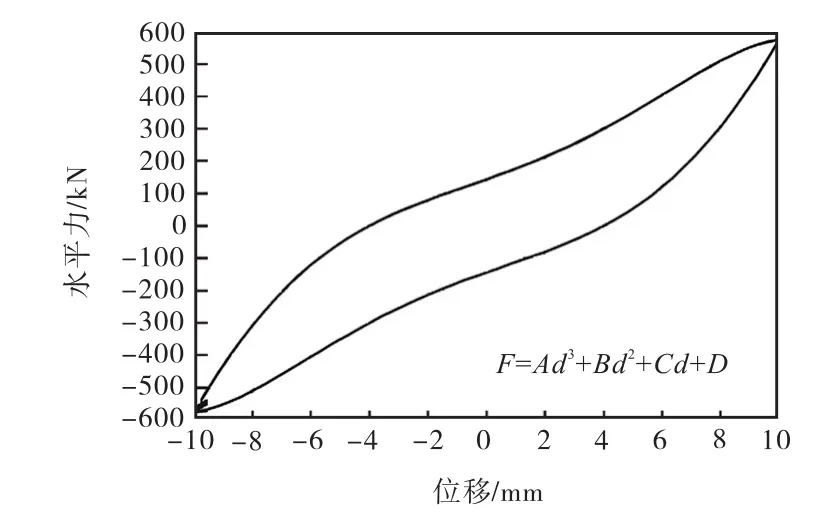
图2　模型加卸载路径

1.2 剪力墙损伤准则

地震作用下建筑结构的震害和损伤可以划分为基本完好、轻微破坏、中等破坏、严重破坏和倒塌5个等级[11]．表1和图1分别为各等级损伤对应应变值和损伤指数[12].

表1　剪力墙损伤准则[12]

已有研究表明，钢筋混凝土结构损伤破坏过程由首次超越破坏和循环累积破坏两部分组成，同时两种破坏的发展过程会相互耦合[13]，即随着循环累积破坏的发展，结构发生超越破坏的阈值会降低；反之，随着超越破坏的阈值增加，结构发生累积破坏的界限不断降低．为此，将结构损伤指数di分解成考虑首次超越破坏的dε,i和考虑循环累积破坏的dE,i，损伤指数定义为

式中：di为结构第i时间步损伤指数，根据表1所示损伤等级划分，损伤指数小于0.2时表示结构基本完好，大于0.9时表示结构发生倒塌破坏．

根据表1中剪力墙损伤状态，采用数值拟合的方法，建立剪力墙结构不同损伤等级时应变与损伤值的关系，如图3所示；同时引入参数dε和dE来考虑超越破坏和累积破坏之间的相互影响[12]，则剪力墙结构超越破坏和累积破坏可以分别定义为

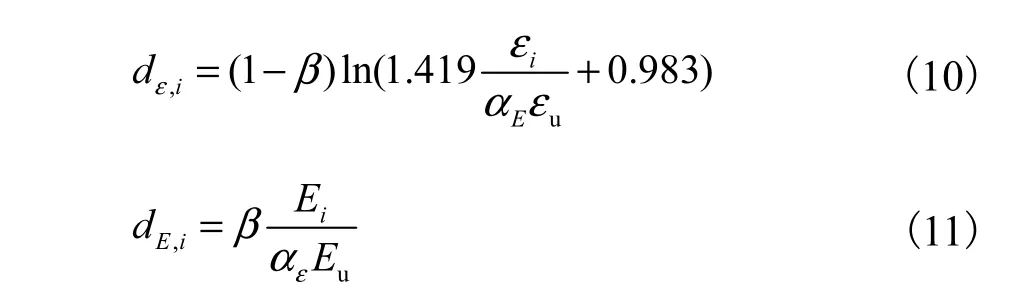
式中：β为考虑超越破坏与积累耗能对损伤贡献的权重系数；Ec、cε分别为考虑滞回耗能与损伤阈值相互影响的临界值；Ei、iε分别为第i时刻前总滞回耗能和最大应变；Eu、uε分别为极限滞回耗能和失效应变；εα、Eα分别为考虑超越破坏与累积破坏相互影响[14]的系数，定义为

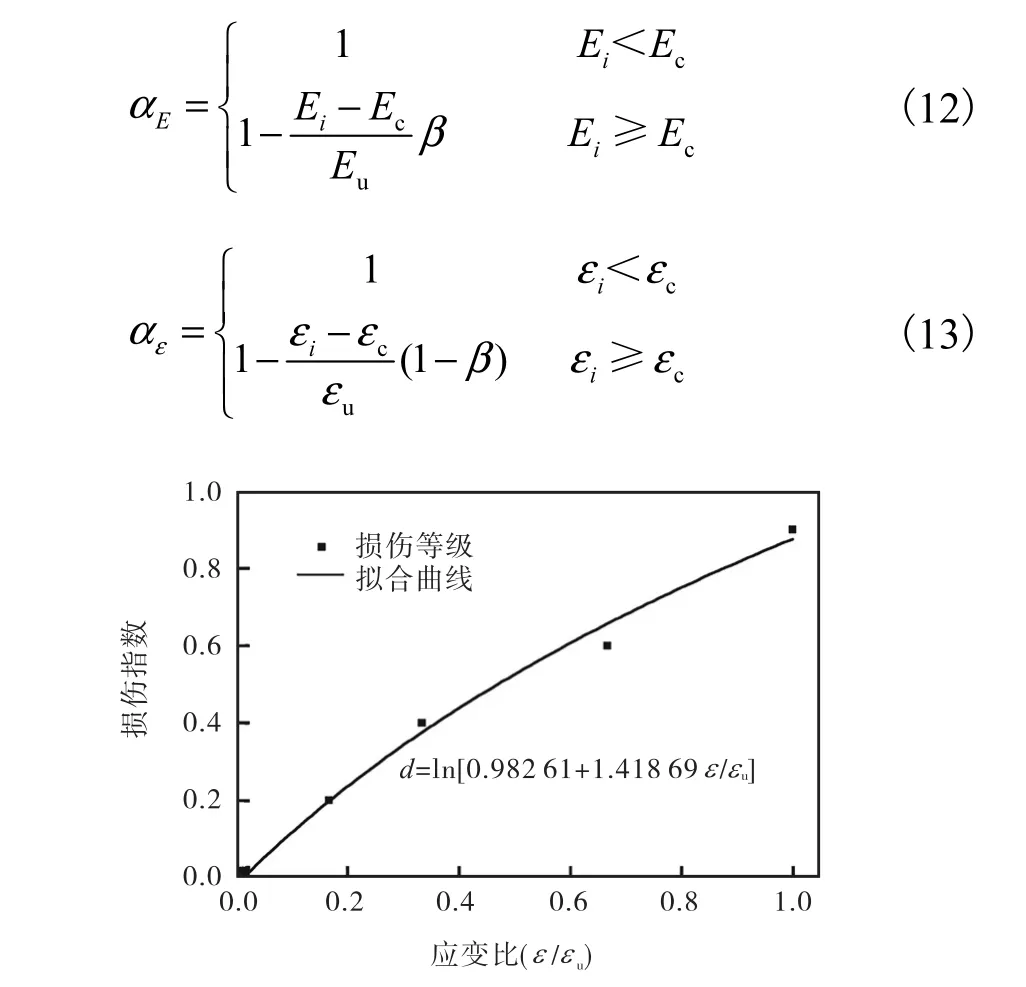
图3　损伤发展过程拟合曲线

上述损伤准则中，有β、Eu、uε、Ec和cε等5个参数需要确定．由于剪力墙和钢筋混凝土柱首次超越破坏和累积破坏过程相似，而剪力墙模型试验数据离散性很大，因此，参数β、Ec和cε采用钢筋混凝土柱的试验结果进行确定．在钢筋混凝土柱的Park-Ang损伤模型[6]中，考虑滞回耗能效应的权重系数通过下式确定

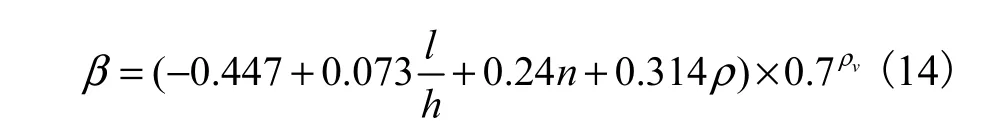
式中：l/h为剪跨比；n为柱子轴压比；ρ、vρ分别为柱子配筋率和体积配箍率．文献[6]中参数β均值大约为0.05，建议值为0.1．此外，在一些改进的Park-Ang模型中[7-8]，参数β取值在0～0.85之间，均值约为0.48．实际应用中，可以通过试验或者数值模拟的方法得到．对于普通钢筋混凝土构件，β可取0.1～0.2．Eu为剪力墙破坏时总滞回耗能，定义为剪力墙模型包络线与应变轴所围多边形的面积，如图1所示．剪力墙破坏点极限应变uε由剪力墙极限位移计算得到，参见剪力墙模型式(4)．

当Ei(或εi)大于Ec(或cε)时，考虑剪应变阈值与总滞回耗能耦合效应．钢筋混凝土柱低周疲劳试验结果表明[13]，钢筋混凝土柱不发生疲劳破坏的界限值约为最大值的25%,(μΔ＝1与μΔ＝4)，考虑到强震冲击作用下混凝土构件循环次数和地震动加速度峰值有限，取μΔ＝2.5作为疲劳破坏的上限，即Ec(cε)取Eu(uε)的40%,．

2 算例分析

采用上述剪力墙模型和损伤准则，数值模拟文献[15]中编号为HPCW-01和HPCW-02的剪力墙的低周反复试验，数值模拟滞回曲线和试验滞回曲线如图4-7所示．模型参数如表2所示，损伤准则参数如表3所示．

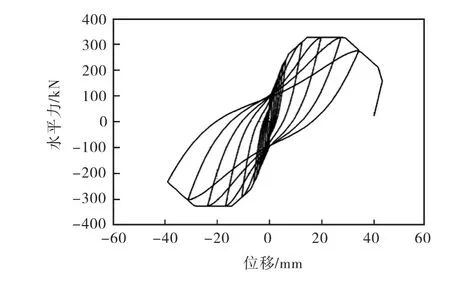
图4　剪力墙HPCW-01模拟结果

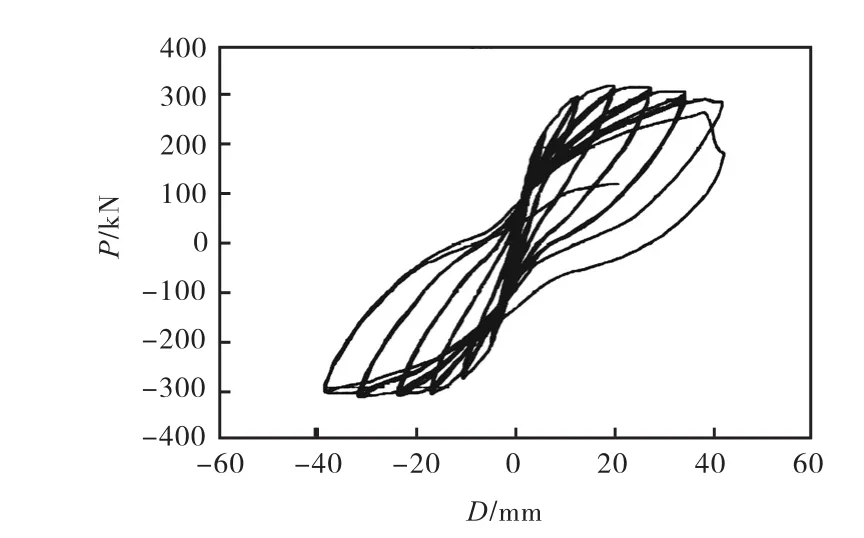
图5　剪力墙HPCW-01试验结果

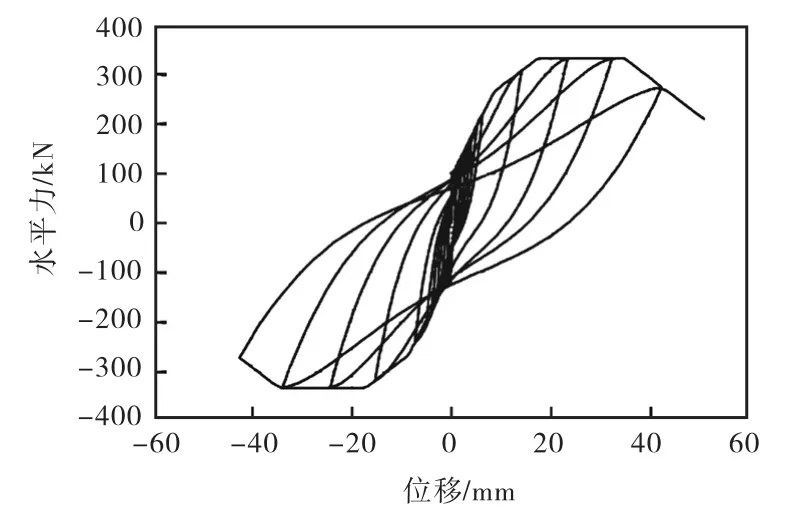
图6　剪力墙HPCW-02模拟结果

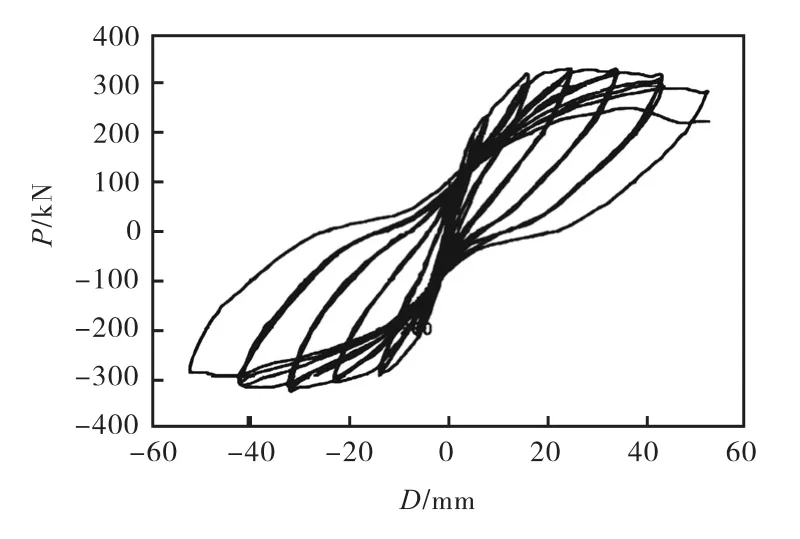
图7　剪力墙HPCW-02试验结果

从图4-7可以看出，所开发的模型能很好地模拟剪力墙反复荷载作用下的滞回过程．由图4和图6可以看出，所采用的剪力墙模型能较好跟踪剪力墙真实的力-位移关系：在加载初期，剪力墙基本处于弹性受力阶段，力-位移关系为直线；随着荷载的增大，剪力墙配置的钢筋发生屈服进入塑性流变阶段，此时剪力墙内力不随位移的增加而增大；继续加载，剪力墙内钢筋发生拉断，受压区混凝土压溃，力-位移曲线出现下降；继续加载，剪力墙逐渐破坏失效．由于模型不能模拟混凝土疲劳效应，所以数值模拟中每个荷载步只加载一个循环，并且从图5和图7可以看出，剪力墙力-位移曲线中相同位移加载的三个循环几乎重合，即剪力墙累积破坏不是很明显．

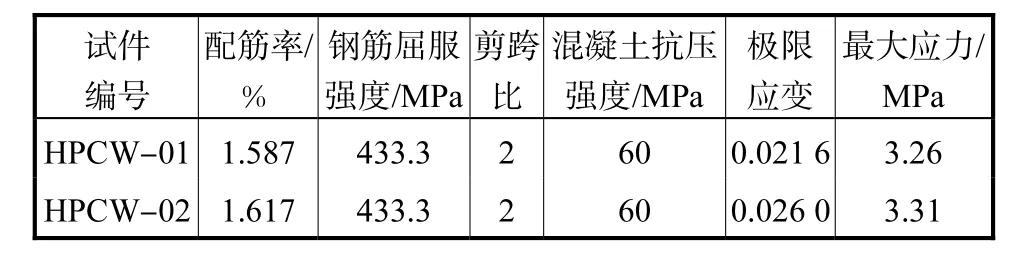
表2　模型参数

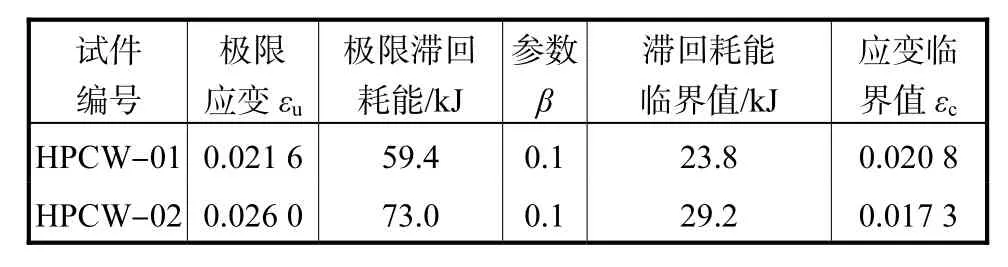
表3　损伤准则参数

应用所提出的剪力墙损伤准则计算得到两片剪力墙损伤发展过程，如图8-9所示．由图8-9可以看出：两片剪力墙损伤发展过程相似，即损伤随加载幅值的增加而逐渐增大，损伤在位移幅值变大处突变，可见本文提出的损伤准则能较好地反映拟静力试验损伤发展过程．图中实线、虚线分别表示损伤准则中考虑和不考虑首次超越破坏与累积效应的相互影响．由此可见，在应变阈值和累积耗能达到临界值之前，两种损伤准则计算得到的损伤发展曲线完全重合；当应变阈值和累积耗能超过临界值之后，考虑相互影响的损伤准则损伤发展增快．

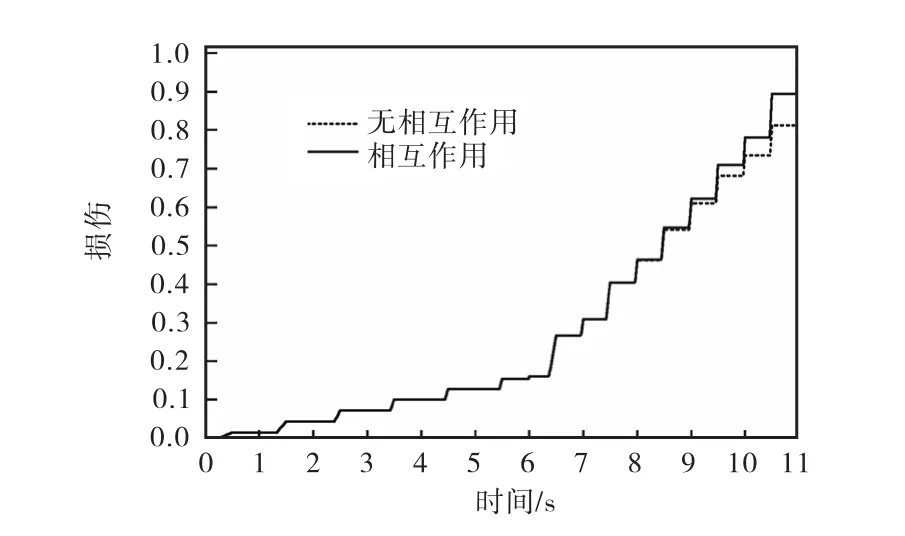
图8　剪力墙HPCW-01损伤发展过程

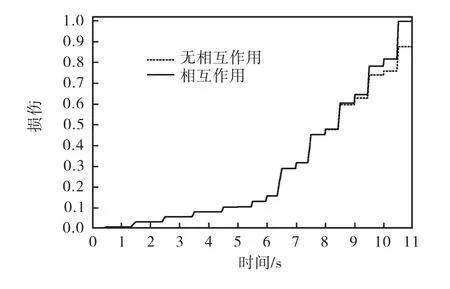
图9　剪力墙HPCW-02损伤发展过程

3 结 论

(1)所采用的剪力墙数值计算模型可以较精确地模拟剪力墙结构受拉开裂、纵筋屈服、纵筋强化、受拉钢筋塑性流变、纵筋拉断直至结构破坏混凝土压溃发展的全过程．

(2)提出的钢筋混凝土剪力墙结构的损伤准则能较好地评估结构损伤发展过程，考虑应变阈值与累积耗能之间耦合效应的损伤准则，其模拟结果更合理．

(3)所开发的钢筋混凝土剪力墙模型建模方便，计算成本低，能够较好地对剪力墙结构进行强震作用下的损伤分析．

参考文献：

［1］ PAKNAHAD M，NOORZAEI J，JAAFAR M S，et al. Analysis of shear wall structure using optimal membrane triangle element[J]. Finite Elements in Analysis and Design，2007，43(11/12)：861-869.

［2］ MO Y L，ZHONG J X，HSU T T C. Seismic simulation of RC wall-type structures [J]. Engineering Structures，2008，30(11)：3 167-3 175.

［3］ 谢 凡，沈蒲生. 一种新型剪力墙多垂直杆单元模型：原理和应用[J]. 工程力学，2010，27(9)：154-160.

［4］ 朱杰江，郑 琼，田 堃. 非线性剪力墙单元模型的改进及其应用[J]. 上海大学学报(自然科学版)，2009，15(3)：316-319.

［5］ WILLIAMS M S，SEXSMITH R G. Seismic damage indices for concrete structures：a state-of-the-art review [J]. Earthquake Spectra，1995，11(2)：319-349.

［6］ PARK Y J，ANG A H-S. Mechanistic seismic damage method for reinforced concrete[J]. Journal of Structural Engineering，1985，111(4)：722-739.

［7］ 王东升，冯启民，王国新. 考虑低周疲劳寿命的改进Park-Ang地震损伤模型[J]. 土木工程学报，2004， 37(11)：41-49.

［8］ 王宏业. Park-Ang双参数地震损伤模型的试验统计分析及改进[D]. 大连：大连海事大学，2008. 3-5.

［9］ LS-DYNA. Keyword user’s manual[M]. Livermore，California：Livermore Software Technology Corporation，2006.

［10］ 张 松，吕西林，章红梅. 钢筋混凝土剪力墙构件极限位移的计算方法及试验研究[J]. 土木工程学报，2009，42(4)：10-16.

［11］ 欧进萍，何 政，吴 斌，等. 钢筋混凝土结构的地震损伤控制设计[J]. 建筑结构学报，2000，21(1)：63-68.

［12］ 李忠献，吕 杨，徐龙河，等．强震作用下钢-混凝土结构弹塑性损伤分析[J]. 天津大学学报(自然科学与工程技术版)，2014，47(2)：102-106．

［13］ 刘伯权，白绍良，徐云中，等. 钢筋混凝土柱低周疲劳性能的试验研究[J]. 地震工程与工程振动，1998，18(4)：82-89.

［14］ 吕 杨，徐龙河，李忠献，等. 钢筋混凝土柱基于能量阈值的损伤准则[J]. 工程力学，2011，28(5)：84-89.

［15］ 田士锋. 高强混凝土剪力墙抗震试验及非线性分析[D]. 西安：西安建筑科技大学，2006：18-19.

土木工程

Nonlinear Analysis Model and Damage Criteria of Reinforced Concrete Shear Wall

WANG Ning，LÜ Yang
(School of Civil Engineering，TCU，Tianjin 300384，China)

Abstract：Based on the LS-DYNA program, a macro shear wall model is developed, in which a two-parameter shear wall damage criteria combined with the first passage damage and cumulative damage is proposed. The first passage damage is a logarithmic function fitted by the damage index and corresponding strain, and the ultimate dissipation energy of the cumulative damage is defined as the surrounded area of the envelop curve. When the threshold strain and cumulative energy exceed their critical values, the coupling effect is considered. The shear wall model is used to simulate the cyclic loading test of two shear walls, and results indicate that the model can simulate the hysteresis process precisely with low cost, and the damage criteria can track the damage process of shear wall well.

Key words：reinforced concrete shear wall；damage criteria；nonlinear analysis model；first passage damage；cumulative damage

通讯作者：吕 杨（1984—），男，讲师，博士，从事结构抗震与设计的研究．E-mail：lvyangtju@163.com

作者简介：王 宁（1989—），女，山东德州人，天津城建大学硕士生.

基金项目：国家自然科学基金(51508373)；天津市应用基础与前沿技术研究计划重点项目(15JCZDJC39900)；天津市高等学校科技发展基金计划项目(20140909)

收稿日期：2015-03-09；

修订日期：2015-07-06

中图分类号：TU398.2

文献标志码：A

文章编号：2095-719X(2016)01-0017-05