高校公共数学的教学与考核方式探讨
李志强
摘要:《高等数学》作为所有的理工科专业和经管类专业的必修课,在每学期期末的公共数学课程考察中,大部分院校都将其定为闭卷考试,成绩登记采用百分制。这种计分方法会导致试题容易时分数普遍偏高,题目偏难时,分数普遍偏低的状况,学生很难客观认识自己的学习水平。针对此情况,本文提出对高校公共数学类科目考试成绩采用常模参照方式,不设及格线。这样可以使学生及时正确认识自己的学习状况,准确定位。
关键词:高等数学;常模参照计分;正态分布
中图分类号:G642.4 文献标志码:A 文章编号:1674-9324(2016)45-0216-02
一、高等数学的基础地位
高等数学与初等数学是相对的,初等数学研究的是常值变量和匀速变化的变量之间的相互关系,而初等数学之外变量之间的关系都是高等数学研究的范围。高等数学主要是研究变量的非均匀变化,其研究的对象和方法较为繁杂,作为《高等数学》的补充,《概率论与数理统计》和《线性代数》也是研究生考试中高等数学科目的重要考试内容。高等数学主要研究的内容有极限理论、微积分(一元函数微积分和多元函数微积分)、级数理论。在几乎所有的理工科专业,经管类专业在大学一年级都会开设《高等数学》(部分专业难度要求较低,所开课程为《微积分》),曾经有调查表明,高等数学课的学习效果直接影响了后期其专业课的学习。因此,如何提高学生《高等数学》的学习效果,使学生正确认识自己《高等数学》的学习效果,是高校数学教师教学中面临的一个重要任务。
二、高等数学教学方法的建议
高等数学具有高度的逻辑性和抽象性,极限理论是整个高等数学的基础,所有的微分学概念都是所研究变量变化率的极限,而包括定积分、重积分、曲线积分、曲面积分的积分论都可认为是黎曼和式的极限,在基数的研究中,也是采用把无穷求和的问题转化为有限项求和的极限问题。所谓抽象性是指数学概念的抽象,比如极限,为了表现考察变量的变化趋势,在高等数学中引入了极限的“ε-δ”定义,该定义是大一学生学习高等数学的第一个拦路虎,如果理解不到位会对以后的高等数学学习带来很不好的影响,类似的概念还有不少。
目前,不管是研究生入学选拔性考试还是学期末的合格性考试,都非常注重“三基”的考查,“三基”即基本概念、基本方法、基本理论。在《高等数学》的学习中一定不能死记硬背,要进行以理解为基础的记忆,同时在学习中要注重总结,多整理自己的知识结构。考虑到高等数学内容的特殊性,结合笔者近几年《高等数学》的教学经验,对高等数学的教学有如下建议。
1.对学生初等数学知识的补充。由于近几年中小学教学改革成效比较突出,而相应的高等数学内容基本没什么变化。在教授《高等数学》课程时发现,很多原本在初等数学中的内容被移出初等数学教材,而相应的没有在高等数学中加以补充。这样很多知识点就成了无人教的真空状态。这就需要《高等数学》老师对这些知识点加以补充,不然一定会影响后期学习。
2.对基本概念的处理。数学概念都是比较抽象的,很难理解,而对于非数学专业的学生,学习数学主要是为了应用,因此在处理这些难以理解的数学概念时,我们可以避重就轻,把定义概念的直观含义告诉学生。比如在讲述“一元函数连续”的概念时,精确定义是从极限的角度,用函数在某一点极限值与函数值相等来定以的,对于应用要求较高的学生来说,我们可以用比较直观的语言来解释。教材里很多内容写的很详细,作为学生来说一定要抓住主要的内容,有重点的去学习。
3.对基本定理的处理。基本定理是高等数学的骨骼,整个高等数学是由几个基本定理支撑起来的。这些基本定理在数学专业的《数学分析》中称为实数完备性定理,是整个高等数学课程的精髓,虽然重要,可是太抽象,没有必要给学生讲太多。另一方面,《高等数学》中提到的极限存在定理、微积分中值定理,这一类定理也很抽象,但是都很重要,我们必须要给学生讲清。对于这些内容,我们必须给学生讲清定理的结论是什么,条件是什么,有什么几何意义。抓住这些主要的内容,就可以回避抽象的推导,又不影响定理的使用。在讲解定理的应用时一定要教学生思考问题的方法,教他们见到问题后如何找到切入点,如何把已知条件和要证明的结论建立起联系,培养学生独立思考问题、分析问题和解决问题,而不是单纯地告诉他们结论是什么。
4.对基本方法的处理。《高等数学》中的基本方法不多,但是都很重要。比如在导数的计算中,涉及的方法主要有,基本定义法,四则运算法,复合函数求导数,反函数求导数等基本方法,对于这些基本技能,要求学生有针对性的学习,万变不离其宗,掌握了这些基本的技能就可以以不变应万变,解决各种不同的求导问题,这些求导的方法在后期二元函数的偏导计算中也有很强的借鉴作用。再比如在不定积分的分部积分公式中,如何选择适当的函数u,v是做题的关键,只有选择正确了函数,才能事半功倍,最终我们总结出“指三幂对反,谁在后面谁为u”的总结。另一方面,还需要针对目前学生普遍眼高手低的特点,要求学生必须动手练习。
三、公共数学考核方式改革
目前《高等数学》的考核方式主要是闭卷考试,成绩登记方式主要是用百分制,即卷面成绩与平时成绩加权后就是课程的成绩,这种计分方法会导致试题容易时分数普遍偏高、题目偏难时分数普遍偏低的状况,学生很难客观认识自己的学习水平。为此我们提出用常模参照计分的方法来登记《高等数学》公共课的分数,不涉及格线,各个专业可以根据本专业需求自己定及格线。
常模参照计分的方法原理主要是借用目前四、六级的成绩发布方式。首先在所有开课学生中选出具有代表性的常模群体,用Mean表示常模群体的平均分,用SD表示常模标准差,考生的原始成绩X经过常模转换后分数即常模转换分TotSco计算公式为:
TotSco=■×7+80
上述公式的原理是概率论中,大量的学生的同一门课程考核成绩是服从正态分布的,通过选择具有代表性的常模群体,用所选的常模群体的平均分和标准差作为某次考试全体学生成绩的平均值和标准差,用这种方法的好处就是能反映出学生的真实学习效果。
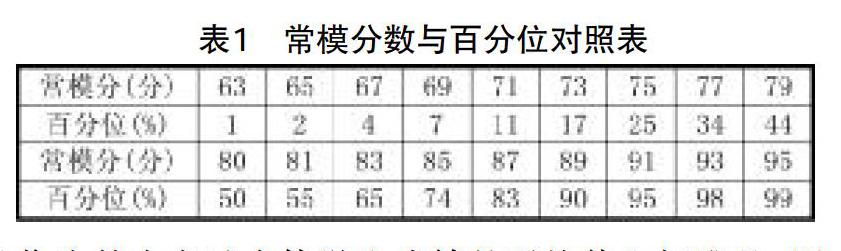
例:比如考生《高等数学》的报道总分是75分,从表1可以查出该考生在常模学生中的相应百分位是25%,表示这名考生的《高等数学》成绩优于常模群体中25%的人,但劣于75%的人。
常模参考在《高等数学》课程考核中可以使用的原因主要有三点:(1)学生的学习成绩是服从正态分布的;(2)《高等数学》的受教面比较广,基本所有本科新生都要开设这门课,因此,就有选择参照常模群体的客观条件;(3)学生的成绩几乎分布在[60,100]之间,便于各个专业对数学的不同要求选择合适的分数作为及格线。
当然该方法也有一定的缺点,不适合学生群体较小的课程,比如专业课,往往有几十名学生,就无法选择出具有代表性的超模群体,从而无法对学生的成绩进行正态化。
四、总结
本文提到的《高等数学》的教学方法和考核方式的建议也适用于其他的公共数学课,比如线性代数等。本文提到的常模积分方式主要是受到目前全国大学生英语四、六级考试的积分模式的启发,运用概率论中正态分布的特点将学生的原始分数转化为常模分数,一方面能让学生正视自己的分数,正确认识自己的学习效果,另一方面也能方便各个专业对数学提出不同的要求。
参考文献:
[1]同济大学数学系.高等数学(上下册)[M].北京:高等教育出版社 第七版,2014.
[2]盛骤,谢式千.潘承毅.概率论与数理统计[M].北京:高等教育出版社 第四版,2008.
[3]同济大学数学系.线性代数[M].北京:高等教育出版社 第五版,2007.
[4]华东师范大学数学系.数学分析(上下册)[M].北京:高等教育出版社 第四版,2010.

