初中数学应用题审题技巧略谈

张乃芬

一般来说，解应用题的思维过程大致如下：就一道具体的应用题而言，是属于常见的简单题，还是常见的较难题，或不常见的题，对于不同的学生来说不一定是相同的。所以，在课堂教学中，对于一道应用题来说，到底是直接式，还是先画示意图、列表格、再列式，或要联想实际模型再列式，要视学生具体情况而定。

要提高学生解应用题的能力，除了在广度上适当增加一些题目的类型，在深度上适当增加一些题目的难度外，更重要的是：

（1）仔细读题，抓关键词句；

（2）抽象审视，不同问题类型化；

（3）逆向思维，执果索因；

（4）数形结合、语言互译，辩明数学关系。通过以上四个方面的教学，可以沟通数学应用与实际模型之间的联系，使学生从本质上去认识数学应用题，把应用题的教学，从“知识型”、“问题型”的层面上升到“能力型”的层面。

一、仔细读题，抓关键词

数学应用题不象一般的纯数学意义的习题那样简短，而需要较多的文字表述，那么，审题时，就要“去粗取精”，把具有代表一定意义或数学关系的词句挑选出来，这是审题的第一步，是建立数学模型的基础。

例1 把100元按照1年定期储蓄存入银行，如果到期可以得到本息111.3元，那么这种储蓄的年息是存款的百分之几？

题中的关键词及数据：

（1）作为条件：100元（本金），1年定期，到期本息111.3元；

（2）作为所求：实际上是利率。

题中的关键句：如果到期可以得到本息111.3元。

为什么说这一句是关键句？这是因为这句包含的关系多，把它搞清楚了，这个题目也就易于解决。

二、抽象审视，不同问题类型化

实际问题各种各样，千差万别，因此，数学应用问题就千姿百态，各不相同，但只要认真审视，从数学的意义上进行概括、抽象，那么，应用问题就将分门别类，以有限的数学形式或数学模型表现出来。比如，形成问题、利率问题、工作效率问题、生产率问题，在生活生产实际中均自成体系，但其数学模型都是数学中的“三量公式”AB=C。要善于用数学抽象的眼光审视，这样才能拨去问题的“外衣”，透过表层看问题的本质，建立恰当的数学模型也就不难了。

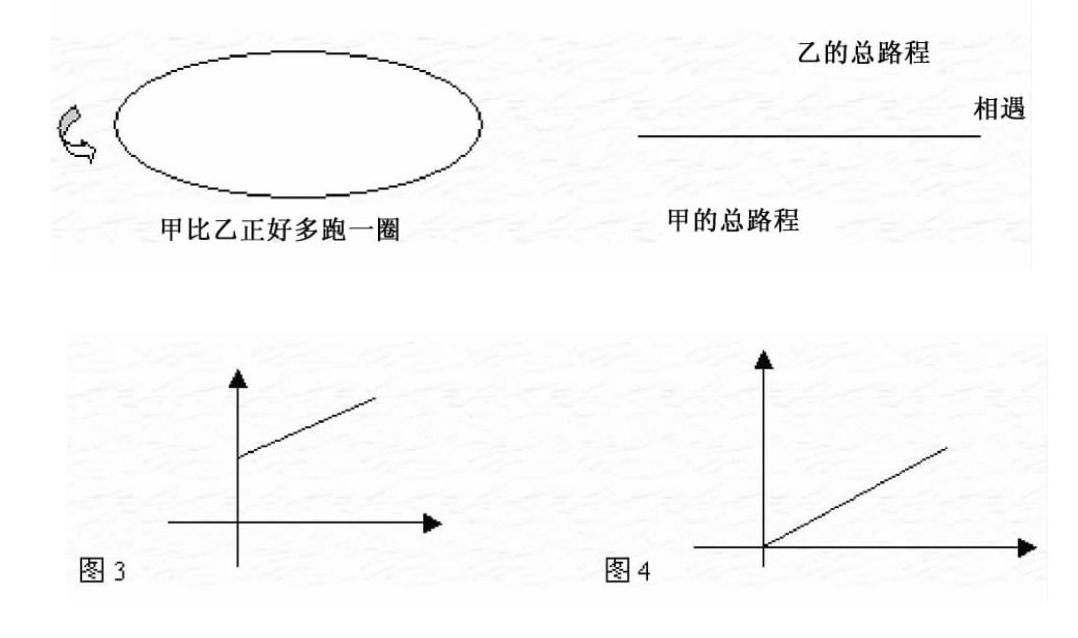
例2 运动场的跑道一圈长400米。甲练习骑自行车，平均每分骑490米；乙练习跑步，平均每分跑250米。两人从同一处同时出发，经过多少时间首次相遇？（初中《代数》第一册（上）P.243）

这题的环形（跑道）“割开”拉直，就变成下面的“同类”题。

例3 A、B两地相距400米。甲乙两人同时同向分别由A、B两地出发。甲骑车，平均每分490米；乙跑步，平均每分250米，经过多少时间两人相遇？

三、逆向思维，执果索因

“走过”迷宫的人都有这样的体验，往往正行容易碰壁，反行倒觉得较为顺畅，再做标志，正达到目标。解题也一样，对一些正面难以入手的问题，不妨由结论向条件方向探索分析，打同各种关碍，最后由条件出发，写出解题过程。

如例3，如果两人所用的时间知道，设为X分，那么，因为两人的速度已知，就可以知道两人各自的行程，分别为490X、250X。两人的行程之差实际上就是A、B两地的距离400米。这样一来逆行完毕，可列出方程：490X—250X=400

例4 某校组织350名师生去参观黑河引水工程建设，如果租用甲种客车若干辆刚好坐满；如果租用乙种客车则可少租1辆，且空余10个坐位。已知甲种客车比乙种客车少10个座位，问甲、乙两车各多少座位？

四、数形结合、语言互译，辩明数学关系

一般的应用题都是以文字说明加一定数据组合而成的，这时候首先要抓住关键词句，把它们译成数学图形语言或符号语言，这时候对打开思路是很有必要的。另一方面，有写应用题是以图表的形式出现，这时候，就要认真观察分析，把图表语言译成数学符号语言或一般文字表述，以加强对问题的透视。各种语言的互译，就是为辩明数学关系服务的。

例5 为了发展电信事业，方便用户，电信公司对移动电话采用不同的收费方式，其中所使用的便民卡与如意卡在某市范围内每月（30天）的通话时间X分与通话费Y（元）的关系如图2、图3所示。

（1）求出通话费Y1、Y2与通话时间X分之间的函数关系式；

（2）请帮用户计算，在一个月使用哪一种卡便宜？

本题的主要问题是写出函数关系式，但有关信息只以图形的方式呈现，那就必须读懂图形，将其转化为文字或数学符号语言。

审题策略既有其共性，也因人随题的不同而表现出思维策略、方法技巧的多样性，解题时应灵活运用。