基于分治策略的贝叶斯网学习方法及在图像分割中的应用

段宏英　姜威　于帅

[摘要]贝叶斯网将概率论和图论相结合，是一种描述随机变量间依赖关系，并能紧凑高效的表示联合概率分布的概率图模型，近年来已成为人工智能理论中处理不确定性问题的重要工具，面向大数据的贝叶斯网学习方法一个重要问题。论文给出了基于分治算法的高维贝叶斯网学习新思路，并给出了其在图像分割领域中的应用策略。

[关键词]贝叶斯网；图像分割；分治算法

1 引言

随着大数据时代的到来，人类所获得的数据往往存在海量、高维等特点。贝叶斯网学习是NP问题，其计算量随贝叶斯网变量数目的增加呈指数级增长。虽然面向常规数据的贝叶斯网学习技术已取得很大进展，但当用于学习的数据维度很高、即目标贝叶斯网的变量数目庞大时，贝叶斯网学习算法的计算复杂度很高，学习十分困难，如何从高维数据中高效的学习贝叶斯网是一个挑战性问题。

为此，本文提出针对高维数据的复杂贝叶斯网的高效学习新思路，并给出将研究结果应用于图像分割领域的实施方案。

2 基于分治策略的高维贝叶斯网学习思路

基于“分而治之”的思想，研究对高维数据的变量进行高效分组的新方法，使每组内部的变量有着极强的依赖关系，而各个组之间的关联关系较弱。进而可独立分别学习各组结点对应的单元贝叶斯网，最后将学得的各单元贝叶斯网合并以得到最终贝叶斯网。

首先使用已有研究成果从数据中求得贝叶斯网中每个变量的可能父结点集合，并对每个变量可能的父结点排序（比如基于条件互信息的值排序）；然后基于上述结果，借鉴前人提出的“父结点关系图”的思想，生成一个有向有环的草图，将可能存在父子结点关系结点对都用有向边连接，该图并不是真正的贝叶斯网。只是最大程度反映贝叶斯网结点间可能的父子关系，可能存在众多环结构，X可能是Y的父结点、Y也可能是X的父结点。

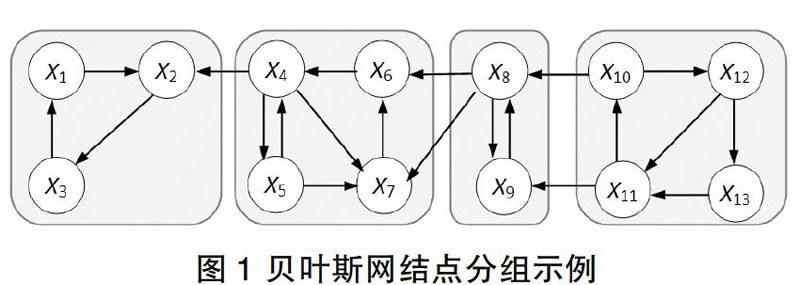
按下面原则对结点进行分组：如果一个结点集U中的结点可能是另一结点集V中结点的祖先，但V中结点并不可能是U中结点的祖先，即这两个集合间不存在环（各自集合内可以存在环），则将这两个结点集分进不同的组。一个例子如图1所示。图1中将结点分为4组，每组结点间不存在环，组内存在环。这意味着每组内部的结点有着极强的依赖关系，而各个组之间的关联关系较弱。

基于“分而治之”的思想，独立处理每组结点集合，可大幅提高贝叶斯网学习效率。研究处理组间连接的方法，即每组结点对应的小贝叶斯网学完之后如何合并成最终的贝叶斯网。例如对于图1，X₄可能是X₂的父结点，如果只是单独学习结点集（X₁，X₂，X₃）对应的贝叶斯网，则学习完之后就较难和其他组结点集对应的贝叶斯网合并。我们试采用如下策略：第一组结点结点集（X₁，X₂，X₃）的学习考虑将X₄作为X₂的可能父结点之一，但不学习X的父结点，X₄的父结点放在第二组中学习。即针对每组结点集的学习过程中，也考虑在其他组中的可能父结点。这样，最终将图1分为下面的4组结点集，可分别独立学习这4组结点对应的贝叶斯网，如图2所示。

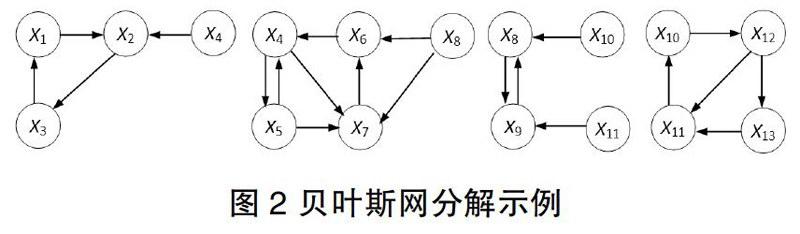
独立学习按上述策略得到的各组结点对应的贝叶斯网，一共分为n组，则学得n个贝叶斯网，我们称之为单元贝叶斯网，最后将这n个单元贝叶斯网的重复结点合并，即可得到最终的贝叶斯网。研究控制分组数目的方法，如当上图中有向边很稠密时，利用结点与其父结点的互信息，对边进行精简，以增加分组数目。

3 基于贝叶斯网的高效图像分割策略

针对当前图像分割基于多分辨率算法中低分辨率图像的优点全局性强利用不够充分，可使用贝叶斯网在不同分辨率之间信息传递来消除或减少图像分割中由于受到噪点等而产生的过分割现象。针对多分辨率图像辅助决策方法存在各级分辨率的决策结果效果不一的问题，可使用信息融合算法合理总和这些结果进行决策，使最终边界认定更准确。整体流程如图3所示。

4 结束语

针对高维复杂数据下贝叶斯网学习问题，本文给出了基于分治算法的高维贝叶斯网学习新思路，并给出了其在图像分割领域中的应用策略，对拓展贝叶斯网的理论与应用具有重要意义。