捕捉与巧用数学课堂的生成性教学资源
黄红莲
[摘 要]
新课程理念下的数学课堂教学是一个动态的过程,具有灵活的生成性和不可预测性。教师应在数学课堂教学中及时捕捉和巧妙利用生成性教学资源,激发学生探究问题欲望,提高课堂教学效率。
[关键词]
教学资源;动态;有效性
数学新课程标准指出,积极开发和利用课程资源是数学课程实施的重要组成部分。数学课堂教学是一个动态的、不断发展的过程,具有灵活的生成性和不可预测性。随着新课程标准的实施,由学生动态生成的教学资源已引起教师更多的注意。如果教师能在数学课堂教学中巧妙地捕捉和利用生成性教学资源,将会促进教师和学生的共同发展。如何在数学课堂教学中巧妙地利用生成性教学资源非常值得研究。
一、利用教材,诱导生成
评价一堂课的效果,外行看热闹,内行看门道。要把数学课堂中“闹”和“道”做好,就必须“激活”教材,让枯燥课本知识恢复到“鲜活状态”,在课堂教学中凸显知识的活性。因此,教师不仅要充分了解学生的认知基础、思维特点以及心理状态,还需对教材提供的教学资源认真领悟,深入挖掘,创造性地处理和使用。同时引领学生主动参与并体验探索知识的历程,巧妙处理预设外的生成性资源。
例如:[案例]一位教师教学“同底数幂的除法”时,引入计算:①35÷33=( ),②315÷35=( ),③a6÷a3=( )……学生根据自己的计算得出了结果。师:你是怎样计算的?生1:我是把两个乘方算出来再相除。生2:我是利用乘方的的定义,写成分式形式,分子五个3相乘,分母三个3相乘,再约分得到的。这时教师发现还有一名学生在举手,就让她回答。生:由乘法和除法互为逆运算,想到谁和33相乘得35呢,由曾经学过的同底数幂相乘可得出是3的平方。利用同底数幂相乘的性质,导出了本节课同底数幂相除的性质。
本案例中,教师创设了宽松的学习情境,让学生积极主动的投入到探索知识的过程中,由学生提供的已学知识出发,引出本节课知识。这个问题的生长点就在于个别学生对同底数幂相乘的性质进行了联想和逆用,进而在“同底数幂相除”之处也出现了新的生成,跳出了一般思考的局限,利于学生将知识纳入自己的知识网络,从而系统掌握。根据教材的内容出发,充分挖掘教材内涵,指导学生经历学习过程,不仅对知识的建构有很大帮助,而且有助于激活学生的潜能,把握数学知识的本质。因此,深入研究教材是动态生成的起点。
二、“意外资源”,引导迁移
在动态生成的课堂上,教师在明确学生是数学学习的主人,同时注意学生的想法。学生的一些不同寻常的想法,往往蕴涵创新的思维、智慧的火花。在教学中,经常会发生一些被认为是不利于本节课教学事件,因此,教师不予理睬,其实,这样的课堂教学不利于学生的个性发展。教师应巧妙地将其转化为能为课堂教学服务的教学资源,让课堂充满活力。
案例:《12.2全等三角形》教学片段(新人教版八上)
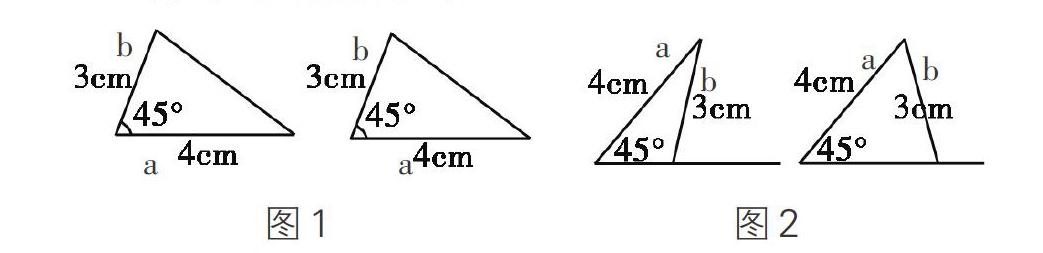
1.让学生画一个三角形,使它满足两条边长a、b分别为4cm和3cm,且它们的夹角为45°。画完后用剪刀剪下来,和其他同学剪的三角形比较,看看是否能够重合。
2.让学生画一个三角形,使它满足两条边长a、b分别为4cm和3cm,且其中一条边的对角是45°。
满足条件的三角形出现了两种形状完全不同的三角形(如图1)。
1)当45°为a,b两边的夹角时,所画三角形是唯一的;即是全等三角形。
结论1:两边和它们的夹角对应相等的两个三角形全等。(边角边公理)
简写成“边角边”或“SAS”
2)当45°为a,b两边其中一边对角时,所画三角形是不唯一的(如图2);
结论2:两边及其一边所对的角相等,两个三角形不一定全等。
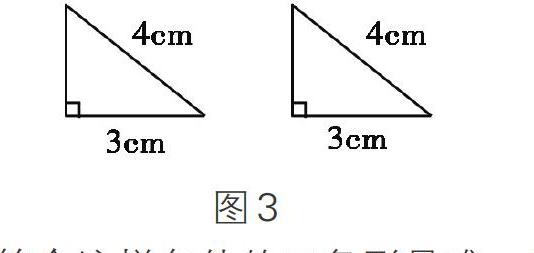
生:以3cm、4cm为三角形的两边,让长度为4cm的边所对的角为90°,情况发现也只能画一个三角形(如图3),符合这样的条件能判定两三角形全等吗?
结论3:符合这样条件的三角形是唯一的,也就是全等的,这个是特例。(在今后的学习中会揭示这一特殊的类型)
这时一学生说,我以3cm、4cm为三角形的两边,让长度为4cm的边所对的角为100°。符合这样条件的三角形是唯一的,也应该是全等的。
结论4:符合这样条件的三角形是唯一的,也就是全等的。但应用条件较多不作为定理应用。
学生在学习中会出现一些与众不同的想法,这些想法对于新知识学习的帮助,学生本身可能并不知情,但教师一定要抓住机会,机智对学生生成的这些资源加以注意和利用,自然地运用到教学之中。在上述边角边公理探究过程中,我们不难看出,当学生的回答远离或背离我们的预设的时候。教师可以利用生成的“转折”资源,进行知识的迁移,既达到预设的目标,又能扣紧“生成点”促进学生的发展,为后续学习做铺垫。
三、“单一”资源,追问补充
在课堂教学过程中,面对学生在学习过程中生成的单一信息资源,教师要有丰富的课堂教学经验,敏锐的观察力和灵活的教学机智。实时地将学生在学习过程中生成的单一信息资源,转化为积极的、丰富的生成性课堂教学资源。
由上个案例中,我们不仅得出边角边公理,而且还可得出斜边、直角边公理;还知道“边边角”中若角为钝角时结论也成立。若学生没有发现结论3和结论4,则可引导他们“角”为直角和钝角时情况。为以后的学习做铺垫。面对学生中出现的意外生成性资源,充分相信他们,为他们创设宽松的学习环境和自主探索的空间,生成新的更有价值的见解。根据课堂生成的合理调整,看似浪费了课堂宝贵的时间,但其中蕴涵的却是数学教学中化归思想的灵活运用,唤起的是学生对数学学习的兴趣和灵感。带着知识走向学生,不过是“授人以鱼”,带着学生走向知识,才是“授人以渔”。数学课堂教学效率的高低不取决于教师预设效果的掌握情况,而取决于学生实际获得知识。在课堂教学中,只有引导更多的学生主动参与数学活动,才能掌握数学基础知识、基本技能和数学思想方法,才能真正提高学生的数学素养。
四、错误资源,回归“正轨”
心理学家盖耶说得好:“谁不考虑尝试错误,不允许学生犯错误,就将错过最富有成效的学习时刻。”在教学过程中,对于学生出现的错误,有的时候我们只看到的是消极的一面,千方百计避免学生出错。其实,课堂中学生出现的错误,正是他们真实的思维方式的表现。学生的错误往往是正确的先导,学生思维中所谓的“错误”,正是思维过程中的闪光之处,它反映了学生的思维能力,真实想法,它其中也包含着合理的成分。因此,老师要抓住这个“错点”把学生引向预设点。在平时教学中,要允许学生出错,让学生在错中悟理,在错误解法的解法中,挖掘出隐藏的创新因素。因此,教师不能轻易给学生的错误回答判“死刑”,而将错误作为课堂教学的一部分巧妙地服务于数学教学,使错误成为促进学生发展的资源。从而让学生体验到“不经历风雨,怎么见彩虹”的诗意哲理。
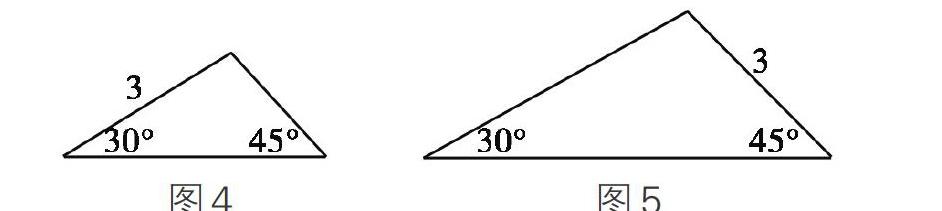
案例:《12.2.3全等三角形》教学片段(新人教版八上)在得出两角和它们的夹边对应相等的两个三角形全等即“ASA”后,老师提出:两个角和其中一个角的对边对应相等的两个三角形会全等吗?生不假思索齐答会。师追问理由?原以为学生把它转化为刚学过的“ASA”就可以了,可习惯动手操作的他们,同桌一约好具体的边、角数据,就开始画图、剪拼验证起来了,老师正想引导学生往预设思路“不用实验的方法你能证明这个命题吗?”这时有个学生在下面喊了起来:“老师,我和同桌的两个三角形不全等”。全班同学开始议论了,究竟是怎么回事,老师一看明白了其中的原因,这是一个非常好的错点资源,何不充分利用呢?老师随即把他俩所剪的三角形展示出来:(如下图4、5)
学生们很快就找出了其中的原因,并深刻理解了“对应”的含义。在学生刚接触用“SSS”、“SAS”、“ASA”判定三角形全等时,我一直找不到合适的机会解释“对应”两个字,而学生也一直不甚理解,今天这次意外生成的亮点资源的及时捕捉,却使师生困绕很久的问题得以圆满解决。《数学课程标准》指出“有效的数学学习不能单纯地依赖模仿与记忆,动手实践、自主探索与合作交流是学生学习数学的重要方式。”通过这个亮点资源的及时捕捉,使我更深刻地理解了这句话。
总之,课堂资源不仅指教学资源、教学环境、教学技术等,因而我们应重视课堂教学中突发的每一件事,善加捕捉与利用。让“动态生成”给师生带来意外的感觉,而这种意外往往会给学生带来探究的冲动,课堂的活力经常在这样的情景中迸发出来,所以我们应从关注生命的高度,用变化的、动态的、生成的而非静止的僵化的观点来看待课堂教学,充分有效地利用课堂中的动态生成资源,让课堂焕发生命活力。
[参 考 文 献]
[1]韩国梁.让数学课堂活起来——数学课堂局部探究的尝试[J].中学数学教学参考(上旬),2012(5).
[2]王坦.新课程与学习方式的变革[M].北京:北京师范大学出版社,2002.
(责任编辑:张华伟)

