中职数学课学生参与意识和自主学习能力的培养
常鑫海
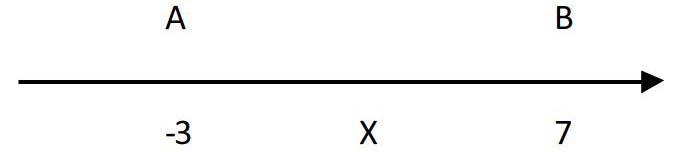


摘 要:中职生在数学课学习中的参与意识和自主学习能力普遍欠缺,教师应为学生提供广阔的天地,帮助、引导他们通过探索获得知识、技能,培养他们的创造力,激发他们的潜能。
关键词:中职数学;参与意识 ;自主学习能力
中图分类号:G71 文献标识码:A 文章编号:1673-9132(2016)23-0192-02
DOI:10.16657/j.cnki.issn1673-9132.2016.23.122
一、教师要做好多种角色的扮演者
1.教师是导演,学生是那些拥有个性和创造力的演员。教师应根据课堂信息不断变换方式,不仅要适应学生的学,而且还要指导不同层次的学生去学、去探究。如讲解:
例1:已知:|x+7|+|x-3|=10,求x的取值范围。
此题学生一般都用去掉绝对值符号的办法来解决,但为了开阔学生的思路,确立数形结合的思想,我们可用绝对值的几何意义来解,这样解题也更简便。
解:设A、B、X分别是数轴上表示-7、3和X的点,则X与A、B两点之间的距离之和是10,由图可知当X在A、B两点之间的任一一个位置(包括A、B)时,线段XA与XB长的和总是10,而在其他范围之外则大于10。故-7≤x≤3。
2.教师是学生学习过程的引路人、评论员、结果的仲裁人。教师要对学生的学习活动给予及时的评价,抓住学生奇妙的思想火花,大加赞赏。
例2:已知函数y=mx2+(m-1)x+m的图像与x轴有两个不同的交点,求m的取值范围。
极大部分学生都会直接运用抛物线与x轴的交点个数和根的判别式来求解,此时教师提出来这样解答是否正确,而后再剖析:因为函数的图像与x轴有两个不同的交点,所以此函数必定是二次函数。剖析后学生很快就发现题目中的隐含条件m≠0。只有当m≠0时,才有判别式的存在。所以本题解答的错误是双重的。如何求解呢?此时学生便兴味盎然地开始重新审题。
此时我们采取的教学对策是:在二次函数的教学中,首先要向学生强调二次函数的定义有两部分构成:①表达式为y=ax2+bx+c;②二次项系数a≠0。其次还要告诉学生在解形如y=ax2+bx+c的函数问题时,一定要分a=0和a≠0两种情况来考虑,当a=0且b≠0时此函数为一次函数,当a≠0时此函数为二次函数。
二、要提高课堂教学中学生的参与程度
现行中职教材旨在培养学生的创新精神、实践能力、终身学习的能力和适应社会生活的能力。新教材的特点之一是有利于学生的阅读与自学,如学习了两角和与差的正弦、余弦、正切的公式之后,对二倍角的正弦、余弦、正切的公式就要求学生发现规律,总结得到结论。如:
例3:已知圆的方程是x2+y2=r2,求经过圆上一点(x0,y0)的切线方程。
此题用斜率和点斜式方程解答,但没有注意到斜率不存在的情形,解答不完全,此时若提出若M在x轴或在y轴上,上述解答是否完整,学生就会思考、探索发现问题。若M在x轴上,切线斜率为0;若M在y轴上,切线斜率k不存在, OM的斜率不存在,上述解答就不合理,如何解决此问题,就要分类,即在直线斜率存在、不存在的两种情况下解直线方程,学生就能给出正确的解答。
设P(x,y)是切线上异于M的任一点,OM⊥PM,则|OM|2+|PM|2=|OP|2,即x02+y02 +(x-x0)2+(y-y0)2= x2+y2,
三、要培养学生主动学习数学的意识
1.兴趣是学习的动力。学生对学习有积极的兴趣时,他们的思维就会活跃,参与活动的欲望就会被激发出来,表现欲就会大大增强。如讲直角三角形与勾股定理时,可穿插“毕达格拉斯的轶事”,以引导学生的兴趣,加深他们对所学知识与思想方法的理解。
2.创设良好的教学情境,营造和谐的课堂氛围。教授在教学中可设置“漏洞”,为学生创设知“漏洞”、改“漏洞”的教学情境,让学生细心观察,养成勤于思考的习惯,让学生在落入和走出误区的过程中,培养学习数学的兴趣。
例4:试判断函数f(x)=奇偶性。
有学生计算f(-x)后得出f(-x)≠ f(x) ,f(-x)≠ -f(x)得出f(x)为非奇非偶函数,又有学生认为,先判断分母 -3≠0得x≠0或x≠6,定义域关于原点不对称, f(x)为非奇非偶函数,事实上以上结论是错误的,对此好些学生感到困惑不解。为了解开学生的疑团,让学生在定义域和解析式上再做深入的探究,结果会发现求定义域时学生没有考虑分子,正确的定义域应为{x|-2≤x≤2,且x≠0}是关于原点对称的,化简得f(x)=,所以f(x)是奇函数。
教育的本质和功能决定了教育是通过教育工作者和受教育者共同实现的文化传承。在教学过程中,学生是学习的主体,我们要采用多种方式使学生参与到教学中来,主动探究知识的奥秘。
参考文献:
[1] 魏秀果.中职数学课程改革专业化策略论[J].数学学习与研究,2011(15).
[2] 李求来.《初中数学课堂教学研究》.湖南师范大学出版社,2005.
[3] 陈猛.中职数学教学中培养学生自主学习能力研究[D]. 西北师范大学,2004.
[4] 夏章平. 中职数学教学中学生自主学习能力的培养[J].中国信息,2014(9).
[5] 胡菊红.新课程下中职学生数学多元化的自主学习方式探究[J]. 新课程,2015(5).
[6] 郑玉琳. 提升中职生数学自主学习能力的教学研究[D].湖南师范大学,2010.
[责任编辑 吴海婷]

