浅谈思维导图在《圆的一般方程》教学中的应用

冯柱

摘 要：思维导图（Mind Map）是英国著名学者东尼·博赞（Tony Buzan ）在19世纪70年代初期创立的一种新型笔记方法，它以放射性思考为基础，是一个简单、高效、放射性、形象化的思维工具，能够全面调动左脑的逻辑、顺序、条例、文字、数字以及右脑的图像、想象、颜色、空间、整体思维，其在数学教学中，能够很清晰的构建数学知识与数学思想间的联系，对培养学生学习数学的兴趣，调动学生学习的积极性，保持学生学习的主动性有着很深远的意义。

关键词：思维导图 数学课堂

中图分类号：G633.6 文献标识码：C 文章编号：1672-1578（2016）09-0103-02

1 思维导图及其特点

思维导图运用图文并重的技巧，把各级主题的关系用相互隶属与相关的层级图表现出来，把主题关键词与图像、颜色等建立记忆链接，充分运用左右脑的机能，利用记忆、阅读、思维的规律，协助人们在科学与艺术、逻辑与想象之间平衡发展，从而开启人类大脑的无限潜能。同时，思维导图还是一种将放射性思维具体化的方法，人类从一出生即开始累积这些庞大而复杂的数据库，大脑惊人的储存能力使我们累积了大量的资料，经由思维导图的放射性思考方法，除了加速资料的累积量外，更多的是将数据依据彼此间的关联性分层分类管理，使资料的储存、管理及应用更加系统化或者更有条理性，从而极大地提高了大脑运作的效率。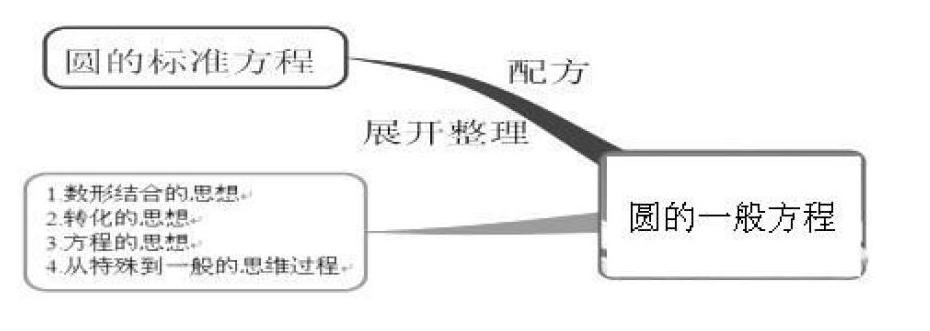

思维导图有四个基本的特征：（1）注意的焦点清晰地集中在中央图形上；（2）主题的主干作为分支从中央向四周放射；（3）分支由一个关键的图形或者写在产生联想的线条上面的关键词构成；（4）各分支形成一个连接的节点结构。因此思维导图在表现形式上是树状结构的。

2 思维导图在数学教学中的应用

新课标下的数学教学有别于传统的数学教学，需以学生为中心建立自主、合作、探究的学习模式。学习的效能取决于两个关键词，一个是“透彻”，另一个则是“系统”。然而，没有“深度思考”就不可能做到“透彻”，缺乏“系统思考”就不可能做到“系统”，也就是说关键是要解决“有效探究”的问题。思维可视化教学的出现很好的解决了这一困扰问题，它的“思考方法”主要包括提炼、区分、判断、推理、分析、综合等逻辑方法，还包括了分类讨论、数形结合、类比、概括与归纳、推论与演绎等数学思想方法，是自主、合作、探究学习模式整体“落地”的有力新支点。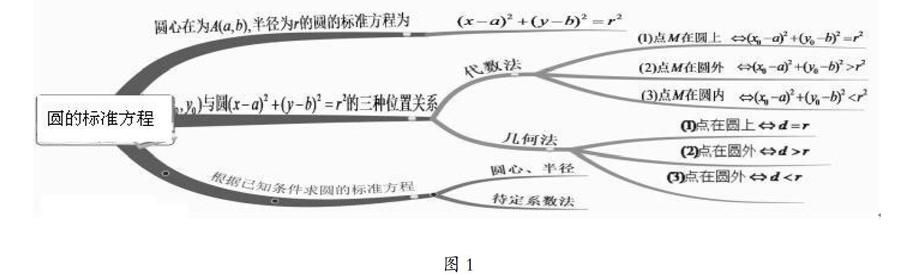

思维导图，能够清晰的的展示教师的思维过程，实现思维可视化，让学生明白知识与知识之间、知识与数学思想方法之间的联系，明白教师教学的整体思路，从而达到事半功倍的效果。下面我以高中数学人教A版必修2第四章第2小节的内容《圆的一般方程》为例，具体说明思维导图在数学教学中的应用。

在本堂课的教学中，贯彻以课前练习，巩固旧知→提出问题，创设情景→深入探究，获得新知→应用举例，巩固提高 →课堂练习，形成方法。小结反思，拓展引申的一条主线展开教学。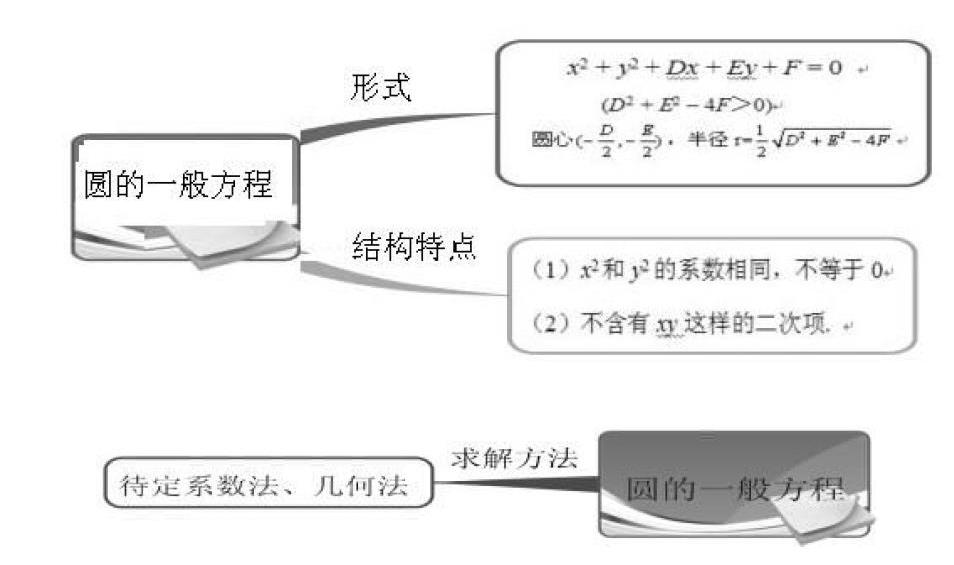

首先是对上一节课所学的《圆的标准方程》进行知识回顾，表现形式是让学生完成学案上的练习题并回顾上节课所画的思维导图（见图1）。

无序、重复、杂乱，这是当前习题教学存在的主要问题之一，忽视了习题教学目的的全面性和层次性。利用思维导图进行习题课，通过习题训练帮助学生完善知识建构的工作，以题型为主线，在学生复习过程中，运用思维导图，从基础知识入手理清思路，明确知识要点，对课程内容进行分类总结和复习。

接着又提出问题，我们知道直线的方程一定是一个二元一次方程，反之，二元一次方程也一定能表示直线.那么，圆的标准方程又是几元几次方程呢？反之是否成立？学生通过类比的思想，再结合实例，从特殊到一般尝试解决所提出的问题，初步可以探究出圆还有另外一种表现方式即圆的一般方程，也可以了解到圆的两种形式的方程之间还可以进行相互的转化。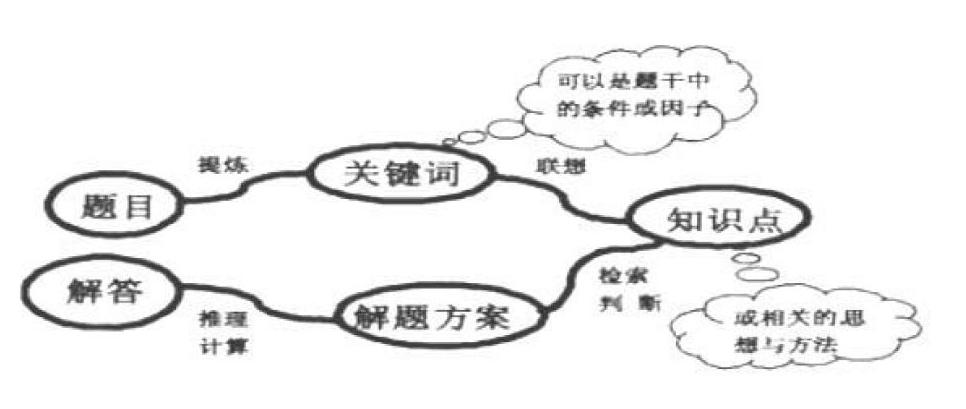

学生通过实例得出形如x2+y2+Dx+Ey+F=0的二元二次方程并不一定能表示圆，从而进入第三部分深入探究，获得新知，学生通过自主、合作、探究得出形如x2+y2+Dx+Ey+F=0的二元二次方程在满足什么条件下才能表示圆，其它条件下又表示怎样的几何图形；以及思考圆的一般方程与一般的二元二次方程Ax2+By2+Cxy+Dx+Ey+F=0 相比，有何特点，并解决圆的标准方程与一般方程之间的互化问题，解决学生在上一部分可能会提出的问题。

在实际的新课教学中，学生可以利用思维导图进行预习，以小组合作的形式，画出充满个性的思维导图，对教材内容进行整体感知。整个预习过程中学生的意见经过互相碰撞，新的观点不断产生，从而加深对新课的认识和理解。情况往往是学生当堂就可以向大家展示本组的学习成果。然后在预习的基础上，教师可以指导学生从不同的角度、不同的问题设问，运用思维导图总结教材内容，更深地理解教材深层结构，如：结构式、主题式、解题式、线索式、关键词式等等。最后学生通过小结，对本堂课进行全面的梳理，并画出思维导图（见图2）。由于人对图形形状及颜色的记忆比对文字的记忆更加深刻，因此，在用思维导图完成对本节课的小结后，学生更容易记住本节课的知识点以及思想方法。

3 思维导图在例题讲解中的应用

对题目思考的一般形式：

思维导图在例题讲解中的另一大重要作用是一题多解以及例题变式，这样的处理方式会使学生学会如何去联系相关知识点，从而实现的知识的拓展和思维的迁移。以本节课的例题为例：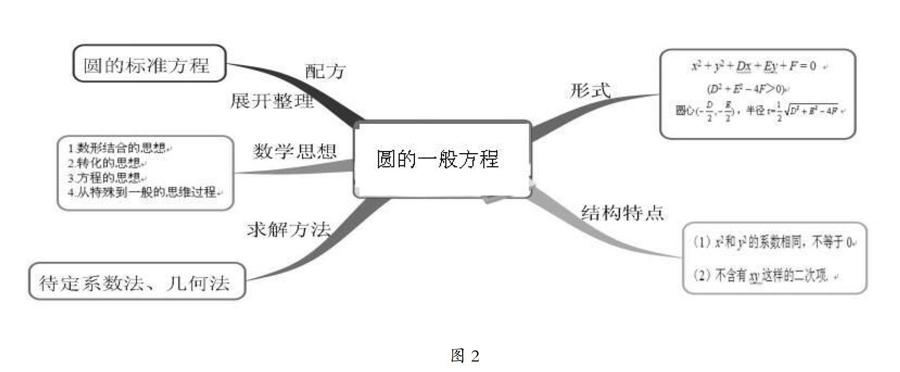

例题：求过三点A（1，3），B（4，2），C（1，-7）的圆的方程，并求这个圆的半径长和圆心坐标。

变式：（2015新课标2卷）过三点A（1，3），B（4，2），C（1，-7）的圆交y轴于M，N两点，则MN=（ ）

参考文献：

[1] 计雪娟，苗凤华.浅析思维导图在高中数学教学中的应用策略[J].数学学习与研究，2015，（1）.

[2] 黄坪，尹德好.高中数学题根[M].华东师范大学出版社.