小学数学教学中数形结合思想的渗透

林庆寿

摘 要： 数形结合思想是数学教学中重要的思想，它通过数与形的相互转化，将抽象的数学语言与直观的图形结合起来，以形助数，以数辅形，化繁为简，化抽象为具体，开拓学生的解题思路，使逻辑思维与形象思维完美地统一起来，促进学生有效地解决数学问题。

关键词： 小学数学教学 数形结合 渗透

数形结合思想就是通过数和形之间的对应关系和相互转化来解决问题的思想方法。“数”与“形”是数学研究的两个基本对象，利用“数形结合”方法能使“数”和“形”统一起来，借助于“形”的直观理解抽象的“数”、运用“数”细致入微地刻画“形”的特征，达到直观与抽象相互配合、取长补短，从而顺利、高效地解决数学问题。下面结合我的实际教学谈谈如何在小学数学教学中渗透数形结合思想。

一、备课时，挖掘数形结合思想适时渗透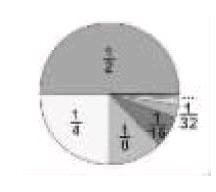

赞可夫说：“教会学生思考，这对学生来说，是一生中最有价值的本钱。”教会学生思考就是要教会学生掌握数学思想方法。小学常用的数学思想方法很多，而数形结合思想具有数学学科的鲜明特点，是解决许多数学问题的有效思想。因此，备课中，我们要深入挖掘教材中蕴含的数形结合思想，设计能有效引导学生经历知识形成过程的教学方法，让学生在观察、对比、分析、抽象、概括的过程中领悟数学知识蕴涵的思想。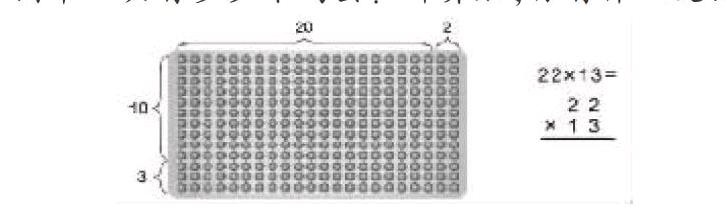

如教学六年级上册第八单元“数与形”这道题有无数个数相加，用学生现有的知识根本无法直接计算。备课中，教师应考虑到教学时要先引导学生观察加数的特点：每一项的分子都是1，每一项的分母都是它前一项分母的2倍；也可以说第几项的分母就是2的几次方，第n项就是2的n次方。接着引导学生联想到分数的计算可以用直观图表示，然后教师可以构造一个长度或者面积是1的图形（如圆形或正方形），如下图所示。先取它的一半作为二分之一，再取余下一半的一半作为四分之一，如此取下去……当取的次数很大很大时，余下的面积就非常小了，引导学生观察图形，想象当取的次数趋向于无穷大时，余下的部分就趋向于0，因而最后取的线段长（面积）是1。所以这题的得数是1。本题结合数轴和图形建立了一一对应关系，真正做到以形助数，帮助学生理解算理，在理解算理的基础上掌握计算方法，正所谓“知其然，知其所以然”。数与形的结合让学生进一步感受到“化数为形”的直观、形象、简洁的特点，在这一过程中，学生也体会到推理和极限的思想。

我们应该充分根据孩子们的认知规律，在教学过程中适时渗透数形结合思想，培养他们的数学思维能力。备课时，教师就要深入研究教材，吃透教材编排的意图，有效渗透数形结合思想，彰显数学学习的价值。

二、课堂上，巧用数形结合建构模型

“数无形时少直观，形少数时难入微”，利用数形结合，可以使某些抽象的数学问题直观化、生动化，使问题化难为易、化繁为简，激发学生学习兴趣。在教学中那些学生觉得难以理解的易出现错误或混淆的内容，教师可充分利用“形”，把抽象的问题变得直观、形象，丰富学生的表象，引发联想，引导学生探索规律，建构解题模型。

如我在教学五年级上册“植树问题”时，先以人人都有的手为素材，让学生伸出手观察，从而认识“棵树”与间隔数，渗透一一对应思想，为新课学习做好铺垫。接着出示例题：同学们在全长20m的小路一边植树，每隔5米栽一棵（两端要栽），一共要栽多少棵树？我先放手让学生自主探究，学生有的通过实践操作把牙签插在长条形橡皮泥上模拟种树，有的画线段图分析。接着我让学生在线段图中结合数字分析：20里面有4个5，每增加5米种1棵，加上开头的1棵，一共是5棵。这样加强了数与形之间的联系，化解了难点，从而得出解题模型，两端都种：棵数=间隔数+1。学生用前面探究的经验和方法继续自主探究，很快得出植树问题的另外两种解题策略，只种一端：棵数=间隔数，两端都不种：棵数=间隔数-1。

通过这样的“数形结合”，学生以后解题时看到算式眼前就会出现图形，见到图形就能联想到算式，对后面的练习就迎刃而解了。本课借助实际操作和画线段图的方法，正确理解植树棵数与间隔数之间的关系，化抽象为具体，使学生深刻理解题意，自主探究出解题模型，学生的思维发展有了凭借，数学思想方法真正得以渗透。

三、练习中，渗透数形结合提高能力

课堂练习是小学数学教学的重要组成部分，是学生数学学习必不可少的重要环节，是学生掌握知识，形成技能，发展智力的重要手段。因此，教师引导学生掌握理解课堂练习题是十分重要的。有些题目利用数形结合的方法，能让学生表象清晰，记忆深刻，对算理理解透彻，有利于提高学生的解题能力和思维能力。

例如教学三年级下册47页第1题时，我先引导学生观察点子方阵图，每行有22个鸡蛋，求13行有几个鸡蛋。把22分成20和2，13分成10和3，先算2×3=6，20×3=60，2×10=20，20×10=200（结合每步的算式在图中圈出对应的部分）。也就是说点子图由4部分组成，200+60+20+6=286。由此引导学生结合点子图完成右边算式的笔算。这样借助直观的图形学生理解了两位数乘两位数的算理，掌握了算法。计算完成后，还可以让学生看着算式解释图形，两者结合，真正做到“以形助数，以数解形”。

下图中一共有多少个鸡蛋？计算后，你有什么发现？

数与形是紧密联系、相辅相成的。在数学教学中渗透数形结合思想，不仅能提高学生分析能力、思维能力及解决数学问题的能力，还深深地影响着学生今后的数学学习和知识的应用。数形结合思想不可能一朝一夕形成，它需要长期渗透才能逐步让学生掌握。因此，教师要做教学的有心人，在具体的教学中有目的、有计划、有系统，适时适度地渗透，让数形结合思想始终贯穿在学生的数学学习过程中，成为一种有意识的教学活动。只有这样，数形结合思想方法的教学才能落到实处，数形结合思想才能作为学生学习数、运用数学和创造数学的有力工具。

参考文献：

[1]刘加霞，主编.小学数学课堂的有效教学.北京师范大学出版社，2008.6.

[2]教育部.义务教育数学课程标准.北京师范大学出版社，2011.

[3]王永春.小学数学与数学思想方法.华东师范大学出版社，2014.