二项分类logistic回归的基本原理和关键问题

刘彬彬 王琦琦 于石成 胡跃华 么鸿雁 孙谨芳 谭云洪



·流行病学与统计学方法·

二项分类logistic回归的基本原理和关键问题

刘彬彬 王琦琦 于石成 胡跃华 么鸿雁 孙谨芳 谭云洪

二项分类logistic回归是医学研究中常用的方法，优势比及其95%可信区间是logistic回归分析最重要的参数值，直接反映了自变量作用的大小和方向。而样本含量、自变量筛选、变量赋值和结果解释则是进行logistic 回归分析的关键问题，决定了回归分析是否能得到相对最佳的回归模型而准确反映自变量的影响作用，作者将就上述问题进行阐述。

回归分析； Logistic模型； 比值比

logistic回归是医学研究中常见的统计分析方法，可用于疾病危险因素分析、药物剂量反应研究、临床试验评价、疾病预后因素分析等诸多领域。当研究二分类观察结果与一组影响因素之间的关系时，如观察结果为是否患病、是否感染、是否死亡、是否复发等，最常用的多元统计学分析方法即为二项分类logistic回归分析。

logistic回归属于概率型非线性回归[1]，其最常用的模型参数是利用回归系数计算的优势比(odds ratio，OR)，该值反映了在剔除其他自变量的影响作用之后，自变量Xi对阳性结果发生的影响作用。ORi=1表示Xi对阳性结果的发生无作用，ORi>1表示Xi的暴露会导致阳性结果的发生率增加，ORi<1表示Xi的暴露会导致阳性结果的发生率降低。

在二项分类logistic回归的分析过程中，需要注意以下几个关键问题，以保证获得基于已有数据资源的最佳回归模型：

1. 样本含量的判断：logistic回归的所有统计推断要求保证足够的样本量[2]。随着模型中自变量个数的增加，自变量各水平的交叉组合数呈几何级数增加，样本量不足会影响模型的稳定性，出现异常的参数估计值[3]。1998年，Hsieh等[4]提出了logistic回归的样本含量计算公式。但logistic回归分析是在结果分析时应用的数据分析方法，医学研究中还是应综合考虑研究类型(包括横断面研究、病例-对照研究、队列研究等)和设计方法(包括抽样、分层、配对等)等因素来计算样本含量。在进行logistic回归分析时，可根据以下条件评估样本含量对模型适用性和稳定性的影响：(1)病例组和对照组应至少各有30～50例，模型中自变量的个数越多，需要的样本例数也相应越多[2]；(2)各个自变量亚组的样本含量应大于自变量总数的20倍[3]；(3)阳性结局(结果变量为二分类)发生率小于50%时，每一个自变量至少需要10例具有阳性结局的样本[3]。

如表1所示，利用logistic回归分析肺结核患者耐药情况的影响因素。纳入肺结核患者200例，其中64例耐药(病例组)，136例敏感(对照组)，满足上述条件1；考虑纳入性别和学历2个自变量进入分析，各个亚组的样本量均大于40，满足上述条件2；阳性结局(耐药)发生率为32%(64/200×100%)，各个亚组耐药者例数均大于20(性别和学历2个自变量)，满足上述条件3。综上，可认为利用该数据满足logistic回归的样本量要求，可建立较稳定的模型。

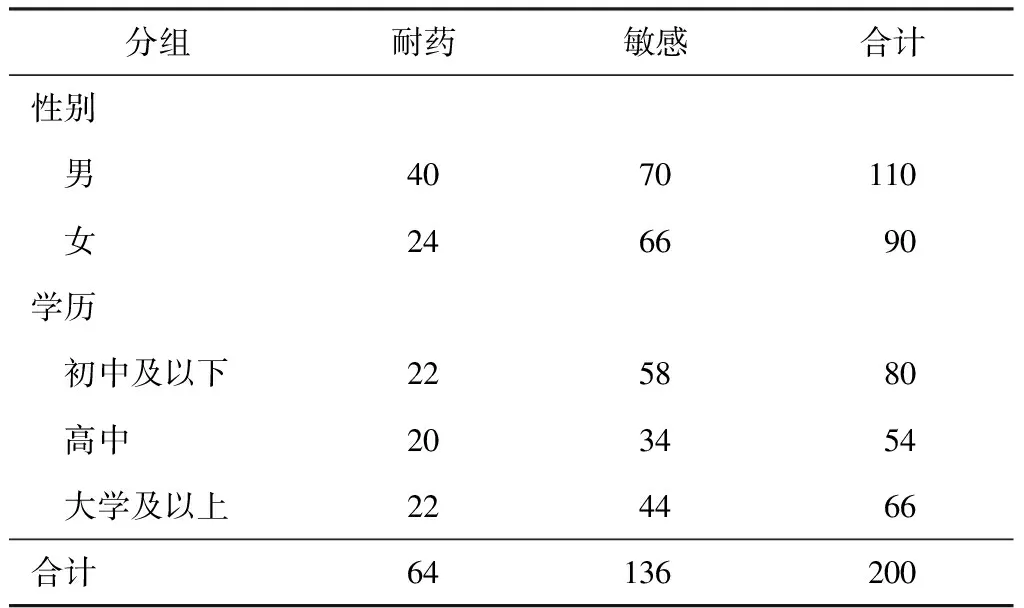
表1 肺结核患者耐药情况分析的分组信息(例)

2. 自变量的选择：为了使所建立的logistic回归模型比较稳定和便于解释，自变量的选择非常重要，应尽可能将对结局变量影响大的自变量选入模型中，将作用不显著的自变量排除在外[2]。

首先，应结合专业知识和研究目的评估自变量的重要性，选择可能会影响结果的因素作为分析变量。其次，根据卡方检验进行单因素分析，选择有统计学意义的变量纳入回归模型(也可使用“单因素logistic回归分析”，其作用等价于卡方检验[5])。

单因素分析结果具有统计学意义的k个自变量中最终纳入哪些变量进入回归模型，是logistic回归分析最关键的步骤。全局择优法是对自变量各种不同组合所建立的回归方程进行比较，从中挑出一个“最优”的回归方程[2]。在实际应用中最常使用的是逐步选择法，在统计分析软件中的应用也最方便，包括前进法、后退法和逐步回归法3种[2]。

此外，还可根据变量的专业意义和研究目的构建模型，按照研究关注的主要影响因素、常见的混杂因素(如性别、年龄)、对观察结果作用明确的影响因素(如吸烟对肺癌的作用)、证据力度较弱的影响因素和可能但尚无证据支持的影响因素的顺利依次加入，并利用回归模型的评价指标[3][包括皮尔逊χ2、偏差(deviance)、Homser-Lemeshow 统计量(H-L统计量,即拟合优度指标)、赤池信息准则(Akaike information criterion，AIC)和施瓦茨准则(Schwarz criterion，SC)、广义确定系数R2]判断当前模型是否已满足研究要求。

3.自变量的赋值：在进行logistic回归分析时，自变量的赋值是一个关键的环节。不同的变量赋值形式，可能导致回归模型参数的符号、大小和含义发生变化[2]。自变量包括分类变量、等级变量和连续变量，变量赋值形式各有不同。

分类变量，例如职业、学历、血型等，在数据整理时通常整理为数值型变量，即用1，2，3，…k，k表示k个不同的种类。这里的数值实际上只是分类的一个代码，无大小关系，所以需要将取值范围为k的分类变量，转化成k-1个哑变量纳入回归模型[3]。

等级变量，如人体血清反应强度分-、±、+、++、+++、++++六级，药物治疗的效果包括治愈、显效、好转、无效四级，可以以连续变量的形式进入logistic回归模型，得到自变量每改变1个等级时的OR值。但这样处理的前提条件是自变量的等级分组与应变量的改变情况呈线性关系，其效应呈等比例改变[3]。如果该前提不满足，则只能将等级变量作为分类变量，通过设置哑变量进行分析。

连续变量，如年龄、血压、白细胞计数等，在数据整理时一般以原始观察值记录，如将连续变量直接带入logistic回归，则OR值表示自变量每改变1个单位，阳性结果的发生情况较之前水平的改变倍数。但这种情况有时在专业上比较难理解，比如年龄，OR值表示每增加1岁时的改变情况，不一定具有临床意义[3]。此时应将变量按值大小分成几组，按等级变量的处理办法，直接纳入或化作k-1个哑变量纳入模型。

4. 哑变量的应用：设置哑变量必须先选取一个参照水平，表2是以“水平1”为参照，得到表示其他2个水平的哑变量D1和D2。其中D1=1表示学历分组为高中，D1=0表示学历分组为非高中，D2含义类似(大学及以上)。当D1和D2均等于0时，表示学历分组为初中及以下(参照水平)。

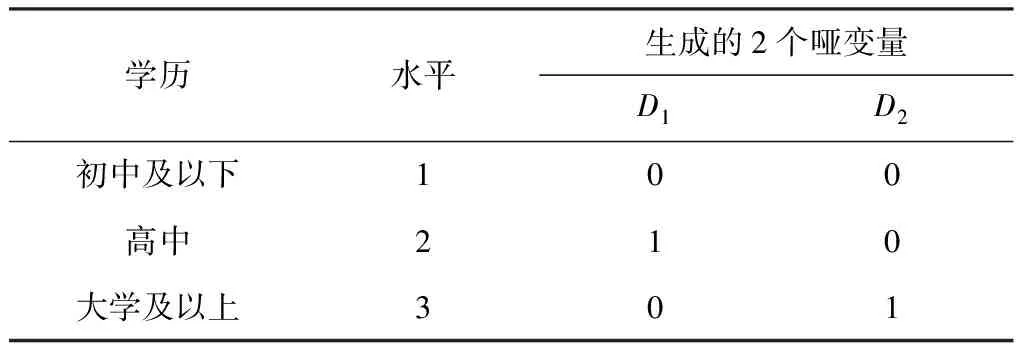
表2 哑变量的设置方法

哑变量反映了同一个多分类变量不同水平的影响作用，是一个整体变量。因此，logistic回归模型对哑变量应该遵循同进同出的原则[3]。即当同一个多分类变量生成的一组哑变量中，如果其中有至少1个哑变量进入了回归模型，此时就不能按照逐步选择法将该组中其他无统计学意义的哑变量剔除，而应该采用强制进入的处理方式，将该组哑变量全部纳入模型。以表3为例，由学历生成的2个哑变量，按照0.05的检验水准，高中(D1)有统计学意义，大学及以上(D2)尚未观察到有统计学意义，但这2个哑变量都应该纳入回归模型。

表3 logistic回归分析的结果

Variables in the Equation

图1 SPSS软件进行logistic回归分析的主要结果项目

哑变量的参数表示的是一个多分类变量的各个水平与参照水平相比，对观察结果的影响作用。此作用的大小和方向会因为选择的参照不同而改变，因此需要根据研究目的和专业背景选择合适的参照组。表2是以最低学历为参照水平，分析其他2个学历相比于最低学历各自的影响作用。假设在进行某种特殊疾病的发病风险分析时，基于专业知识可以初步认为该疾病在低学历和高学历时都可能高发，同时研究也希望对两个学历水平的影响作用大小进行评估，此时就可考虑选择高中组为参照水平，计算低学历(初中及以下)和高学历(大学及以上)相对于参照水平的OR值。

5. 应变量的赋值：应变量的赋值也是影响研究结果的关键问题之一。当观察结果为二分类变量时，一般阳性结果赋值为1，阴性结果赋值为0，所得OR值大于1为危险因素，小于1为保护因素。但实际上这其中包含了阳性结果是不利结局的假设，如患病、死亡、复发。当阳性结果是有利结局时，如治愈、主动求医，自变量的性质则会得到恰恰相反的结论。需要注意的是，在利用SAS软件进行logistic回归分析时，系统默认计算的是较小值与较大值比较的风险，与上述分析习惯刚好相反，在赋值时应做相应改变[3]。

在结果报告时，不鼓励直接将图1的软件分析结果直接复制纳入，需要将表头转换成标准的参数名称或符号，并标明变量的亚组信息(表3)。如前所述，OR值及其95%可信区间是logistic回归分析中最常用的参数，当篇幅有限时可以其为主要内容进行报告。

表3展示了以下结果：性别和学历对结核病患者耐药情况有影响。相对于女性，男性是耐药的危险因素，OR值为7.732(95%CI：1.589～37.615)。相对于初中及以下组，高中学历是耐药的危险因素，OR值为5.139(95%CI：1.215～21.737)；相对于初中及以下组，尚不能认为大学及以上学历对结核病患者耐药有影响。

综上，医学研究常用logistic回归分析观察结果与影响因素间的关系，变量赋值、自变量选择和结果解释都是logistic回归分析成功与否的重要影响因素。需要强调的是，不能盲目开展logistic回归分析，需要结合专业知识，在明确研究目的的基础上，依据科学的数学原理对数据进行分析，实事求是地解释，才能得到相对最佳的回归模型，获得准确而又有实际意义的结果。

[1] 方积乾.卫生统计学. 7版.北京: 人民卫生出版社, 2012.

[2] 孙振球, 徐勇勇. 医学统计学. 4版.北京: 人民卫生出版社, 2014.

[3] 冯国双, 刘德平. 医学研究中的logistic回归分析及SAS实现. 2版.北京: 北京大学医学出版社, 2015.

[4] Hsieh FY, Bloch DA, Larsen MD. A simple method of sample size calculation for linear and logistic regression. Stat Med, 1998, 17(14):1623-1634.

[5] 李锡太, 叶临湘, 施侣元, 等. 肺结核复发危险因素logistic回归分析. 中华流行病学杂志, 2004, 25(8): 658-660.

[6] 宇传华. SPSS与统计分析. 2版.北京: 电子工业出版社, 2012.

(本文编辑：李敬文)

Principle and key steps of binary logistic regression

LIUBin-bin*,WANGQi-qi,YUShi-cheng,HUYue-hua,YAOHong-yan,SUNJin-fang,TANYun-hong.

*DepartmentofLaboratory,Hu’nanInstituteforTuberculosisControl,Hu’nanChestHospital,Changsha410013,China

s:SUNJin-fang,Email:sunjf@chinacdc.cn;TANYun-hong,Email:tanyunhong@163.com

Binary logistic regression analysis is frequently used in medical researches, odds ratio (OR) and 95% confidence index, which can directly measure the effect of independent variable on the responsing variables, which are the most important indicators of logistic regression analysis. Sample size, variable selection, variable assignment and result interpretation are the key steps to construct an optimal model, which can reflect the influence of explanatory variables correctly, and they will be discussed especially in this thesis.

Regression analysis; Logistic models; Odds ratio

10.3969/j.issn.1000-6621.2016.08.002

中国疾病预防控制中心青年科研基金课题(2015A204、2016A201)

410013 长沙，湖南省结核病防治所 湖南省胸科医院检验科(刘彬彬、谭云洪)；中国疾病预防控制中心流行病学办公室(王琦琦、于石成、胡跃华、么鸿雁、孙谨芳)

孙谨芳，Email: sunjf@chinacdc.cn；谭云洪，Email:tanyunhong@163.com

2016-07-05)