基于聚类选择k近邻的LLE算法及故障检测

薄翠梅，韩晓春，易辉，李俊（南京工业大学电气工程与控制科学学院，江苏 南京 211816）



基于聚类选择k近邻的LLE算法及故障检测

薄翠梅，韩晓春，易辉，李俊
（南京工业大学电气工程与控制科学学院，江苏 南京 211816）

摘要：针对化工过程在多种运行模式下多种流形结构具有不同最优近邻数问题，提出了基于聚类选择k近邻的局部线性嵌入（LLE）过程监控方法。使用LLE算法提取高维数据的低维子流形，通过局部线性回归得到高维数据空间到特征空间的映射矩阵；选择Silhouette指标作为聚类有效性指标评估嵌入空间样本信息的相似性，进而确定最优近邻数，根据映射矩阵构建故障监控统计量及其控制限,进行故障检测。最后将所提算法与其他经典算法应用于TE化工过程对比分析，验证了算法的有效性。

关键词：局部线性嵌入；最近邻数；子流形；故障检测；聚类指标

2015-12-24收到初稿，2016-01-06收到修改稿。

联系人及第一作者：薄翠梅（1973—），女，教授。

引 言

现代化工过程中存在强非线性、强耦合性和多模态等特性，使得过程数据不能直接反映其运行状态，需要提取有效数据进行分析[1]。传统的线性降维算法，如PCA[2]，保持了数据集的全局距离结构不变，不能保持非线性数据结构的内在流形。基于核函数的非线性降维算法，如KPCA[3]，采用核函数将数据映射到非线性空间，增加了计算复杂度。基于流形的非线性降维算法，如等距映射（ISOMAP）[4]、局部线性嵌入（LLE）[5]、邻域保持嵌入（NPE）[6]等，通过保持数据的几何结构，发现嵌入在高维数据中的低维特征，引起了广泛的关注。

在LLE算法[7]中，需要人为设定两个自由参数，即嵌入空间的维数d和最近邻个数k，其中后者的选择对嵌入结果和映射质量有很大影响[8]。在故障诊断过程中，由于故障类别的多样性，原始数据集在空间中呈间断性分布[9]，在用k近邻构建邻域图时，如果数据集的近邻数选取不当，将导致投影到低维空间的故障信息不能保持原始数据的几何结构的完整性[10]。当k较小时，数据将会被分割成多个较小的邻域而无法反映数据连续的局部几何特征，k较大时，会将不相关的数据点划分到一个邻域内[11]。

本文针对非线性化工过程中数据类型的多样性，提出了基于聚类算法选择最近邻数k的LLE算法，并将其应用到故障检测中。

1 基于聚类选择k近邻的局部线性嵌入算法

局部线性嵌入算法是流形学习算法中非线性降维算法，其基本思想是采用局部线性化方法，构建局部线性超平面，将高维数据空间映射到低维空间中，保持局部流形结构不变，通过相互重叠的局部邻域信息来表达整体集合性质[12]。

不同类别模式的数据位于不同的流形结构上，当选择相同的近邻数时，其降维的效果不同[13]。本文对Swiss Roll、Sphere、Twin Peaks数据集及当k取不同值时进行LLE降维后的投影流形进行仿真研究，如图1所示。图1(a)为Swiss Roll数据集及当k= 6，16，20时，通过LLE降维后的投影流形，图1(b)为Sphere数据集及当k = 2，6，16时的投影流形，图1(c)为Twin Peaks数据集及当k = 6，16，20时的投影流形。从图中可以看出，当k分别为16、6、20时，Swiss Roll、Sphere、Twin Peaks的降维效果最好。

1.1 局部线性嵌入算法

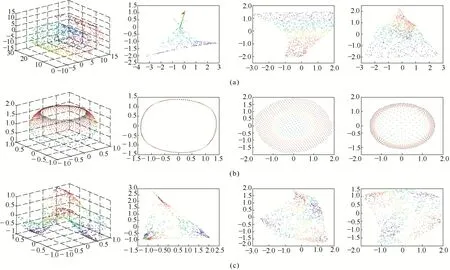
图1 人工数据集及其LLE降维Fig.1 Artificial datasets and projection performed LLE algorithm

（1）构造邻域连接图：对于每个样本点，采用欧式距离确定它k个近邻。

（2）重构权值矩阵W：在每个样本点及它的邻域点之间重构权向量，使误差函数ε(Wi)达到最小。

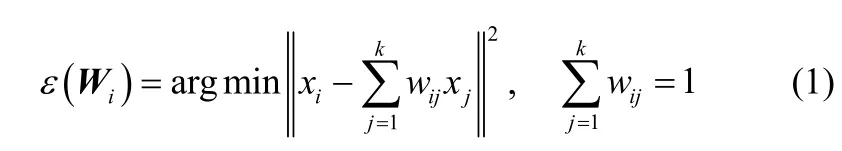
如果xj不属于xi的近邻，则。

（3）计算嵌入矩阵：通过权值矩阵W使损失函数ε(Y)最小化计算嵌入矩阵Y。损失函数及其约束条件为

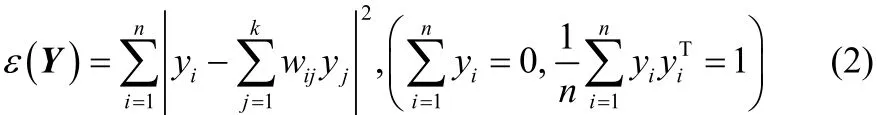
1.2 LLE投影

局部线性嵌入算法不能直接将高维数据空间投影到低维空间中，新的样本数据要通过映射矩阵投影到低维空间中。映射矩阵可以通过求解线性平方回归问题得到[15]

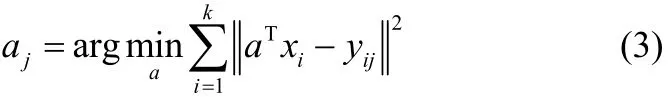
其中1≤ j≤ d，yi是低维空间的嵌入坐标，yij是yi的第j个变量。

新的样本数据xnew可以通过ynew= Axnew计算新的嵌入坐标ynew。

1.3 基于聚类算法选择k近邻

针对不同数据结构最优近邻数不同的问题，将选择k近邻数看作选取最优聚类数[16]。根据系统模型的聚类有效性指标确定最优聚类结果所对应的聚类数目，即最佳聚类数kopt[17]。Silhouette指标反映了聚类结构的类内紧密性和类间分离性。

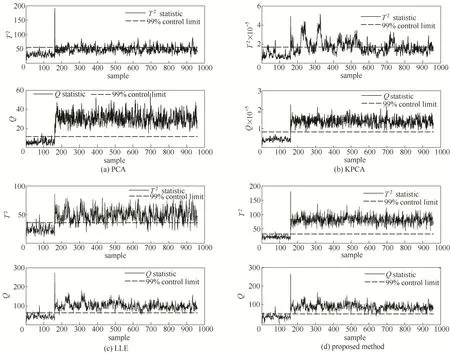
图2 故障4的监控结果Fig.2 Monitoring results of fault 4

Silhouette指标Sil可以表示如下

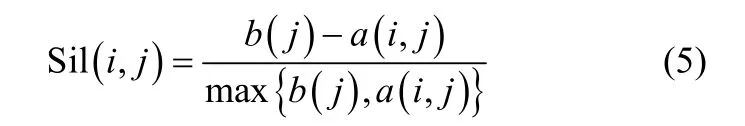
所有样本的平均Silhouette指标值越大表示聚类质量越好，其最大值对应的类数为最佳聚类数，即kopt可以通过式（6）确定

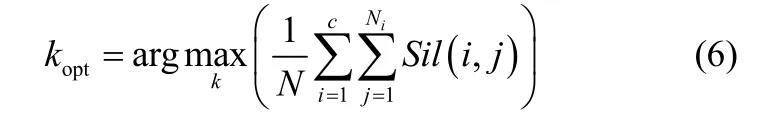
式中，N为所有样本的个数，Ni是类别i中训练样本的个数，。

2 过程监控

2.1 构造故障监控统计量

将LLE算法应用到故障监控中，分别对低维数据空间的特征空间和残差空间构造T2和Q统计量[18]，T2和Q统计量的定义公式为

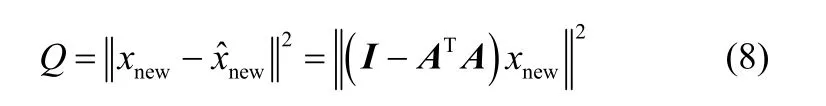
式中，ynew为观测数据xnew在LLE空间的投影，可以通过ynew= Axnew计算得到；S是正常状态下嵌入矩阵Y的协方差矩阵，即T/(N 1)=− S Y Y。T2和Q统计量的控制限为

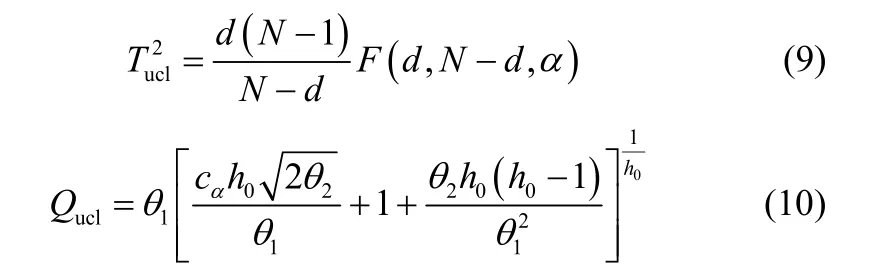
式中，F( d , N− d , α )为自由度为d和N− d置信水平为α的F分布。λ为协方差矩阵S的特征值，cα是正态分布在检验水平为α下的临界值。当或者Q＞ Qucl时，检测故障发生。

2.2 故障检测步骤

图3 故障5的监控结果Fig.3 Monitoring results of fault 5

利用监控统计量对故障数据集的特征空间和残差空间进行在线监控。

2.2.1 离线建模

（1）选择最优聚类数k的搜索范围[kmin, kmax]，其中kmin= 2，kmax= int(N )，确定固有维数d，并设Sil= 0。

（2）对数据样本X进行标准化处理，根据LLE算法计算嵌入矩阵Y和投影矩阵A。

（3）对故障观测数据集X'进行标准化处理，根据Y'= AX'计算其嵌入坐标Y'。

（4）根据式（5）计算Y'所有样本Silhouette指标Sil。

2.2.2 在线检测

（1）确定kopt，根据正常数据的均值和方差对Xnew进行标准化处理。

（2）采用LLE算法进行特征提取及投影。

（3）计算T2和Q统计量，判断是否超过其相应的控制限。

3 TE过程仿真研究

Tennessee-Eastman（TE）[19]过程是一个实际工艺流程的标准测试过程，运行代码和故障数据来源于http://depts.washington.edu/control/LARRY/TE/down load.html#Topics。本文选取40个测量变量和12个操作变量用于过程监控，将所提算法与PCA、KPCA 和LLE算法相对比，采用方差贡献度确定主元个数，设定方差贡献率为0.85。在LLE模型中，设定近邻个数选为k = 33，低维特征空间的维数为d= 14，统计量置信度为0.99[20]。

图2和图3分别绘出了这4种方法对故障4、5的监控图。故障4和5分别为反应器和冷凝器冷却水入口温度阶跃扰动。从这3个故障监控图中可以看出所提算法的检测得到了非常明显的提升，特别是特征空间上的T2统计量与其他算法相对比具有较好的监控效果。

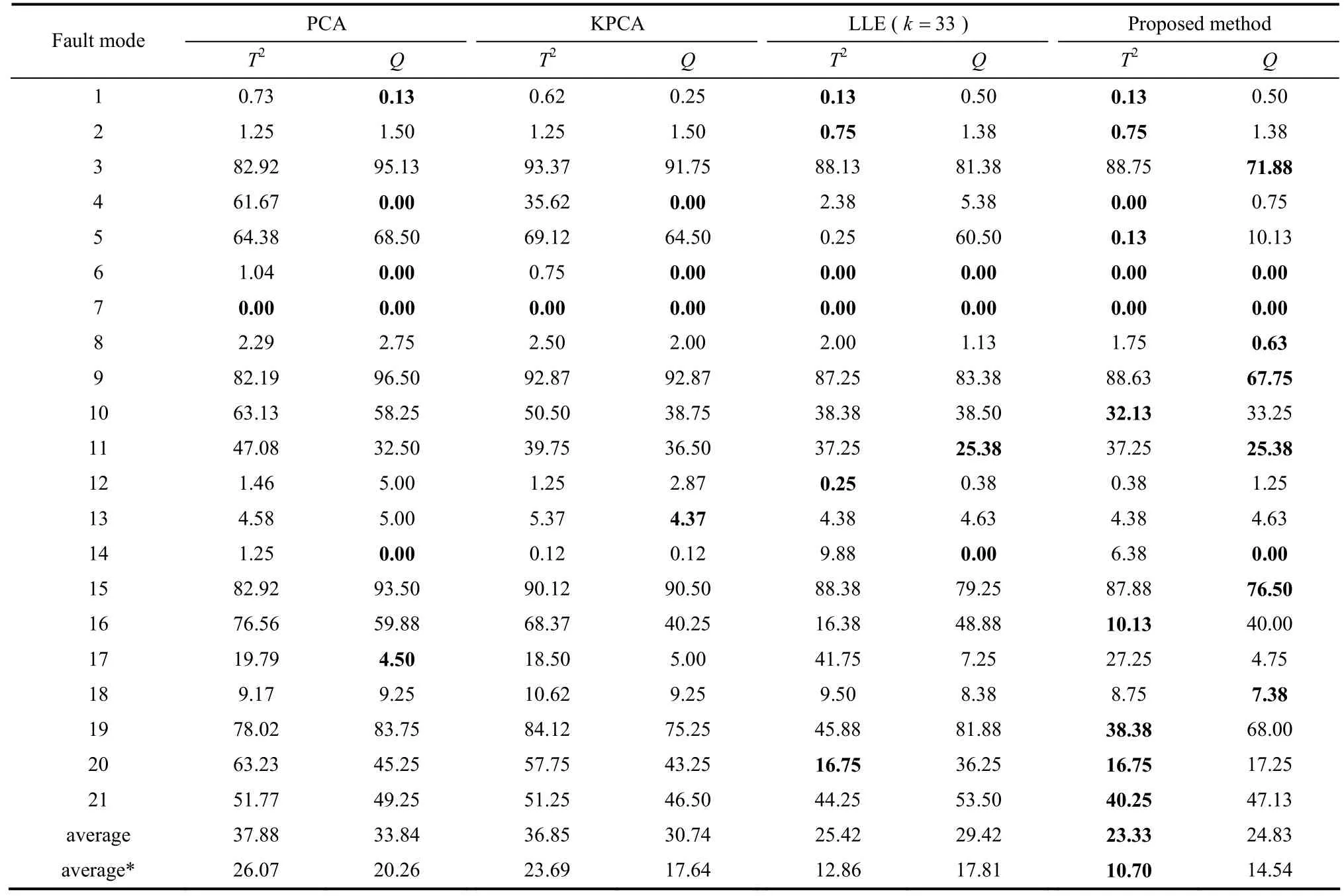
表1 TE过程故障数据集的误报率Table 1 False alarm rate of fault database in TE process

本文将这4种算法对TE过程的21种故障进行了测试，采用误报率作为故障检测效果的评价标准，计算了TE过程的21种故障的误报率，结果见表1。从表中可以看出，对于故障4、5、8、9、10、19、20、21，与其他3种算法相对比，本文所提算法具有更好的检测效果。针对每一个故障，误报率最低的值用粗体表示，所提算法的最优检测率最多，而且T2统计量的平均误报率（average）及排除故障3、9、15之后的平均误报率（average*）在这4种算法中最小，说明检测效果较好。

4 结 论

复杂化工过程具有多种的运行模式，不同流形的数据样本结构具有不同的最优近邻数，本文根据不同的数据类型，把选择k近邻数看作选取最优聚类数，根据聚类有效性指标计算合适的聚类数，通过映射矩阵降到低维空间，构建T2和Q统计量模型进行故障监控。在TE化工过程采用4种过程监控方法进行对比，结果表明所提算法比其他算法具有更好的故障检测性能。

References

[1] 王健, 冯健, 韩志艳. 基于流形学习的局部保持PCA算法在故障检测中的应用 [J]. 控制与决策, 2013, 28 (5): 683-687. DOI:10.13195/ j.cd.2013.05.46.wangj.025.

WANG J, FENG J, HAN Z Y. Locally preserving PCA method based on manifold learning and its application in fault detection [J]. Control and Decision, 2013, 28 (5): 683-687. DOI: 10.13195/j.cd.2013.05.46. wangj.025.

[2] 王晶, 刘莉, 曹柳林, 等. 基于核Fisher包络分析的间歇过程故障诊断 [J]. 化工学报, 2014, 65 (4): 1317-1326. DOI: 10.3969/j.issn.0438-1157.2014.04.023.

WANG J, LIU L, CAO L L, et al. Fault diagnosis based on kernel Fisher envelope surface for batch processes [J]. CIESC Journal, 2014, 65 (4): 1317-1326. DOI: 10.3969/j.issn.0438-1157.2014.04.023.

[3] JIANG Q C, YAN X F. Nonlinear plant-wide process monitoring using MI-spectral clustering and Bayesian inference- based multiblock KPCA [J]. Journal of Process Control, 2015, 32 (1): 38-50. DOI: 10.1016/j.jprocont.2015.04.014

[4] 张妮, 田学民, 蔡连芳. 基于RISOMAP的非线性过程故障检测方法 [J]. 化工学报, 2013, 64 (6): 2125-2130. DOI: 10.3969/j.issn.0438-1157.2013.06.031.

ZHANG N, TIAN X M, CAI L F. Non-linear process fault detection method based on RISOMAP [J]. CIESC Journal, 2013, 64 (6): 2125-2130. DOI: 10.3969/j.issn.0438-1157.2013.06.031.

[5] YANG X F, GOH A, QIU A Q. Locally linear diffeomorphic metric embedding (LLDME) for surface-based anatomical shape modeling [J]. Neuroimage, 2011, 56 (1): 149-161. 10.1016/j.neuroimage.2011.01.069.

[6] MIAO A M, GE Z Q, SONG Z H, et al. Nonlocal structure constrained neighborhood preserving embedding model and Its application for fault detection [J]. Chemometrics and Intelligent Laboratory Systems, 2015, 142: 184-196. DOI:10.1016/j.chemolab. 2015.01.010.

[7] JING C, YANG L. Locally linear embedding: a survey [J]. Artificial Intelligence Review, 2011, 36 (1): 29-48. DOI: 10.1007/s10462-010-9200-z.

[8] SHAN R F, CAI W S, SHAO X G. Variable selection based on locally linear embedding mapping for near-infrared spectral analysis [J]. Chemometrics and Intelligent Laboratory Systems, 2014, 131: 31-36. DOI:10.1016/j.chemolab.2013.12.002.

[9] SLUBAN B, LAVRAČ N. Relating ensemble diversity and performance: a study in class noise detection [J]. Neurocomputing, 2015, 160: 120-131. DOI: 10.1016/j.neucom.2014.10.086.

[10] XIE X X, HU J Z, XU F Y, et al. A fault diagnosis method using multi-manifold learning based on locally linear embedding [J]. Chinese Journal of Mechanical Engineering, 2013, 49 (11): 79-83. DOI: 10.3901/JME.2013.11.079.

[11] ANDRÉS Á-M, JULIANA V-A, GENARO D-S, et al. Global and local choice of the number of nearest neighbors in locally linear embedding [J]. Pattern Recognition Letters, 2011, 32 (16): 2171-2177. DOI: 10.1016/j.patrec.2011.05.011.

[12] WANG J. Real local-linearity preserving embedding [J]. Neurocomputing, 2014, 136 (20): 7-13. DOI: 10.1016/j.neucom.2014. 01.040.

[13] HETTIARACHCHI R, PETERS J F. Multi-manifold LLE learning in pattern recognition [J]. Pattern Recognition, 2015, 48 (9): 2947-2960. DOI: 10.1016/j.patcog.2015.04.003.

[14] 马玉鑫, 王梦灵, 侍洪波. 基于局部线性嵌入算法的化工过程故障检测 [J]. 化工学报, 2012, 63 (7): 2121-2127. DOI: 10.3969/j.issn. 0438-1157.2012.07.018.

MA Y X, WANG M L, SHI H B. Fault detection for chemical process based on locally linear embedding [J]. CIESC Journal, 2012, 63 (7): 2121-2127. DOI: 10.3969/j.issn.0438-1157. 2012.07.018.

[15] LI B W, ZHANG Y. Supervised locally linear embedding projection (SLLEP) for machinery fault diagnosis [J]. Mechanical Systems and Signal Processing, 2011, 25 (8): 3125-3134. DOI: 10.1016/j.ymssp. 2011.05.001.

[16] 周世兵, 徐振源, 唐旭清. 新的k均值算法最佳聚类数确定方法[J]. 计算机工程与应用, 2010, 46 (16): 27-31. DOI: 10.3778/j.issn.1002-8331.2010.16.008.

ZHOU S B, XU Z Y, TANG X Q. New method for determining optimal number of clusters in k-means clustering algorithm [J]. Computer Engineering and Applications, 2010, 46 (16): 27-31. DOI: 10.3778/j.issn.1002-8331.2010.16.008.

[17] ZHOU C Y, CHEN Y Q. Improving nearest neighbor classification with cam weighted distance [J]. Pattern Recognition, 2006, 39 (4): 635-645. DOI: 10.1016/j.patcog.2005.09.004.

[18] SAKTHIVEL N R, NAIR B B, ELANGOVAN M, et al. Full length article: comparison of dimensionality reduction techniques for the fault diagnosis of mono block centrifugal pump using vibration signals [J]. Engineering Science and Technology, 2014, 17 (1): 30-38. DOI: 10.1016/j.jestch.2014.02.005.

[19] CHEN H H, TIŇO P, YAO X. Cognitive fault diagnosis in Tennessee Eastman process using learning in the model space [J]. Computers and Chemical Engineering, 2014, 67: 33-42. DOI: 10.1016/j.compchemeng. 2014.03. 015.

[20] 宋冰, 马玉鑫, 方永锋, 等. 基于LSNPE 算法的化工过程故障检测 [J]. 化工学报, 2014, 65 (2): 620-627. DOI: 10.3969/j.issn.0438-1157.2014.02.036.

SONG B, MA Y X, FANG Y F, et al. Fault detection for chemical process based on LSNPE method [J]. CIESC Journal, 2014, 65 (2): 620-627. DOI: 10.3969/j.issn.0438-1157.2014.02.036.

研究论文

Received date: 2015-12-24.

Foundation item: supported by the National Natural Science Foundation of China (61203020, 61503181) and the Natural Science Foundation of Jiangsu Province (BK20141461, BK20140953).

Neighborhood selection of LLE based on cluster for fault detection

BO Cuimei, HAN Xiaochun, YI Hui, LI Jun
(College of Electrical Engineering and Control Sciences, Nanjing Tech University, Nanjing 211816, Jiangsu, China)

Abstract:In the process of chemical engineering, multiple manifold structures has different optimal number of nearest neighborhood under various operating modes. Locally linear embedding (LLE) algorithm based on clustering to select the nearest neighborhood is proposed for nonlinear monitoring. LLE algorithm was performed for dimensionality reduction and extract the available information in high-dimensional data. The mapping matrix from data space to feature space was obtained by local linear regression. The Silhouette index was selected as the clustering validity index to estimate the similarity between the embedded sample information, and further determine the optimal number of neighbors. Process monitoring statistics and its control limits were built based on the mapping matrix. Finally, the feasibility and efficiency of the proposed method were illustrated through the Tennessee Eastman process.

Key words:locally linear embedding; the number of nearest neighbor; sub-manifold; fault detection; clustering index

DOI：10.11949/j.issn.0438-1157.20151963

中图分类号：TP 277

文献标志码：A

文章编号：0438—1157（2016）03—0925—06

基金项目：国家自然科学基金项目（61203020，61503181）；江苏省自然科学基金项目（BK20141461，BK20140953）。

Corresponding author:Prof. BO Cuimei, lj_bcm@163.com