即时局部建模在填料塔液泛气速预测的应用

周丽春，靳鑫，刘毅，高增梁，金福江（华侨大学信息科学与工程学院，福建 厦门 360；浙江工业大学过程装备及其再制造教育部工程研究中心，浙江 杭州 3004）



即时局部建模在填料塔液泛气速预测的应用

周丽春1，靳鑫2，刘毅2，高增梁2，金福江1
（1华侨大学信息科学与工程学院，福建 厦门 361021；2浙江工业大学过程装备及其再制造教育部工程研究中心，浙江 杭州 310014）

摘要：填料塔在工业生产中应用广泛，准确预测填料塔的液泛气速具有重要的应用价值。实际的填料类型多种多样，获取的填料数据也存在差异，单一全局模型的预测效果受到一定的限制。首先给出了岭参数极限学习机模型及其节点增加的递推算法，以有效更新在线模型。结合即时学习方式，提出了局部递推岭参数极限学习机在线建模方法，用于填料塔液泛气速的预测。实验结果表明所提出方法能更充分挖掘数据间的相关信息，预测效果优于相应的全局模型。关键词：非线性系统；动态建模；神经网络；递推算法；极限学习机；系统工程

2015-12-24收到初稿，2015-12-30收到修改稿。

联系人：刘毅。第一作者：周丽春（1978—），女，讲师。

引 言

填料塔具有生产能力大、压力降小、操作弹性大等优点，在石油化工、精细化工、医药、环保等行业广泛应用。液泛的发生是现有工业填料塔分离操作存在的主要问题，降低了生产效率，严重时甚至会引起停车，影响整个生产系统的正常操作[1]。液泛是逆流填料塔中气液两相交互作用达到的一种特定的流体力学现象。当操作气速过大时，塔内的液体无法正常向下流，过多地积聚于填料间，并逐渐形成倒流，产生液泛。实际上，液泛是难以预测的，当液泛发生时，一般会出现压降急剧增加和效率急剧降低的现象。通常认为液泛气速是液泛发生时的气速，即填料塔的极限气速，是计算填料塔最大承载能力和塔径的必要参数[1-7]。因此，准确预测液泛气速和进行液泛监测具有重要的应用意义。

目前，实际生产中液泛气速的预测主要依靠传统的经验公式和压降通用关联图[3]。但是这些经验模型都需特定的填料常数，其通用性较差。另外，随着各种新型填料的出现，许多条件与经验公式并不相符，使模型的预测效果降低。考虑到传统液泛预测模型的准确程度和适用范围，大多数填料塔的设计和操作指标远低于最大有效能力，这难以满足目前激烈的市场竞争和需求。因此，有必要建立一种通用性好、准确度高的液泛预测模型。

随着过程数据能够及时获得，数据驱动的建模方法得到广泛研究和应用[8]，但用于液泛气速预测的却很少。Piche等[4]通过BP神经网络（backing propagation neural networks，BP-NN）来提高模型的通用性和预测的准确性，效果优于传统的经验公式。杨捷[7]通过径向基NN（radial basis function NN，RBF-NN）建立液泛气速预测模型，其预测性能优于BP-NN和传统的经验模型。极限学习机（extreme learning machine，ELM）是一种新型单隐层前馈神经网络（single-hidden-layer feedforward neural networks，SLFNs）。与传统神经网络不同的是，其隐层中的参数没有直接的关联，只要随机赋予输入权值和隐层节点的阈值，并且应用Moore-Penrose方法获得隐层输出矩阵的广义逆，通过一步计算即可确定网络的输出权值。ELM有较好的建模准确程度，同时可提高学习速度[9-17]。

然而，实际生产填料种类繁多，所收集的液泛数据较少，具有多样性与不平衡性，单一模型对于提取液泛数据的特征信息是不足的。首先介绍了岭参数极限学习机（ridge ELM，RELM）及其递推算法（recursive RELM，RRELM）[17]，以更有效用于在线建模。在RRELM基础上，提出了局部递推岭参数极限学习机(local RRELM，LRRELM)的建模方法。LRRELM对每一个预报新样本，应用“相似输入产生相似输出”的原则单独建模，根据样本的信息充分提取液泛数据和填料的特征，实现更准确的预测。

1 RELM及其递推算法

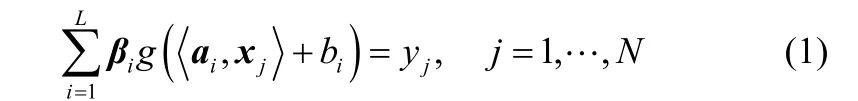
式中，ai为第i个隐层节点与输入节点间的权值；bi为第i个隐层节点的阈值；为ai与xj的内积。

式中，H为隐层输出矩阵；ih是由第i个隐层节点生成的矩阵。此时，非线性系统可通过式（2）转化成一个线性表达式，通过广义逆或最小二乘线性回归算法求解得[9-11]

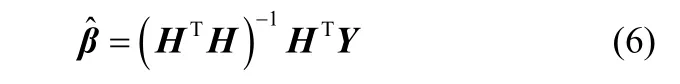
为了避免由于自变量间的复共线性关系而导致病态解问题，可以在式（6）中加入适当的岭参数k，式（6）可进一步表示为

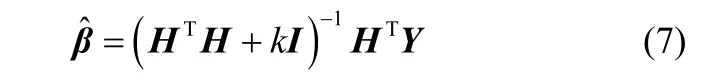
式中，k为岭参数；I为单位矩阵。

式中，Ht是根据测试样本的输入Xt而生成的隐层输出矩阵。

RELM算法的步骤见文献[17]。但传统的RELM 和ELM在获得新节点时，模型都需要重新计算隐层输出矩阵，以获得新的输出权值并重新建立模型。其缺点有：①不断初始化模型可能导致预测的不可靠；②每次都重建模型，计算量相对更多且缺乏效率[17]。因此，需要对RELM进行递推以有效更新模型。

当隐层节点数确定为L，相应的隐层输出矩阵可以表示为

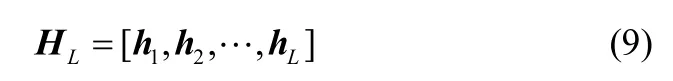
采用RELM进行求解，可获得输出权值

当有新节点加入原模型时，式（9）变为

新节点随机生成的隐层输出矩阵。

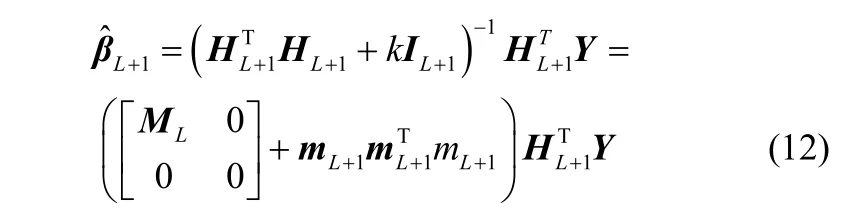
2 局部RRELM建模方法

在实际应用中，要想获得较高的估计精度，需要花费大量的时间选择参数以建立一个全局的模型来描述整个非线性系统。一旦建立了全局模型，当获得的新数据无法反映其中时，模型就需要校正，这也造成了自适应性较差，不能随工况的变动而调整的缺点[18-20]。由于全局建模自身的局限性，为了获得更高的预测精度和可靠的结果，本节将在RRELM基础上进一步改进。

与全局建模不同，局部学习思想采用的是分治的策略，并非对所有样本进行一次性建模，而是针对新样本单独建模，即将系统的非线性整体估计转化成当前状态的点估计。局部建模基于相似输入产生相似输出的原则，模型参数的优化也更为简单，这样可更准确地估计未知样本。模型的建立只有当预报新样本到来时才启动，称为即时学习[18-20]。利用局部学习的思想，提出了LRRELM建模方法，改善了RRELM单一全局模型的缺点。与全局建模相比，对待预报新样本，即时选取关联样本建立模型，这意味着即时学习能实时选择更好的模型，提高预测精度。

局部空间内各样本数据对输出的影响程度各异，根据相似输入产生相似输出的基本原则，可认为局部空间内输入与预报新样本输入向量距离最近的样本的输出值最能反映预报新样本的输出。对于局部建模，由于其模型结构没有任何限制，因此也可采用全局建模中的结构类型。但是局部建模只针对系统的局部特性，并非用于刻画整体系统的输入输出关系。在建模前，首先构建与预报新样本相似的新样本集。同时考虑了样本间的距离和角度信息，以加权的形式将两项信息进行集成[18-20]。获得待预测数据与样本集数据间的相似程度，进行降序排列，选择相似的样本作为建模的样本集[19]。

在建立LRRELM模型时，需要设定隐层节点数，传统ELM初始的节点数通常采用反复的实验获得[9-11]，过程较为繁琐。此处采用留一（leaveone-out，LOO）交叉验证预报误差最小来自动获得节点数。LOO预报误差的表达式如下[16]

所提出的LRRELM方法，用于填料塔液泛气速的在线建模与预测主要步骤如图1所示。RRELM通过递推提高计算效率，并避免了RELM模型不断初始化带来的预测可靠性问题[17]。LRRELM融合即时学习的建模方式，选择更好的局部模型，能针对有差异的填料数据进行更好的建模和预测。

图1 LRRELM用于填料塔液泛气速预测的在线建模流程Fig.1 Flowchart of LRRELM online modeling method for flooding velocity prediction in packed towers

3 实验结果与讨论

3.1 填料塔液泛实验数据

通常情况下，液泛气速受多种因素的影响，如操作介质的物理性质，填料塔的操作条件以及填料的几何特征和物理性质等。考虑到液泛气速的特点及影响因素[4]，确定6种参数作为模型的输入和输出变量。其中，ReL、StL、GaL、SB及φ为输入变量，Lockhart-Martinelli参数（χ）为输出变量，即

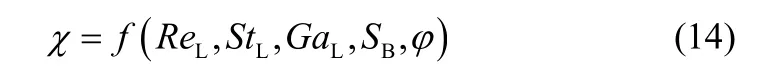
最终，液泛气速UG, Fl可由式（15）得到

本实验共440组填料数据，分布于1976～2007年，源自不同塔径的填料塔，基本覆盖了国内常用的散堆填料[7]。为了使所建液泛预测模型能克服传统经验公式的缺陷，提高其通用性，采用已有的填料数据建模，用于预测缺乏相关数据的新型填料。因此，选择相应的333组训练数据中基本为旧型填料的液泛数据，而剩余107组测试数据中则混合了新型填料与现有填料，以测试所提出方法对新型填料的有效性。

3.2 RRELM与神经网络比较

首先与经典的神经网络比较，以验证RRELM的有效性。采用均方根误差RMSE与平均绝对相对误差AARE衡量预测性能[4]

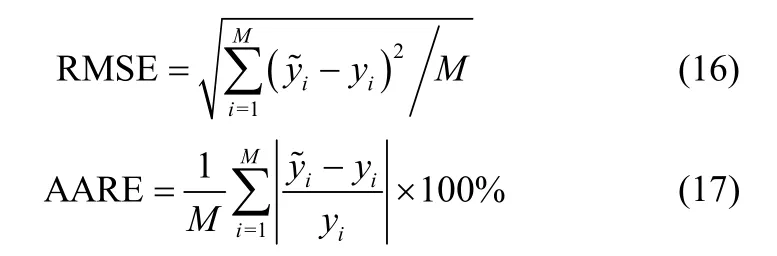
式中，yi为实验值；y~i为预测值；M为测试样本个数。

RRELM与BP-NN[4]、RBF-NN[7]3种模型的预测对比结果如表1、图2和图3所示。由表1可知，RRELM和RBF-NN均比BP-NN模型更准确。

表1 RRELM、BP-NN、RBF-NN 3种模型的预测误差Table 1 Prediction error of three models of RRELM,BP-NN and RBF-NN

图2显示了RRELM、RBF-NN和BP-NN模型的液泛气速预测相对误差比较。从中可知，RRELM除了个别样本相对偏差较大外，其余的样本基本在20%以内，预测效果大都优于BP-NN。图3显示了3种模型的预测值与实验值比较，RRELM大部分分布在0.7～1.2之间，而RBF-NN和BP-NN则分布在0.7～1.4之间。从模型预测的可靠性而言RRELM方法更好，其液泛气速的预测值与真值吻合较好且更均匀分布于其两侧。在工业应用中，可适当加大填料塔的操作气速以提高其生产效率，从而获得更高的经济效益。综上所述，RRELM较BP-NN与RBF-NN预测效果更好。

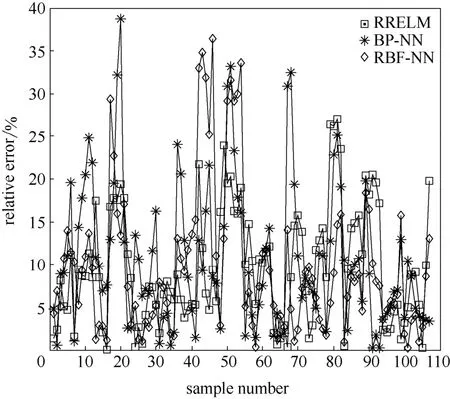
图2 液泛气速预测的3种模型的相对误差对比Fig.2 Comparison of relative prediction error with three models of RRELM, BP-NN and RBF-NN

图3 RRELM、BP-NN和RBF-NN 3种模型预测误差比较Fig.3 Comparison of prediction error with RRELM, BP-NN and RBF-NN models

3.3 LRRELM与RRELM比较

3.2节验证了RRELM模型较传统BP-NN与RBF-NN两种神经网络更适用于液泛气速的预测。本节进一步研究LRRELM模型的预测性能，并和RRELM比较。

RRELM与LRRELM的液泛气速预测结果列于表2。从中可知，LRRELM模型的预测误差（AARE 与RMSE值）较RRELM模型均有降低，主要是因为LRRELM基于相似输入产生相似输出的原则，分析了待预测样本与数据库之间的相关信息，不相关的样本暂不用来建模，选取的相似样本集更符合待预测样本的信息；并在建立模型时进行了节点的优化，以实时建立更可靠的模型，因此综合提高了模型的预测能力。

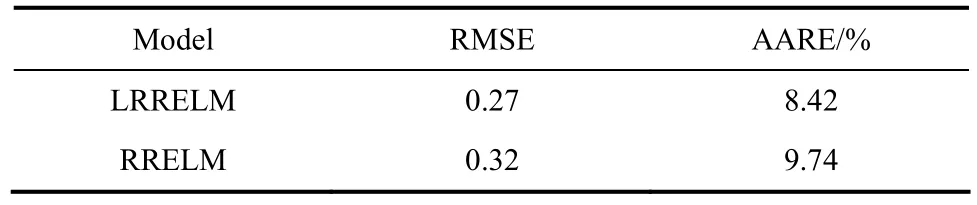
表2 LRRELM和RRELM模型的预测误差对比Table 2 Comparison of prediction error with LRRELM and RRELM models

图4和图5给出了RRELM和LRRELM模型对液泛气速预测值与实验值的比较，其中两者的预测值与实验值变化趋势基本一致，且预测值均匀分布在实验值的两侧。对于大部分样本，LRRELM的预测值与实验值吻合更好、分布更均匀，多数样本预测误差在15%以内。建模过程中，LRRELM会根据每个新预报数据选择所需要的相似样本，结合实际情况，确定最小的样本数为100。从图4可以看出，LRRELM模型需要的样本仅为100～160之间，少于RRELM全局建模方法所需的333组数据，简化了模型的结构。

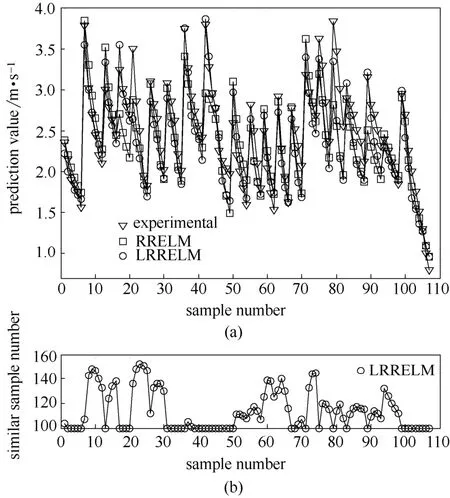
图4 LRRELM和RRELM模型的液泛气速预测值对比（a）及其LRRELM相似样本数量选择（b）Fig.4 Comparison of prediction results with LRRELM and RRELM models (a), and number of similar samples for LRRELM (b)

图5 LRRELM和RRELM的液泛气速预测误差对比Fig.5 Comparison of prediction error with LRRELM and RRELM models

实验测试中，填料类型包括典型的鲍尔环和3种相对新型的填料（环矩鞍、聚乙烯扁环和TGJ2）。针对大部分填料液泛气速的预测，LRRELM最大的相对误差从20%缩减到15%以下，为实际操作气速的选取提供了更大的弹性空间。综上所述，针对液泛气速预测的实验，LRRELM较RRELM效果更优。

4 结 论

针对填料塔液泛气速的预测，全局建模方法建立的模型无法很好满足实际填料的多样性和差异性。基于局部建模的思想，提出了一种LRRELM在线建模方法。通过实验验证，LRRELM较RRELM能获得更佳的预测性能。因此，LRRELM更适用于多类型填料液泛气速的建模和预测。

符 号 说 明

GaL——液相Galileo数

ReL——液相Reynolds数

SB——填料层厚度校正系数

StL——液相Stocks数

UG,Fl——液泛气速，m·s−1

UL——液相表观气速，m·s−1

φ ——填料球形度

ρ ——密度，kg·m−3

下角标

G ——气相

L ——液相

References

[1] PIHLAJA R K, MILLER J P. Detection of distillation column flooding: US 20090314623 [P]. 2009-06-17.

[2] 方向晨, 程振民, 穆斌, 等. 以填料结构为模型参数的填料塔泛点预测新方法 [J]. 华东理工大学学报（自然科学版）, 2006, 32 (4): 370-373. DOI: 10.3969/j.issn.1006-3080.2006.04.002.

FANG X C, CHENG Z M, MU B, et al. New method in prediction of flooding point in packed columns by incorporating packing structure as a model parameter [J]. Journal of East China University of Science and Technology (Natural Science Edition), 2006, 32 (4): 370-373. DOI: 10.3969/j.issn.1006-3080.2006.04.002.

[3] MACKOWIAK J. Fluid Dynamics of Packed Columns [M]. Berlin: Springer, 2009.

[4] PICHE S, LARACHI F, GRANDJEAN B P A. Flooding capacity in packed towers: database, correlations, and analysis [J]. Industrial and Engineering Chemistry Research, 2001, 40 (1): 476-487. DOI: 10.1021/ie000486s.

[5] BRUNAZZI E, MACIAS-SALINAS R, VIVA A. Calculation procedure for flooding in packed columns using a channel model [J]. Chemical Engineering Communications, 2009, 196 (3): 330-341. DOI: 10.1080/00986440802359402.

[6] ENGEL V, STICHLMAIR J, GEIPEL W. Fluid dynamics of packings for gas-liquid contactors [J]. Chemical Engineering and Technology, 2001, 24 (5): 459-462. DOI: 10.1002/1521-4125(200105)24:5＜459:: AID-CEAT459＞3.0.CO;2-D.

[7] 杨捷. 数据驱动的填料塔液泛气速预测模型与实时监测研究[D].杭州: 浙江工业大学, 2011.

YANG J. Research on data-driven prediction model of flooding gas velocity and realtime flooding monitoring in packed column [D]. Hangzhou: Zhejiang University of Technology, 2011.

[8] KADLEC P, GABRYS B, STRANDT S. Data-driven soft sensors in the process industry [J]. Computers and Chemical Engineering, 2009, 33 (4): 795-814. DOI: 10.1016/j.compchemeng.2008.12.012.

[9] HUANG G B, ZHU Y, SIEW C K. Extreme learning machine: theory and applications [J]. Neurocomputing, 2006, 70: 489-501. DOI: 10.1016/j.neucom.2005.12.126.

[10] HUANG G B, WANG D H, LAN Y. Extreme learning machines: a survey [J]. International Journal of Machine Learning and Cybernetics, 2011, 2: 107-122. DOI: 10.1007/s13042-011-0019-y.

[11] FENG G, HUANG G B, LIN Q P. Error minimized extreme learning machine with growth of hidden nodes and incremental learning [J]. IEEE Transactions on Neural Networks, 2009, 20 (8): 1352-1356. DOI: 10.1109/TNN.2009.2024147.

[12] MICHE Y, SORJAMAA A, BAS P. OP-ELM: optimally pruned extreme learning machine [J]. IEEE Transactions on Neural Networks, 2010, 21 (1): 570-578. DOI: 10.1109/TNN.2009.2036259.

[13] HUANG G B, LI M B, CHEN L. Incremental extreme learning machine with fully complex hidden nodes [J]. Neurocomputing, 2008, 71: 1-7. DOI: 10.1016/j.neucom.2007.07.025.

[14] HUANG G B, ZHOU H M, DING X J. Extreme learning machine for regression and multiclass classification [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2012, 42 (2): 513-529. DOI: 10.1109/TSMCB.2011.2168604.

[15] YU Q, MICHE Y. Regularized extreme learning machine for regression with missing data [J]. Neurocomputing, 2013, 102: 45-51. DOI: 10.1016/j.neucom.2012.02.040.

[16] 刘学艺, 李平, 郜传厚. 极限学习机的快速留一交叉验证算法 [J].上海交通大学学报, 2011, 45 (8): 1140-1145.

LIU X Y, LI P, GAO C H. Fast leave one out cross validation algorithm of extreme learning machine [J]. Journal of Shanghai Jiaotong University, 2011, 45 (8): 1140-1145.

[17] 周丽春, 刘毅, 金福江. 一种非线性系统在线辨识的选择性递推方法 [J]. 化工学报, 2015, 66 (1): 272-277. DOI: 10.11949/j.issn. 0438-1157.20141481.

ZHOU L C, LIU Y, JIN F J. A selection recursive method for online identification of nonlinear systems [J]. CIESC Journal, 2015, 66 (1): 272-277. DOI: 10.11949/j.issn.0438-1157.20141481.

[18] LIU Y, GAO Z L, LI P, WANG H Q. Just-in-time kernel learning with adaptive parameter selection for soft sensor modeling of batch processes [J]. Industrial and Engineering Chemistry Research, 2012, 51 (11): 4313-4327. DOI: 10.1021/ie201650u.

[19] LIU Y, CHEN J H. Integrated soft sensor using just-in-time support vector regression and probabilistic analysis for quality prediction of multi-grade processes [J]. Journal of Process Control, 2013, 23 (6): 793-804. DOI: 10.1016/j.jprocont.2013.03.008.

[20] LIU Y, CHEN T, CHEN J H. Auto-switch Gaussian process regression-based probabilistic soft sensors for industrial multigrade processes with transitions [J]. Industrial and Engineering Chemistry Research, 2015, 54 (18): 5037-5047. DOI: 10.1021/ie504185j.

Received date: 2015-12-24.

Foundation item: supported by the Natural Science Foundation of China (61273069) and the Fundamental Research Funds for the Central Universities (JB-ZR1204).

Just-in-time local modeling for flooding velocity prediction in packed towers

ZHOU Lichun1, JIN Xin2, LIU Yi2, GAO Zengliang2, JIN Fujiang1
(1School of Information Science and Engineering, Huaqiao University, Xiamen 361021, Fujian, China;2Engineering Research Center of Process Equipment and Remanufacturing (Ministry of Education), Zhejiang University of Technology, Hangzhou 310014, Zhejiang, China)

Abstract:Packed towers have been widely used in industrial productions. It is important to accurately predict the flooding velocity of packed towers. In industrial practice, there are many kinds of packings which can show different characteristics. Only using a single global model is still difficult to achieve satisfied prediction results. To overcome the problem, a new local modeling method is proposed to predict the flooding velocity. First, a recursive algorithm of ridge extreme learning machine with nodes growing is formulated, which can update the online model in an efficient manner. Moreover, using the just-in-time learning manner, the local recursive ridge parameter extreme learning machine (LRRELM)-based online modeling method is proposed. The experimental results show that the LRRELM model can explore more related information among data and thus to obtain better and more reliable prediction performance, compared with the related global models.

Key words:nonlinear systems; dynamic modeling; neural networks; recursive algorithm; extreme learning machine; systems engineering

DOI：10.11949/j.issn.0438-1157.20151956

中图分类号：TP 301.6；TQ 02

文献标志码：A

文章编号：0438—1157（2016）03—1070—06

基金项目：国家自然科学基金项目（61273069）；中央高校基本科研业务费专项(JB-ZR1204）。

Corresponding author:Dr. LIU Yi, yliuzju@zjut.edu.cn