基于TGNPE算法的间歇过程故障诊断

赵小强，王涛（兰州理工大学电气工程与信息工程学院，甘肃 兰州 730050）



基于TGNPE算法的间歇过程故障诊断

赵小强，王涛
（兰州理工大学电气工程与信息工程学院，甘肃 兰州 730050）

摘要：间歇过程数据是由批次、变量和时间构成的三维数据，数据内包含了丰富的对过程监控有用的全局和局部结构信息，如何充分提取间歇过程的特征信息是故障诊断的关键。传统方法处理三维数据都是将其展开成二维数据，展开过程必然会导致数据内在结构破坏，并且通常只考虑了数据的全局信息或者只考虑了数据的局部信息，这就不能充分提取过程的有用信息导致诊断效果欠佳。针对以上问题，提出了张量全局-局部邻域保持嵌入（TGNPE）算法，首先用张量分解的方法直接对三维数据进行建模，而不对数据进行展开，这就有效地保存了数据的内部结构，再用邻域保持嵌入算法充分提取数据局部结构信息的同时兼顾数据的全局信息，这就实现了对数据特征信息更加充分地提取，用TGNPE算法检测到故障后用贡献图法诊断出故障变量。通过青霉素发酵过程验证了本文提出的算法对间歇过程数据信息提取更加充分，更利于故障诊断。

关键词：间歇过程；故障诊断；张量分解；全局-局部邻域保持嵌入

2015-12-08收到初稿，2015-12-18收到修改稿。

联系人及第一作者：赵小强（1969—），男，博士研究生，教授。基金项目：国家自然科学基金项目（51265032，61263003）。

引 言

间歇过程由于其生产效率高、高附加值等优点成为一种重要的工业生产方式，对间歇过程的故障检测和诊断也日益受到重视。间歇过程与连续过程最大的区别在于间歇过程所获得的过程数据是由时间、变量和批次构成的三维数据，而连续过程数据只是由时间和变量构成的二维数据。面对间歇过程的过程数据呈三维的特点，大多数的处理方法就是将三维数据展开成二维，再对展开后的二维数据用处理连续过程的方法进行建模[1-6]，这些对数据展开的方法虽然解决了对三维数据的建模分析问题，但是对完整的过程数据进行展开必然会破坏数据的内在结构和导致有用信息的丢失，对过程监控产生不利影响。

近年来张量分解（tensor factorization）在特征提取、人脸识别[7]和数据挖掘等领域得到广泛应用，Hu等[8]将张量分解的方法用来处理间歇过程，为处理间歇过程三维数据提供了新的思路，张量分解的方法并不对三维数据进行二维展开，而是在不展开数据的情况下直接对三维数据进行建模，这样就不会破坏数据的内在结构，使更多对监控有利的信息得以保存。张量分解只是对三维数据的一种处理方法，主要是为了保持间歇过程数据内部结构不被破坏，并不能直接用于过程监控，需要结合其他方法对过程数据进行特征提取用以过程监控。文献[8]中提出的TLPP算法虽然能够较好地保留间歇过程数据的三维特点，但是它是一种局部特征提取算法，忽略了数据的全局特征信息，只考虑了局部信息，全局结构信息的丢失必然会给最终的过程监控带来不利。

过程监控的传统方法[9-12]如主元分析（PCA）、偏最小二乘法（PLS）和独立主元分析（ICA）都是寻求方差最大方向最大程度保持数据全局结构特征，却忽略了数据的局部结构。最近，流形算法越来越多地应用到过程监控中，基于局部的流形算法[13-16]如局部保持投影算法（LPP）、局部切空间排列算法（LTSA）和邻域保持嵌入算法（NPE）等，通过样本点及其近邻数据点重构能够很好地提取样本数据的局部结构信息，但此类方法忽略了数据的全局结构信息。不管是将局部信息还是全局信息丢失，都会导致最终的监控结果发生错误。

针对间歇过程监控中数据二维展开后内在结构被破坏和传统方法不能兼顾数据的局部和全局结构信息等问题，本文提出张量全局-局部邻域保持嵌入算法（TGNPE），通过张量分解来对间歇过程三维数据不展开的情况下直接建模，这样能够避免数据展开而破坏数据内在结构和有用信息的丢失，再通过全局-局部邻域保持嵌入算法，在充分提取数据局部信息的同时兼顾数据的全局信息。

1 NPE算法

邻域保持嵌入（NPE）算法是一种局部流形算法，通过利用样本点及其邻近点来表征原始数据空间的局部结构特征。对于训练样本X，首先利用k近邻法（kNN）选取k个样本点作为近邻点，再通过求解式（1）的最优解来求出每个近邻点的重构系数wij。

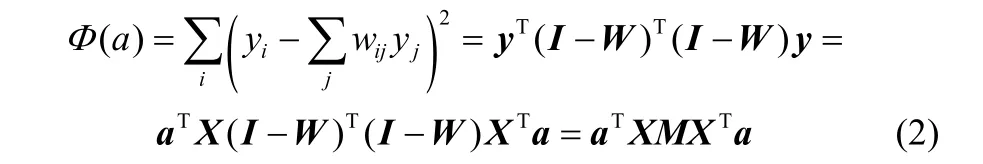
2 全局和局部结构保持

2.1 全局结构保持

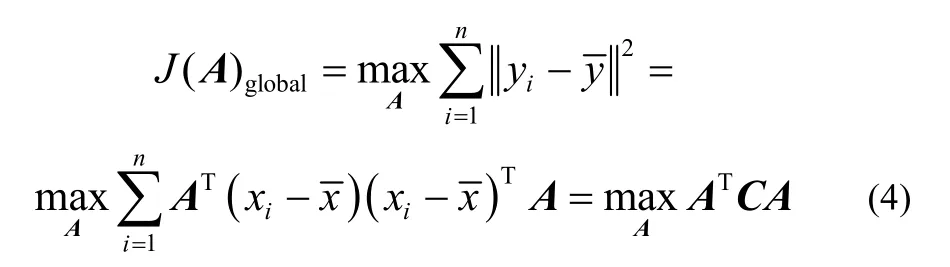
其中

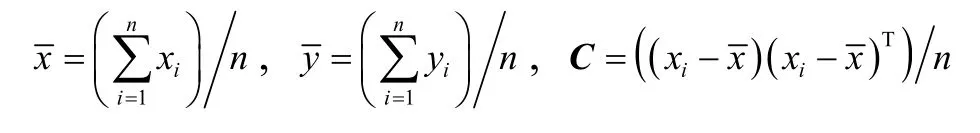
2.2 局部结构保持

局部结构的保持是通过每个数据点及其近邻点进行重构来挖掘出数据局部结构信息，用NPE算法保留局部结构的目标函数见式（5）

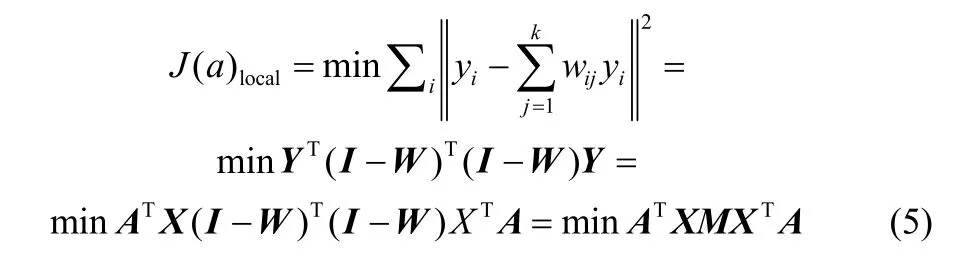
3 基于TGNPE算法的故障诊断

3.1 基于张量分解的全局-局部邻域保持嵌入（TGNPE）算法

对于间歇过程的三维数据的传统处理方法是首先将三维数据展开成二维数据，然后再对展开后的二维数据进行建模，这样强行地将三维数据展开必定会破坏原始数据的内在的结构特征，导致部分有用信息的丢失对过程监控产生不利影响。如果能有一种方法直接对三维数据进行建模，必定能更好地保持数据内部结构，有利于对监控有用信息的提取，张量分解就是一种直接对三维数据进行处理的方法，在不对数据进行二维展开的情况下直接处理三维数据，能够有效地保持数据内部结构的完整。数据信息得到保存并不能对过程监控产生直接作用，必须将数据有用的特征信息充分提取用以过程故障诊断，为了充分提取数据有用的特征信息，本文兼顾数据的全局和局部提出了基于张量分解的全局-局部邻域保持嵌入（TGNPE）算法。

对于批次数为N、变量数为J和时间为K的三维的间歇过程数据矩阵，TGNPE算法就是寻找两个转换矩阵和将X映射到低维特征空间，可得，。

为了能够提取间歇过程的全局结构特征用于过程监控，需要在张量空间找到方差最大方向，通过求解式（6）的最优解来求出相应的变换矩阵U和V

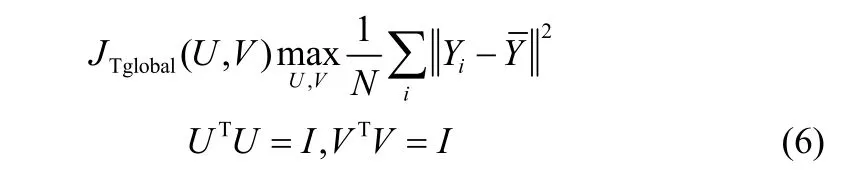
为了能在张量空间中充分提取数据的局部信息，是通过Xi的k个近邻点重构实现的，变换矩阵U和V通过求解式（7）的最优解得到

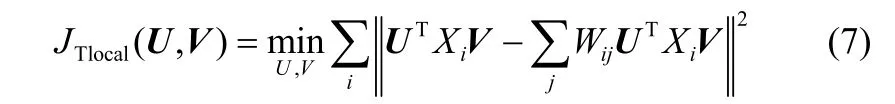
式中，Wij是Xi近邻点的权重系数，具体取值可见文献[8]。

张量分解方法实现了在不对间歇过程数据进行展开的情况下对三维数据进行特征提取，但在张量空间中只考虑全局信息或者只考虑局部信息肯定很难达到对过程数据信息的充分提取，为了更充分地提取间歇过程数据的有用信息，需要在充分保留局部结构信息的同时也能兼顾到数据的全局信息，在张量空间中充分提取数据全局和局部结构信息的目标函数见式（8）

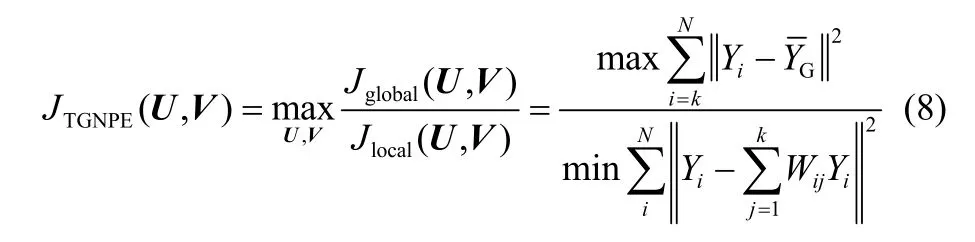
i i

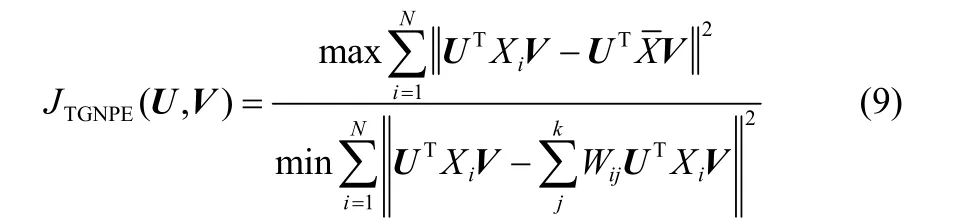
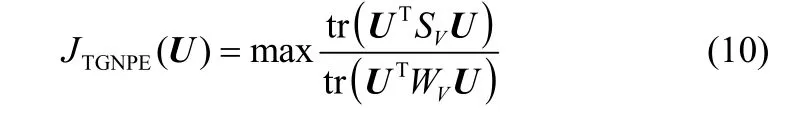
。这样就能够找到U的最优解。将式（9）改写成式（11）

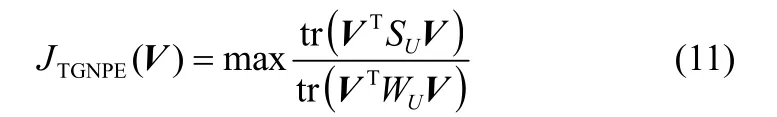
求出了转换矩阵U和V也就能得到低维特征空间Y。

3.2 故障检测与诊断

通过SPE和R2统计量来对过程进行监控。SPE统计量是用来度量样本Xi与特征变量Yi的差异，其具体构造如式（12）

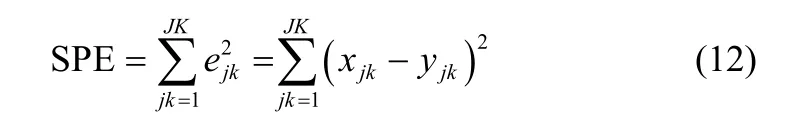
其中，xjk是变量数为j和样本数为k的值，yjk是xjk通过TGNPE算法的投影值。

SPE统计量控制限是由正常工况下的样本的近似2χ分布得到，计算见式（13）

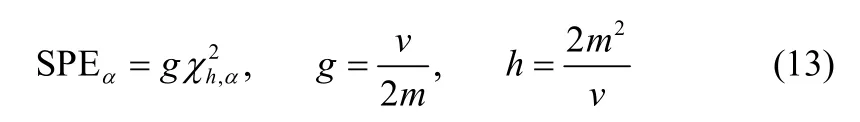
其中，g和h是2χ分布的参数，m和v是训练数据集的均值和方差，α是显著性水平。

R2统计量是新提出的一种过程监控统计量，用每个批次的投影到特征空间中心的距离来度量这个批次的偏离程度，用R2来表示，关于批次Xk的R2统计量的构造见式（14）[18]

R2统计量控制限也是通过样本近似2χ分布估计得到，具体构造见式（15）

其中，m和v是训练数据集中所有的支持张量和离群值的均值和方差。

检测到故障后需要诊断出故障变量，本文采用故障贡献图的方法进行故障诊断，把对故障贡献率最大的变量认为是故障变量。样本时间为j时变量k的SPE统计量的贡献率计算如式（16）所示，R2统计的贡献率ckj计算见式（17）[19]

其中，uk是变换矩阵U的k行，bj是第j个元素为1其他元素都是0的列向量。

3.3 TGNPE算法的监控流程

3.3.1 离线建模步骤

（3）通过构造目标函数式（9）来对张量空间中数据的局部特征信息进行提取的同时兼顾数据的全局特征信息，将原始张量空间映射到低维特征张量空间；

（4）通过求解式（10）和式（11）的最优解得到映射矩阵U和V；

（5）计算出SPE和R2统计量的控制限。3.3.2 在线监控步骤

（1）将在线获得的数据Xnew标准化处理；

（2）将标准化处理后新批次数据作为一个二阶张量空间，通过TGNPE算法将其映射到一个低维的张量空间中得到；

（3）根据式（12）和式（14）计算出在线样本数据的SPE和R2统计量的值；

（4）判断统计量是否超限，若超限说明发生故障，用贡献图法找出故障变量。

4 仿真验证

本文通过Pensim2.0青霉素发酵过程的标准仿真平台产生出间歇过程数据，Pensim2.0是美国Illinois州立理工学院为了更加方便地研究典型间歇过程而开发的[20]，它可产生出不同初始条件和不同工况下青霉素发酵过程中各变量每个时刻的数据用以分析研究。本文将每批次的反应时间设定为400 h，采样时间设为0.1 h，在初始条件设置不同且都在正常范围，不引入故障的情况下共产生50个批次正常工况下数据，从产生的18个变量数据中选择12个过程变量作为监控变量（表1），构成三维矩阵X（50×12×4000）作为训练样本。

表1 过程变量Table 1 Process variable

Pensim2.0仿真平台不仅可以产生正常工况下数据，还提供了3种故障类型，本文中引入故障类型2，即变量2的搅拌功率（agitator power）故障，在采样时间200～400 h（采样点2000～4000）时加入+30%的阶跃信号作为故障信号，所产生的数据作为故障样本以供在线检测。分别用传统的二维展开方法中的多元邻域保持嵌入算法（MNPE）和虽然用张量分解方法来避免三维数据展开但是只考虑局部特征提取忽略了全局信息的张量邻域保持嵌入算法（TNPE）与本文提出的GTNPE算法来对故障样本进行监控，得到图1～图6的监控图。

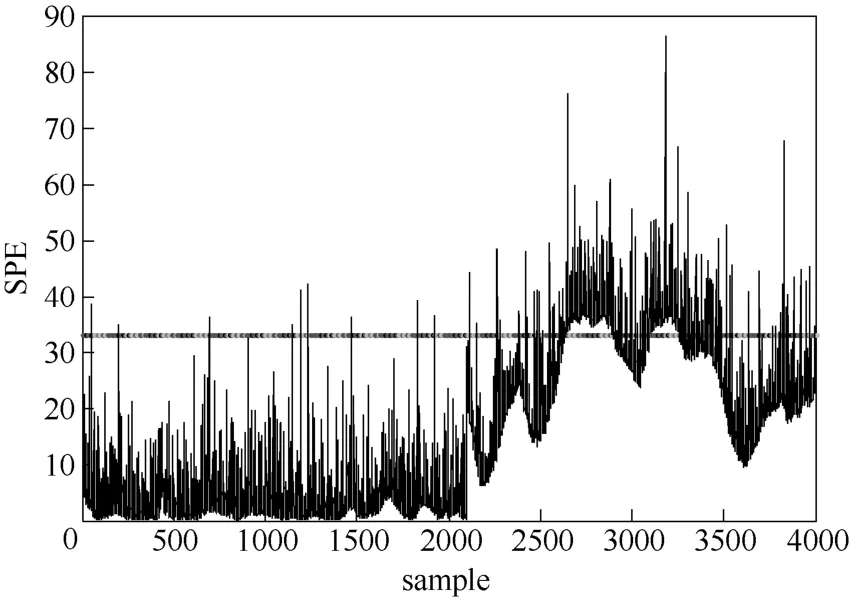
图1 MNPE算法SPE监控图Fig.1 MNPE algorithm SPE monitoring graph

图2 TNPE算法SPE监控图Fig.2 TNPE algorithm SPE monitoring graph

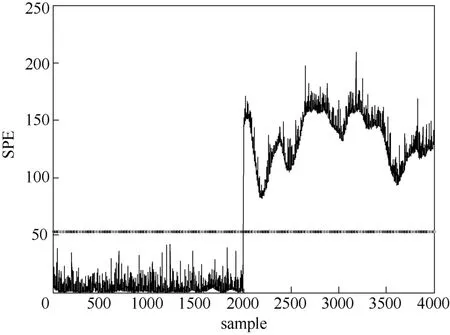
图3 TGNPE算法SPE监控图Fig.3 TGNPE algorithm SPE monitoring graph

图4 MNPE算法T2监控图Fig.4 MNPE algorithm T2monitoring graph

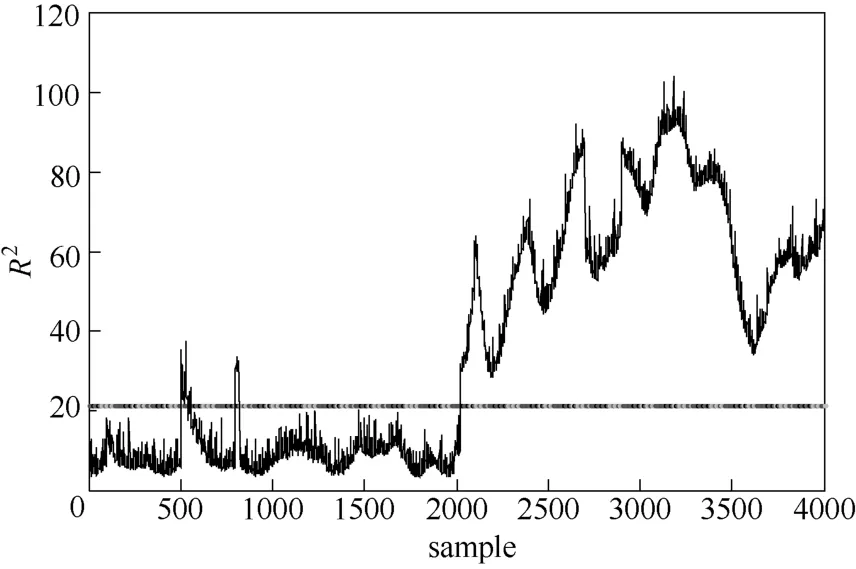
图5 TNPE算法R2监控图Fig.5 TNPE algorithm R2monitoring graph

从图1 的MNPE 算法的SPE监控图可以看出不仅在0～2000采样点之间出现多处误报现象，在200～400 h（采样点2000～4000）引入故障，但是到2500点左右才出现超限，并且之后有相对较多点都在控制线以下，有较严重的漏报现象。所以MNPE方法的SPE统计量监控效果不佳出现较多的误报和漏报，且对故障不敏感有较大的延迟。图2是TNPE算法的SPE监控图，因为采用了张量分解的方法来保存数据的内在结构，用NPE算法来充分提取数据的局部结构信息，能在发生故障的2000点迅速检测到故障并且在2000点后没有在控制限之下的点，说明无漏报现象，但是在无故障情况下出现了若干点超出控制限的情况产生误报现象。图3是本文提出的TGNPE算法的SPE监控图，在无故障的情况下（采样点0～2000）无超出控制限的点，即没有出现误报现象，在刚发生故障的时刻（采样点2000）就能够迅速诊断出故障，在发生故障的2000～4000点，所有点都在控制限之上，无漏报现象。所以从SPE统计量的监控图可得出，用张量分解方法直接处理间歇过程的三维数据比将三维数据展开成二维的处理方法的监控效果要好，在张量分解的基础上兼顾了局部和全局信息的TGNPE算法对间歇过程有较好的监控效果。

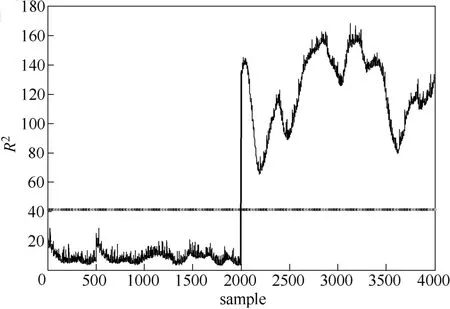
图6 TGNPE算法R2监控图Fig.6 TGNPE algorithm R2monitoring graph

图4是MNPE算法的T2监控图，在采样点550左右和1500点左右都有若干点超出控制限，发生误报，在采样点2000过程发生故障的时刻并不能迅速检测到故障，有几十个采样点的延时，并且在其后又有若干点低于控制限以下发生漏报。图5是TNPE算法的R2监控图，在采样点500点左右和800点左右产生误报，在采样点2030左右才检测到故障，但其后没有点在控制限之下，即没有漏报情况。TNPE 与MNPE算法相比诊断速度更快，漏报现象少，由此可看出用张量分解方法直接处理间歇过程数据比二维展开方法更利于过程监控。图6是TGNPE算法的R2监控图，可以看出在采样点0～2000无任何点超出控制限，说明没有产生误报，在采样点2000时监控图跃升超出控制限，即在刚刚发生故障的200 h时就能迅速检测到故障，在2000点之后的故障点都在控制限之上，即无漏报现象。由此可以看出在用张量分解处理数据的情况下充分考虑局部与全局信息的TGNPE算法对过程监控有较好的监控效果。

检测到过程发生故障后用贡献图法计算出各变量对故障的贡献率，贡献度最大的变量被认为是故障变量。本文选择各种算法的监控图都检测到故障的采样点2700（采样时间为270h）来作各变量的贡献图，诊断结果如图7～图12所示。

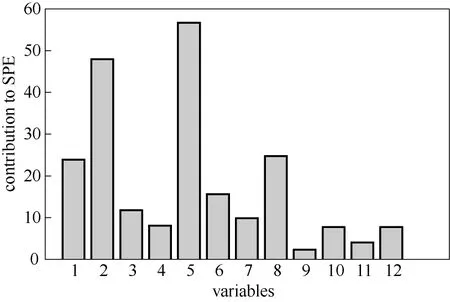
图7 MNPE算法SPE贡献图Fig.7 MNPE algorithm SPE contribution graph

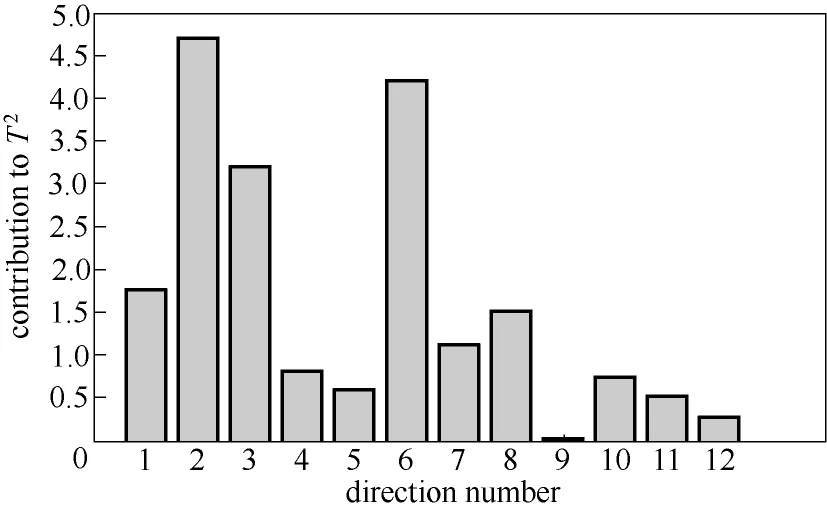
图8 MNPE算法T2贡献图Fig.8 MNPE algorithm T2contribution graph

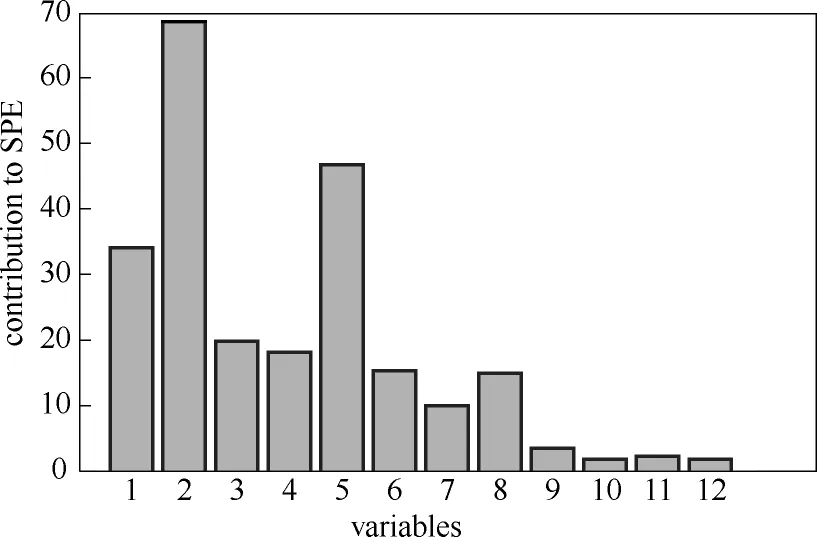
图9 TNPE算法的SPE贡献图Fig.9 TNPE algorithm SPE contribution graph

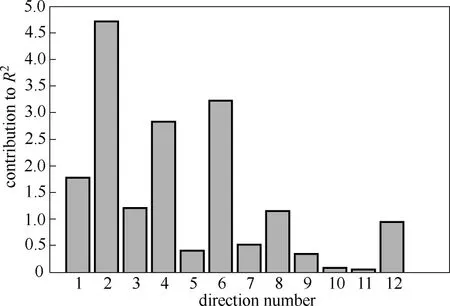
图10 TNPE算法的R2贡献图Fig.10 TNPE algorithm R2contribution graph

图7是MNPE算法的SPE统计量贡献图，图中贡献率最大的变量5并不是真实的故障变量。图8是MNPE算法的T2统计量贡献图，其中贡献率最大的虽然是真实故障变量2，但是变量1、3和6的贡献率也较大。图9和图10是TNPE算法的SPE 和R2统计量的贡献图，两种统计量的贡献图中贡献率最大的都是真实故障变量2，都可以诊断出故障变量，说明张量分解的方法比对数据进行展开的方法诊断效果好，但是SPE的贡献图中变量1和5的贡献率也较大，R2的贡献图中变量1、4和6的贡献率也较大。图11和图12是TGNPE算法的SPE 和R2统计量的贡献图，从图中可以看出只有变量2（实际故障变量）的贡献率较大，其他变量的贡献率都较小，说明TGNPE算法用贡献图法就能准确地诊断出故障变量。

图11 TGNPE算法SPE贡献图Fig.11 TGNPE algorithm SPE contribution figure

图12 TGNPE算法R2贡献图Fig.12 TGNPE algorithm R2contribution figure

5 结 论

间歇过程数据相比连续过程包含着更加丰富的过程信息，不仅包含着各变量和时间之间的关系，而且还包含与批次相关的信息，如何不破坏数据内在结构，充分提取数据间的特征信息是过程监控的关键。本文提出的张量全局-局部邻域保持嵌入算法（TGNPE）能够很好地避免由于数据展开而导致数据结构被破坏，在充分提取了数据的局部特征信息之时兼顾数据的全局特征信息，能够将间歇过程的三维数据包含的信息充分提取用以故障诊断。通过青霉素发酵过程的仿真实验，验证了本文所提出的算法对间歇过程的故障诊断有较好的诊断效果。

References

[1] NOMIKOS P, MACGREGOR J F. Monitoring batch process using multiway principal component analysis [J]. American Institute of Chemical Engineers, 1994, 40 (8): 1361-1375.

[2] 齐咏生, 王普, 高学金, 等. 一种基于改进MPCA的间歇过程监控与故障诊断方法 [J]. 化工学报, 2009, 60 (11): 2838-2846.

QI Y S, WANG P, GAO X J, et al. Batch process monitoring and fault diagnosis based on improved multi-way principal component analysis [J]. CIESC Journal, 2009, 60 (11): 2838-2846.

[3] 陈亚华, 蒋丽英, 郭明, 等. 基于多向Fisher判据分析的间歇过程性能监控 [J]. 吉林大学学报 (信息科学版), 2004, 22 (4): 384-387.

CHEN Y H, JIANG L Y, GUO M, et al. Monitoring batch processes using multiway Fisher discriminant analysis [J]. Journal of Jilin University (Information Science Edition), 2004, 22 (4): 384-387.

[4] MORI J C, YU J. Quality relevant nonlinear batch process performance monitoring using a kernel based multiway non-Gaussian latent subspace projection approach [J]. Journal of Process Control, 2014, 24 (1): 57-71.

[5] STUBBS S, ZHANG J, MORRIS J L. Multiway interval partial least squares for batch process performance monitoring [J]. Industrial and Engineering Chemistry Research, 2014, 52 (35): 12399-12407.

[6] 赵春晖, 王福利, 姚远, 等. 基于时段的间歇过程统计建模、在线监测及质量预报 [J]. 自动化学报, 2010, 36 (3): 366-374.

ZHAO C H, WANG F L, YAO Y, et al. Phase-based statistical modeling, online monitoring and quality prediction for batch processes [J]. Acta Automatica Sinica, 2010, 36 (3): 366-374.

[7] LIU S, RUAN Q Q. Orthogonal tensor neighborhood preserving embedding for facial expression recognition [J]. Pattern Recognition, 2010, 44 (7): 1497-1513.

[8] HU K L, YUAN J Q. Batch process monitoring with tensor factorization [J]. Journal of Process Control, 2009, 19 (2): 288-296.

[9] 肖应旺, 徐保国. 改进PCA在发酵过程监测与故障诊断中的应用[J]. 控制与决策, 2005, 20 (5): 571-574.

XIAO Y W, XU B G. Application of improved PCA to fermentation process monitoring and fault diagnosis [J]. Control and Decision, 2005, 20 (5): 571-574.

[10] ZHOU D H, LI G, QIN S J. Total projection to latent structures for process monitoring [J]. AIChE Journal, 2010, 56 (1): 168-178.

[11] 王丽, 侍洪波. 基于核独立元分析的间歇过程在线监控 [J]. 化工学报, 2010, 61 (5): 1183-1189.

WANG L, SHI H B. Online batch process monitoring based on kernel ICA [J]. CIESC Journal, 2010, 61 (5): 1183-1189.

[12] LOUWERSE D J, SMILDE A K. Multivariate statistical process control of batch processes based on three-way models [J]. Chemical Engineering Science, 2000, 55 (7): 1225-1235.

[13] DENG X G, TIAN X M. Sparse kernel locality preserving projection and its application in nonlinear process fault detection [J]. Chinese Journal of Chemical Engineering, 2013, 21 (2): 163-170.

[14] HU K L, YUAN J Q. Multivariate statistical process control based on multiway locality preserving projections [J]. Journal of Process Control, 2008, 18 (7/8): 797-807.

[15] 张少捷, 王振雷, 钱锋. 基于LTSA的FS-SVDD方法及其在化工过程监控中的应用 [J]. 化工学报, 2010, 61 (8): 1894-1900.

ZHANG S J, WANG Z L, QIAN F. FS-VDD based on LTSA and its application to chemical process monitoring [J]. CIESC Journal, 2010, 61 (8): 1894-1900.

[16] 宋冰, 马玉鑫, 方永锋, 等. 基于LSNPE算法的化工过程故障检测 [J]. 化工学报, 2014, 65 (2): 620-627.

SONG B, MA Y X, FANG Y F, et al. Fault detection for chemical process based on LSNPE method [J]. CIESC Journal, 2014, 65 (2): 620-627.

[17] 王健, 冯健, 韩志艳. 基于流形学习的局部保持PCA算法在故障检测中的应用 [J]. 控制与决策, 2013, 28 (5): 683-687.

WANG J, FENG J, HAN Z Y. Locally preserving PCA method based on manifold learning and its application in fault detection [J]. Control and Decision, 2013, 28 (5): 683-687.

[18] LUO L J, BAO S Y, GAO Z L, et al. Batch process monitoring with tensor global-local structure analysis [J]. Industrial & Engineering Chemistry Research, 2013, 52 (50): 18031-18042.

[19] LUO L J, BAO S Y, GAO Z L, et al. Tensor global-local preserving projections for batch process monitoring [J]. Industrial & Engineering Chemistry Research, 2014, 53 (24): 10166-10176.

[20] BIROL G, ÜNDEY C, CINAR A. A modular simulation package for fed-batch fermentation: penicillin production [J]. Computers and Chemical Engineering, 2001, 26 (11): 1553-1565.

研究论文

Received date: 2015-12-08.

Foundation item: supported by the National Natural Science Foundation of China (51265032, 61263003).

Batch process fault diagnosis based on TGNPE algorithm

ZHAO Xiaoqiang, WANG Tao
(College of Electrical Engineering and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, Gansu, China)

Abstract:Batch processes data is three dimensional data composed of lots of the batches, variables and time. The data contains abundant useful global and local structure information for process monitoring. The key of fault diagnosis is to fully extract the feature information of batch process. The traditional methods unfold three-dimensional data to two-dimensional data. The process inevitably leads to destructing internal structure of the data. The traditional methods usually only consider the global information data or local information data, then the useful process information can not be fully extracted, which leads to poor diagnosis. Aiming to above problems, a tensor globallocal neighborhood preserving embedding (TGNPE) algorithm is proposed in this paper. First tensor factorization is used to deal with three-dimensional data directly which effectively save the internal structure of the data. Then the neighborhood preserving embedding algorithm is used to extract the local structure of the data information, at the same time considering the global information of the data. The data information can be fully extracted under keeping internal data structure. The contribution plot method is used to diagnose fault variables after detecting faults. The simulation results of penicillin fermentation process verified the effectiveness of the proposed algorithm.

Key words:batch process; fault diagnosis; tensor factorization; global-local neighborhood preserving embedding

DOI：10.11949/j.issn.0438-1157.20151857

中图分类号：TP 277

文献标志码：A

文章编号：0438—1157（2016）03—1055—08

Corresponding author:Prof. ZHAO Xiaoqiang, xqzhao@.lut.cn