基于KECA的化工过程故障监测新方法

齐咏生，张海利，高学金，王普（内蒙古工业大学电力学院，内蒙古 呼和浩特 0005；北京工业大学电子信息与控制工程学院，北京 004；教育部数字工程研究中心，北京 004）



基于KECA的化工过程故障监测新方法

齐咏生1,3，张海利1，高学金2,3，王普2,3
（1内蒙古工业大学电力学院，内蒙古 呼和浩特 010051；2北京工业大学电子信息与控制工程学院，北京 100124；3教育部数字工程研究中心，北京 100124）

摘要：针对化工过程数据复杂、非线性的特点，提出一种基于核熵成分分析（KECA）的化工过程故障监测算法。首先，KECA算法按照Renyi熵值的大小选取特征值及特征向量，相比传统的KPCA监测算法，其保留主元个数更少，可以有效减少运算量。同时，仿真研究表明KECA算法选取的主元具有角度结构特性，据此，提出一种新的统计量——CS（Cauchy-Schwarz）统计量，其对应到核特征空间中即为向量间的角度余弦值，可以较好表述不同概率密度分布之间的相似度。最后，将KECA和KPCA算法分别应用于TE（Tennessee Eastman）过程，结果表明KECA在故障检测延迟与检出率相比KPCA都有很大的优势。

关键词：安全；过程控制；主元分析；故障监测；KECA；CS统计量

2015-12-14收到初稿，2015-12-16收到修改稿。

联系人及第一作者：齐咏生（1975—），男，博士，副教授。

引 言

化工过程工艺复杂且常伴随高温高压等极端条件，原材料及产品具有易燃易爆、有毒有害等特点，且生产装置呈现大型化和连续化。一旦出现异常或事故就会破坏正常生产过程，不但可能影响生产进度，还有可能危及人们的生命安全，造成巨大的损失。所以，对化工过程进行故障监测研究就显得非常重要[1-4]。近年来，将多元统计分析应用于化工过程监控中，形成了多元统计过程监控（multivariate statistical process monitoring，MSPM）。其基本思想是通过构造一组维数较低的不相关的隐变量来概括高维数据所携带的信息。常见的多元统计过程监控方法有主元分析（principal component analysis，PCA）[5]、偏最小二乘算法（partial least squares，PLS）[6]、独立主元分析（independent component analysis，ICA）[7]以及这些算法的一些改进算法等。

多元统计监控[8]的核心思想是通过数据投影的方法将输入空间划分为特征空间和残差空间达到数据降维的效果，检测平方预测误差（squared prediction error，SPE）、Hotelling T2（T2）等统计量是否超越控制限来判断过程是否发生异常情况。其中，PCA算法应用最为广泛，它可以有效将含噪声且相关的高维数据以保留原始数据的最大方差的原则投影到低维空间。然而，PCA算法的前提是假设数据为线性[9-10]，它对于非线性过程的监控效果并不十分理想。Scholkopf等[11]提出了核主元分析（KPCA），KPCA是通过非线性映射将原输入空间映射到高维特征空间，然后在这个高维特征空间内进行主元分析，从而把输入空间中的非线性问题转化为特征空间中的线性问题[12-13]。

Jenssen[14]在KPCA的基础上提出KECA算法用于数据转换和数据降维，在提取数据特征上表现出了其独特的优越性。KECA算法通过将输入空间投影到KPCA主轴上实现数据的转换和降维，它与KPCA最大的不同是通过对输入空间熵值的贡献大小来选取主元[15]，因此，KECA算法选取的主元不一定对应于核矩阵较大的特征值和特征向量，且结果显示KECA选取的主元具有一定的角度结构，即不同类别数据的主元分别聚集在不同的坐标轴 附近。

本文将KECA算法应用于过程故障监测中，基于KECA选取主元的角度结构，定义了一种新的统计量表达这种角度结构，与KPCA监控算法的SPE统计量和Hotelling T2统计量相比，具有一定的优势。

1 KECA算法

给定N维样本x，p(x)是概率密度函数，则其Renyi熵计算公式为[16]

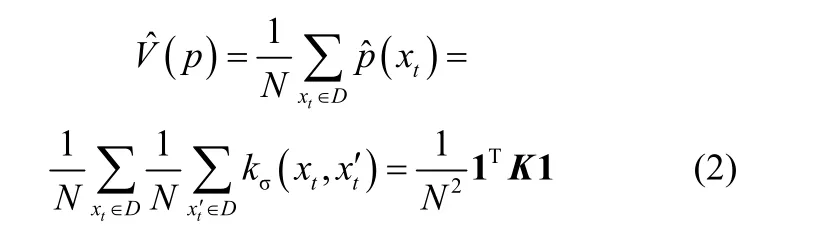
式中，K为N×N的核矩阵；1为元素均为1 的N×1的向量。Renyi熵估计可由核矩阵的特征值和特征向量来表示，将核矩阵进行特征分解D为特征值矩阵D =为特征向量矩阵，计算得到式（3）

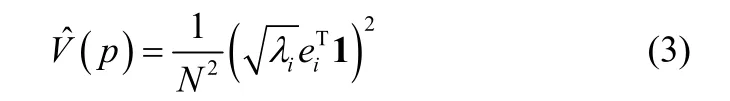
将N维数据通过Ф映射到由k个KPCA主轴张成的子空间Uk上，选取对Renyi熵贡献较大的前k个特征值和特征向量，不一定是特征值较大的前k个，可以得到转换后的数据

样本外数据投影到Uk上的计算公式为

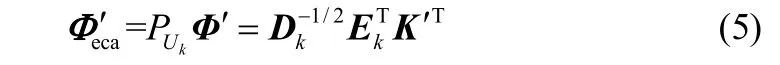
KECA算法可以表述为使核空间数据均值向量的平方欧氏距离与转换后数据均值向量的平方欧氏距离之差尽可能小。为了能够更多保留原始数据的信息，在数据降维时采用熵值贡献率来确定选取主元的个数。

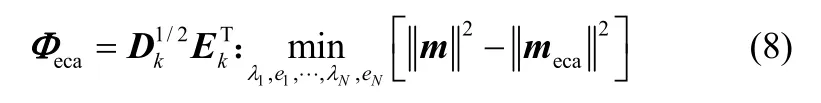
KECA算法实质是一种数据转换方法，它可以最大限度保留核空间数据均值向量的欧氏距离。对TE过程的21种故障均选取3个主元，降维后数据保留原始数据在核特征空间均值向量的比值可达到99%。而KPCA需要选取大约26个主元，其方差贡献率方能达到80%以上。

2 新的监控统计量——CS统计量

CS散度测度衡量两种概率密度函数p1(x)和p2(x)之间的“距离”，表示的是两种概率密度函数之间的相似度[17-18]，计算公式如下其中，0≤DCS＜∞，当且仅当p1(x)= p2(x)时取得最小值。

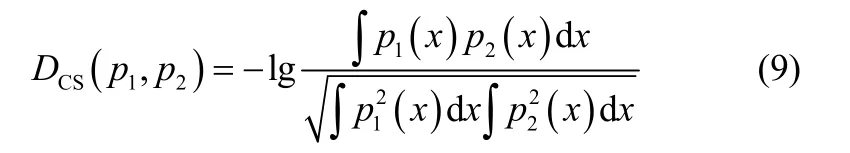
概率密度分布函数之间的CS散度测度可以表示为核空间均值向量之间角度的余弦值[18]。例如，概率密度函数p1( x )和p2( x )之间的CS散度测度为

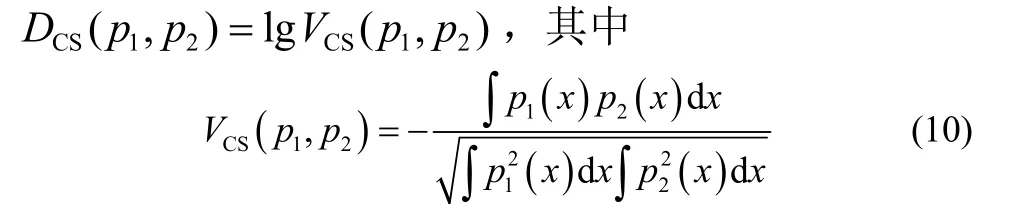
在此，

3 基于KECA的故障监测模型

3.1 建立离线模型

（1）将正常数据与故障数据组成新的建模数据，并对其按正常数据的均值及方差进行标准化

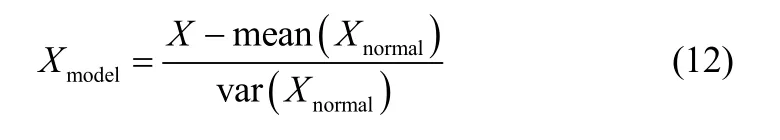
（2）给定核函数(本文采用高斯核)及核参数，利用建模数据进行KECA建模，选取较大熵值对应的特征值及特征向量，对投影后的正常数据求均值m。

需要注意的是，本文需要建立21个模型，每个模型数据由正常数据和一种故障数据组成，因此，不同的模型具有不同的控制限。

3.2 在线监测

（1）将测试数据同样按上述正常数据的均值及方差进行标准化，然后进行核空间映射，计算，计算与m之间的角度余弦值，即CS统计量。

（2）通过判断CS统计量是否超过控制限来确定工业过程是否产生了故障。

4 结果及分析

采用TE过程的数据进行仿真，TE过程共52个变量，21个故障。训练数据及测试数据均包括1组正常数据及21组故障数据。训练数据每隔3 min采样一次，共采样500次计时25 h，采样点个数为500。其中，对于21组故障数据，1 h后引入故障，即故障前20个采样点属于正常数据，仿真只采用剩下的480个故障数据点进行建模，前20个正常数据点不予考虑。因此训练数据共22组，包括1组500× 52的正常数据及21组480×52的故障数据[19-20]。

同样，测试数据中也有1组正常数据和21组故障数据，每隔3 min采样一次，共采样500次计时48 h，采样点个数为960，其中，对于故障数据，8 h后引入故障，即从第161个采样点开始为故障数据点。因此，测试数据包括1组正常数据及21组故障数据，其维数为960×52，其中故障数据维数为800×52[19-20]。

仿真过程选取的核函数为高斯核函数，保留主元个数为3，保留了超过99%的熵值信息，而KPCA保留主元个数约为26，方差贡献率约为80%，在此，分别将KECA及KPCA方法用于故障3、10、15、21，故障监测结果如下，由于T2统计量的故障监测效果不如SPE统计量，故仅选择了SPE统计量与CS统计量进行比较。

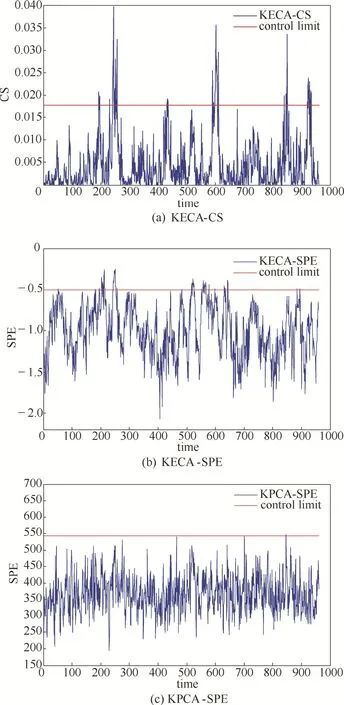
图1 故障3的监测结果Fig.1 Monitoring charts of fault 3 for KECA-CS, KECA-SPE and KPCA-SPE

基于KECA-CS、KECA-SPE[21]及KPCA-SPE方法对故障3的故障监测结果如图1所示。大多故障检测算法都不能够有效地将该故障检测出来，KPCA算法的仿真结果较为混乱，且统计量几乎一直在控制限以下。KPCA-SPE及KECA-SPE算法在整个测试过程，统计量都没有明显的变化，并不能有效地将故障3检测出来，而采用KECA-CS算法，则可以很清楚地看到有两个比较明显的峰值点远远超出了控制限，且正常时刻的统计量没有超限，能够有效地检测出故障3。这是因为KECA在数据特征提取上较KPCA算法有优势，且CS统计量很好地表示了KECA算法所揭露的数据间的角度结构，因此能够有效地将故障数据及正常数据分离开。

图2 故障10的监测结果Fig.2 Monitoring charts of fault 10 for KECA-CS, KECA-SPE and KPCA-SPE

故障10的仿真结果如图2所示。3个图中均有两个比较明显的峰值，其中KPCA-SPE方法仅超过控制限一小部分，而KECA-CS方法超过控制限的部分要远远多于另外两种方法。同时，KECA-CS方法检测出故障的时间也要比另两种提前，即检测延迟少。KECA算法提取正常数据及故障数据间的角度信息，CS统计量将其很好地表示出来，有利于故障监测。因此，KECA-CS方法要优于另两种。

故障15及20的故障监测结果分别如图3、图4所示。对于故障15，KPCA-SPE方法几乎不能检测出故障，KECA-SPE方法则可以明显检测出故障，而KECA-CS不仅能明显检测出故障，时间也远远早于其他方法。KECA算法提取并由CS统计量表示的角度信息提高了故障监测的敏感性。对于故障20，3种方法均能有效检测故障，不同之处在于KECA-CS方法在故障引入120 min处检测出故障，而KPCA-SPE及KECA-SPE方法则在270 min处方能检测出故障，很明显，KECA-CS方法检测故障要提前很多。总之，对于上述几种故障，相比KPCA-SPE及KECA-SPE方法，KECA-CS方法具有更好的故障监测效果。

图3 故障15的监测结果Fig.3 Monitoring charts of fault 15 for KECA-CS, KECA-SPE and KPCA-SPE

图4 故障20的监测结果Fig.4 Monitoring charts of fault 20 for KECA-CS, KECA-SPE and KPCA-SPE

为衡量算法对TE过程的故障监测能力，使用检测延迟（detection latency，DL）[20]、检出率（fault detection rate，FDR）和误报率（false alarm rate，FAR）[21]。其中检测延迟为算法检测出故障的时间与实际故障发生时间的差值，检出率为检出故障数与故障样本总数的比值，误报率误报为故障数与正常样本总数的比值，计算公式如式（13）～式（15）所示。TE过程21种故障的检测延迟、检出率及误报率计算结果见表1，表明了本文算法的有效性。对KECA算法，几乎所有故障的检测延迟都少于KPCA算法，且故障3、4、10、11、15、20故障检出率都明显高于KPCA算法，两种方法的误报率都较低，相差较小。KECA-CS方法在检测工业过程中的微小故障上具有更高的敏感性，TE过程数据的仿真证明了KECA-CS算法在故障实时监测上的可行性及有效性。

表1 TE过程21种故障的检测延迟和故障检出率Table 1 Detection latency (DL) and fault detection rate (FDR) for all 21 faults in TE process

5 结 论

将KECA算法用于TE过程的故障监测。首先，引入Renyi信息熵并以熵值大小选取主元，在数据降维的过程中减少了信息的丢失，既实现了主元选取个数较少，又使降维后数据仍保留了原始数据在核特征空间99%以上的信息熵值。其次，KECA算法选取出的主元具有一定的角度结构，这是在KPCA算法中所没有的。在该角度结构的基础上应用一种新的CS统计量，能够较好表述不同类数据之间概率密度分布的相似度。通过分别将KECA及KPCA算法应用于TE过程对比发现，KECA算法在检测延迟及检出率方面具有较为显著的优势。实验仿真结果表明，基于KECA的过程故障监测算法是行之有效的。

References

[1] 周东华, 李钢, 李元. 数据驱动的工业过程故障诊断技术: 基于主成分分析与偏最小二乘的方法 [M]. 北京: 科学出版社, 2011: 1-9.

ZHOU D H, LI G, LI Y. Industrial Process Fault Diagnosis Technology of Data Driven: Based on Principal Component Analysis and Partial Least Squares Method [M]. Beijing: Science Press, 2011: 1-9.

[2] 马贺贺, 胡益, 侍洪波. 基于马氏距离局部离群因子方法的复杂化工过程故障检测 [J]. 化工学报, 2013, 64 (5): 1674-1682. DOI: 10.3969/j.issn.0438-1157.2013.05.024.

MA H H, HU Y, SHI H B. Fault detection of complex chemical processes using Mahalanobis distance-based local outlier factor [J]. CIESC Journal, 2013, 64(5): 1764-1682. DOI: 10.3969/j.issn.0438-1157.2013.05.024.

[3] 韩敏, 张占奎. 基于改进核主成分分析的故障检测与诊断方法 [J].化工学报, 2015, 66 (6): 2139-2149. DOI: 10.11949/j.issn.0438-1157. 20141378.

HAN M, ZHANG Z K. Fault detection and diagnosis method based on modified kernel principal component analysis [J]. CIESC Journal, 2014, 66(6): 2139-2149. DOI: 10.11949/j.issn.0438-1157.20141378.

[4] 宋冰, 马玉鑫, 方永锋, 等. 基于LSNPE算法的化工过程故障检测 [J]. 化工学报, 2014, 65 (2): 620-627. DOI: 10.3969/j.issn.0438-1157.2014.02.036.

SONG B, MA Y X, FANG Y F, et al. Fault detection for chemical process based on LSNPE method [J]. CIESC Journal, 2014, 65(2): 620-627. DOI: 10.3969/j.issn.0438-1157.2014.02.036.

[5] GARCIA-ALVAREZ D, FUENTE M J, SAINZ G I. Fault detection and isolation in transient states using principal component analysis [J]. Journal of Process Control, 2012, 22(3): 551-563. DOI: 10.1016/j. jprocont.2012.01.007.

[6] YIN S, DING S X, HAGHANI A, et al. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process [J]. Journal of Process Control, 2012, 22(9): 1567-1581. DOI: 10.1016/j.jprocont.2012.06.009.

[7] 徐圆, 刘莹, 朱群雄. 基于多元时滞序列驱动的复杂过程故障预测方法应用研究 [J]. 化工学报, 2013, 64 (12): 4290-4295. DOI: 10.3969/j.issn.0438-1157.2013.12.003.

XU Y, LIU Y, ZHU Q X. A complex process fault prognosis approach based multivariate delayed sequences [J]. CIESC Journal, 2013, 64(12): 4290-4295. DOI: 10.3969/j.issn.0438-1157.2013.12.003.

[8] XIONG L, LIANG J, QIAN J X. Multivariate statistical process monitoring of an industrial polypropylene catalyzer reactor with component analysis and kernel density estimation [J]. Chinese Journal of Chemical Engineering, 2007, 15(4): 524-532. DOI: 10.1016/S1004-9541(07)60119-0.

[9] NOMIKOS P, MACGREGOR J F. Multivariate SPC charts for monitoring batch processes [J]. Technometrics, 1995, 37: 41-59. DOI: 10.2307/1269152.

[10] DONG D, MCAVOY T J. Nonlinear principal component analysis-based on principal curves and neural networks [J]. Computer & Chemical Engineering, 1996, 20(1): 65-78. DOI: 10.1016/0098-1354(95)00003-K.

[11] SCHOLKOPF B, SMOLA A, MULLER K. Nonlinear component analysis as a kernel eigenvalue problem [J]. Neural Computation, 1998, 10: 1299-1319. DOI: 10.1162/089976698300017467.

[12] LEE J M, YOO C K, CHOI S W, et al. Nonlinear process monitoring using kernel principal component analysis [J]. Chemical Engineering Science, 2004, 59: 223-234. DOI:10.1016/j.ces.2003.09.012.

[13] CHO J H, LEE J M, CHOI S W, et al. Fault identification for process monitoring using kernel principal component analysis [J]. Chemical Engineering Science, 2005, 6: 279-288. DOI:10.1016/j.ces.2004.08.007.

[14] JENSSEN R. Kernel entropy component analysis [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(5): 847-860. DOI: 10.1109/TPAMI.2009.100.

[15] JIANG Q C, YAN X F, LÜ Z M, et al. Fault detection in nonlinear chemical processes based on kernel entropy component analysis and angular structure [J]. Korean Journal of Chemical Engineering, 2013, 30(6): 1181-1186. DOI: 10.1007/s11814-013-0034-7.

[16] RENYI A. On Measures of Entropy and Information [C/OL]// Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability. Oakland: University of California Press, 1961, 1: 547-561. http://projecteuclid.org/euclid.bsmsp/1200512181.

[17] JENSSEN R, PRINCIPE J C, ERDOGMUS D. The Cauchy-Schwarz divergence and Parzen windowing: connections to graph theory and Mercer kernel [J]. Journal of the Franklin Institute, 2006, 343(6): 614-629. DOI: 10.1016/j.jfranklin.2006.03.018.

[18] JENSSEN R, ELTOFT T. A new information theoretic analysis of sum-of-squared-error kernel clustering [J]. Neurocomputing, 2008, 72(1/2/3): 23-32. DOI: 10.1016/j.neucom.2008.03.017.

[19] LAU C K , GHOSH K, HUSSAIN M A, et al. Fault diagnosis of Tennessee Eastman process with multi-scale PCA and ANFIS [J]. Chemometrics and Intelligent Laboratory Systems, 2013, 120: 1-14. DOI: 10.1016/j.chemolab.2012.10.005.

[20] MAHADEVAN S, SHAH A L. Fault detection and diagnosis in process data using one-class support vector machines [J]. Journal of Process Control, 2009, 19: 1627-1639. DOI: 10.1016/j.jprocont.2009. 07.011.

[21] YANG Y H, LI X L, LIU X Z, et al. Wavelet kernel entropy component analysis with application to industrial process monitoring [J]. Neurocomputing, 2015, 147: 395-402. DOI: 10.1016/j.neucom. 2014.06.045.

研究论文

Received date: 2015-12-14.

Foundation item: supported by the National Natural Science Foundation of China (61174109, 61364009) and the Natural Science Foundation of Inner Mongolia (2015MS0615).

Novel fault monitoring strategy for chemical process based on KECA

QI Yongsheng1,3, ZHANG Haili1, GAO Xuejin2,3, WANG Pu2,3
(1Institute of Electric Power, Inner Mongolia University of Technology, Hohhot 010051, Inner Mongolia, China;2School of Electric and Information and Control Engineering, Beijing University of Technology, Beijing 100124, China;
3Engineering Research Center of Digital Community, Ministry of Education, Beijing 100124, China)

Abstract:A chemical process fault monitoring algorithms based on kernel entropy component analysis (KECA) is presented for the complexity and nonlinear of industrial chemical process data. The number of principal components selected by the KECA algorism is much less than the KPCA algorism, which can effectively reduce computational complexity. This is achieved by selections onto eigenvalue and eigenvector based on the value of Renyi entropy. Research shows that KECA reveals angular structure relating to the Renyi entropy of the input space data set. A new statistic—Cauchy-Schwarz divergence measure, namely the cosine value between vectors in kernel space, is proposed, which describes the similarity between different PDFs (probability density functions). It is shown that KECA has great advantages in detection latency and fault detection rate in comparing to KPCA by applying them to TE (Tennessee Eastman) process respectively.

Key words:safety; process control; principal component analysis; fault monitoring; KECA; CS statistic

DOI：10.11949/j.issn.0438-1157.20151899

中图分类号：TP 277

文献标志码：A

文章编号：0438—1157（2016）03—1063—07

基金项目：国家自然科学基金项目（61174109，61364009）；内蒙古自治区自然科学基金项目（2015MS0615）。

Corresponding author:QI Yongsheng, qyslyt@163.com