考虑生产成本和环境成本的蒸汽动力系统多目标运行优化

张鹏飞，赵浩，荣冈，冯毅萍(浙江大学智能系统与控制研究所，工业控制技术国家重点实验室，浙江 杭州 310027）



考虑生产成本和环境成本的蒸汽动力系统多目标运行优化

张鹏飞，赵浩，荣冈，冯毅萍
(浙江大学智能系统与控制研究所，工业控制技术国家重点实验室，浙江 杭州 310027）

摘要：石化企业生产过程中污染性气体的排放问题日益引起人们的重视，生产过程进行用能调度运行优化时，需要兼顾节能降本和减少排放两个矛盾的优化目标。综合考虑能源设备、生产操作及大气污染物排放等因素，建立了蒸汽动力系统的多目标混合整数线性规划（MOMILP）模型，采用改进增广ε-约束法对生产成本和环境成本两个目标统筹进行优化，从而获取设备燃料配比和能源分配的优化调度方案。同时，以某石化企业蒸汽动力系统实例为背景，对不同环境收费标准下的生产调度方案进行细致对比和分析，结果验证了所用优化调度模型的有效性。关键词：蒸汽动力系统；公用工程；多目标；优化；环境

2015-05-07收到初稿，2015-09-10收到修改稿。

联系人：荣冈。第一作者：张鹏飞（1991—），男，硕士研究生。基金项目：国家高技术研究发展计划项目（2013AA040701）。

引 言

近年来，能源短缺和环境污染问题日益紧迫，引起了全球范围内的高度关注。石化行业作为典型的高能耗产业，如何通过改进设备和操作工艺来降低生产成本和环境成本，提高综合效益，一直都是该行业的一个重要课题。然而，片面追求生产成本的节约往往会对环境造成严重破坏，而环境友好型生产方式也必然导致生产成本的大幅提升。

石化行业蒸汽动力系统优化调度问题一直是学术界和工程界的研究热点，Papoulias等[1]为对蒸汽动力系统的综合设计进行研究，搭建了MILP模型，Iyer等[2-3]对上述模型进行改进，将其扩展为多周期MILP优化模型。近年来，环境问题日益引起大家的关注，大多数涉及环境因素的蒸汽动力系统优化问题均以上述模型框架为基础，目前常用的研究环境成本的方法主要有两种：一种是建立污染物造成的环境成本与生产成本的多目标优化模型，另一种是将环境成本和生产成本合并为单目标优化问题进行优化。Sayyaadi[4]在设计系统时建立了多目标优化模型，同时考虑到了经济、环境等因素。Francisco等[5]将两种典型大气污染物的排放因素扩充至Iyer等[2]的模型中，并分析了不同的权重系数对于成本的影响。Agha等[6]提出了一个集成优化方法，将产品加工装置与公用工程综合起来进行操作优化，结果表明，这种优化方法大幅节省能源成本，并降低污染性气体的排放。Curti等[7]对集中供热网络建立了环境模型进行优化。但是以上这些研究对污染物种类考虑较少，燃料的选择也较为单一。Luo 等[8]在分析石化企业全厂级蒸汽动力系统的最优化操作计划时，将减排成本和污染物排放成本纳入目标函数，以获得更为全面的优化结果，其对于环境的考虑侧重于CO2收费价格的灵敏度分析。

在多目标优化算法方面，常见的有传统优化算法和智能优化算法两大类。在智能优化算法方面，常用到的算法有NSGA-II和SPEA2等。Mavrotas[9]提出了增广ε-约束法(AUGMECON）避免了冗余迭代从而提高了多目标求解效率。之后对其进行了改进，提出了改进增广ε-约束法(AUGMECON2)[10]。作者将其与SPEA2在背包问题等MOIP优化问题进行了细致比较，从求解时间、精确度方面表明AUGMECON在解决多目标整数规划（MOIP）问题的优势。

本文着眼于炼油企业的实际需求，分析了蒸汽动力系统优化调度的建模框架，并综合原料成本、污染物排放成本和设备操作等成本，建立了蒸汽动力系统的多目标混合整数线性规划（MOMILP）模型，以期得到更为全面的调度方案，优化了设备的燃料配比和能源分配，提高了企业生产操作的经济性和安全性。同时，就相同的生产需求，采用了两种常用的处理环境问题的方法——环境成本和生产成本的多目标优化；环境成本和生产成本合并为单目标优化问题进行优化。考虑到混合整数优化模型特点、复杂度、求解时间及求解效果等因素，引入并实现增广ε-约束法来解决所建立的蒸汽动力系统MOMILP模型。此外，本文考虑了不同的污染物排放标准对于生产调度方案的影响，通过比对优化方案，分析收费标准的变化对于系统优化方案的影响，从而为企业调整生产以应对节能减排要求提供一定的指导。

1 蒸汽动力系统优化调度模型

蒸汽动力系统主要由锅炉、汽轮机、减温减压设备及多种公用工程管网组成。为解决生产计划问题，Micheletto等[11]研究了蒸汽动力系统的总体建模框架，并提出了系统的拓扑结构图，如图1所示。

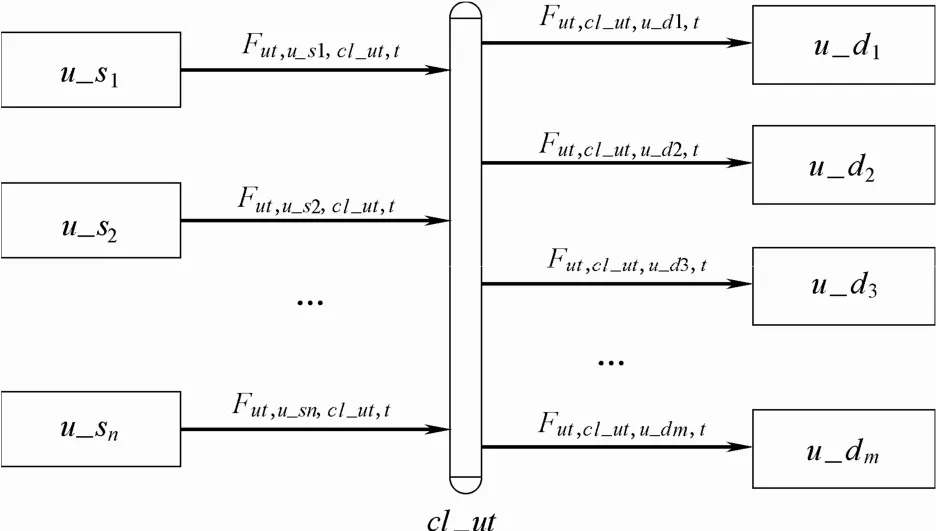
图1 蒸汽动力系统公用工程结构示意图Fig.1 Schematic representation of header of utility cl_ut

在蒸汽动力系统中，每类公用工程都由3部分组成：公用工程生产装置、公用工程输送管线、公用工程消耗装置。在任意调度周期t(t={1,2,…,T})，每种公用工程ut从生产装置u_s传输至相应的集汽联箱cl_ut进行储存，然后统筹分配至每个公用工程消耗装置u_d。通过优化蒸汽动力系统中设备的燃料配比、启停及输出负荷，以实现节能减排的目标。

上述蒸汽动力系统的拓扑结构是建立蒸汽动力系统模型的基础，根据已有的拓扑模型框架，可以从以下5个方面建立蒸汽动力系统优化调度的模型约束。

1.1 通用约束

通用约束主要涉及各周期内设备的物料平衡约束、能量平衡约束以及设备的操作约束等。1.1.1 物料平衡 设备n(n={1,2,…,N})在周期t的所有物料流入量等于所有物料的流出量之和，如式（1）所示，式中n表示蒸汽动力系统中的设备或集汽联箱，i表示流入设备n的第i种物流，j表示流出设备n的第j种物流，F表示其相应流量。

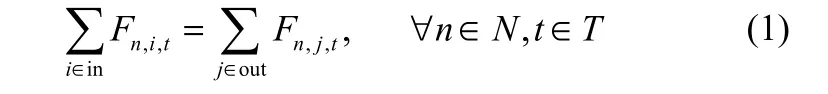
1.1.2 能量平衡 设备n在周期t的所有供给能量之和等于流出能量之和，如式（2）所示。式中H表示周期t流入或流出设备n的物料焓值，Q表示外界提供给装置n的热能。

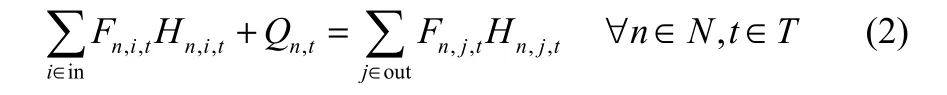
1.1.3 操作约束 设备n在周期t的工作负荷应处于正常范围[式（3）]，式中FL

n,i,t和FU

n,i,t分别指设备n在周期t的负荷下限和上限，Yn,t为0-1变量，用来表征设备是否运行，Yn,t=1则表示设备处于开启状态，反之，则处于关闭状态。在炼厂中，设备的平稳运行对于安全生产至关重要，设备频繁启停一方面会减少设备使用寿命，增加维修成本，另一方面还会影响正常的工作质量，降低炼油企业生产效益，所以需要对设备运行状态的变化进行约束，如式（4）～式（7）所示。

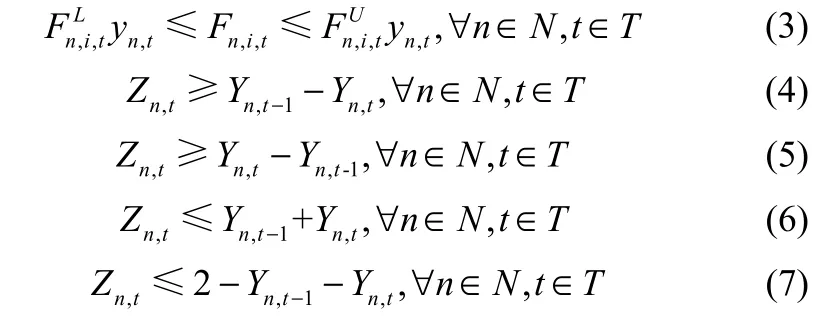
式中，Zn,t用来表征相比于周期t−1(t={2,3,…,T})，设备n在周期t是否发生运行状态的改变。当设备前一周期与本周期的启停状态不一致，则Zn,t为1，反之为0。

1.2 装置约束

1.2.1 锅炉 炼厂锅炉以燃料油或燃料气为燃料，将水加热成高温高压蒸汽，用以满足换热、做功或发电的需要。做功后的蒸汽降级为低压蒸汽汇入低压蒸汽管网。若低压蒸汽产量不足以满足生产要求，除了通过调节透平的抽汽流量外，还可以由高压蒸汽通过减温减压设备降级为低压蒸汽以作补充。从本质上讲，高压蒸汽通过减温减压设备来降级补充是一种能量的浪费，因此在实际的运行优化中，应尽量减少减温减压器的使用。

基于锅炉的热动力学原理，Shang等[12]由锅炉的效率公式推导出锅炉的线性能量模型，较为可靠地反映出锅炉的实际运行状态。根据能量守恒，锅炉燃料的总燃烧热能不仅可以从蒸汽能量结合锅炉工作效率推导得出，如式（8）～式（9）所示，而且可以由燃料的热值计算得出，如式（10）所示，由两式即可得到锅炉的线性模型。

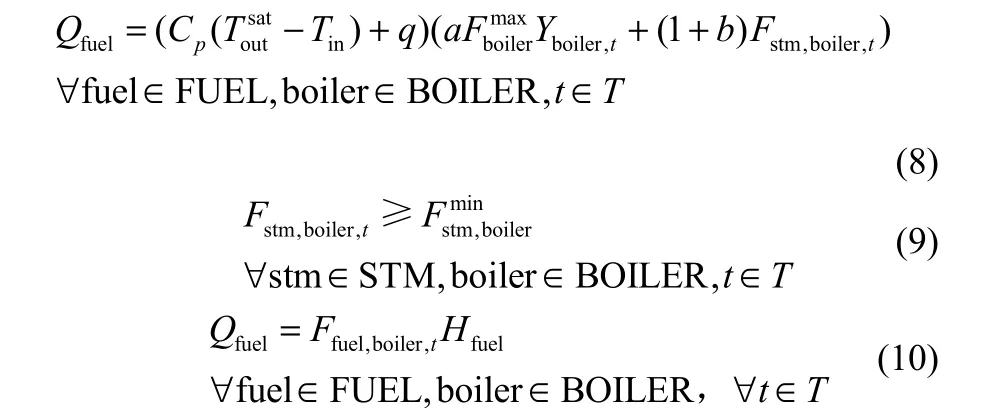
式中，Tin为新鲜水入锅炉时的温度，℃；为蒸汽出锅炉的温度，℃；Cp为饱和水介于Tin和之间的比热，kJ·(kg·℃)−1；q为蒸汽从过热温度到饱和温度的焓变量，kJ·kg−1。式中a和b为锅炉热损失比例和负荷比例回归函数的两个回归参数。表示锅炉boiler的最大蒸汽负荷，t； Fstm,boiler,t为锅炉boiler在周期t的蒸汽流量，t；Ffuel,boiler,t为燃料fuel在周期t的流量(燃料油: t；燃料气: m3)；Hfuel为燃料fuel热值(燃料油: MJ·t−1；燃料气: MJ·m−3)。

1.2.2 汽轮机 汽轮机将蕴含在高温高压蒸汽中的热能转化为机械能或电能。同时，改变汽轮机的抽汽流量也是调节蒸汽管网中不同等级蒸汽平衡的重要手段之一。Shang等[12]改进了背压式汽轮机的数学模型，提高了模型的精度，如式（11）所示。

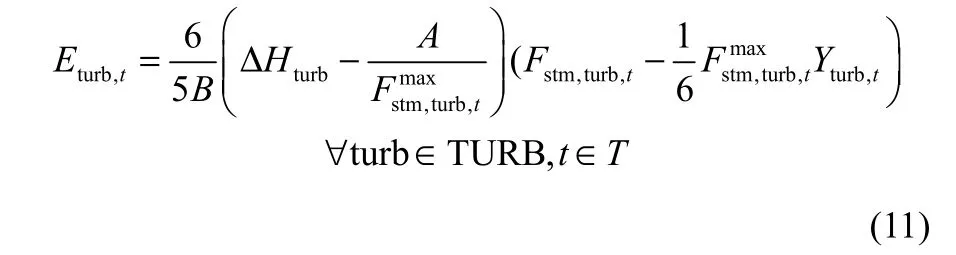
式中，ΔHturb为蒸汽焓降，MJ·t−1；

1.3 供需约束

供需约束主要是满足蒸汽动力系统对蒸汽、动力和电力的需求，其约束分别如式（12）～式（14）所示。在炼厂生产过程中，如果对于外界电网的需求过大，将对电网造成一定的损害，影响电网正常运行，所以需要对外购电力进行约束，如式（15）所示，为系统在周期t从外界电网购入电力的最大值(mWh)。

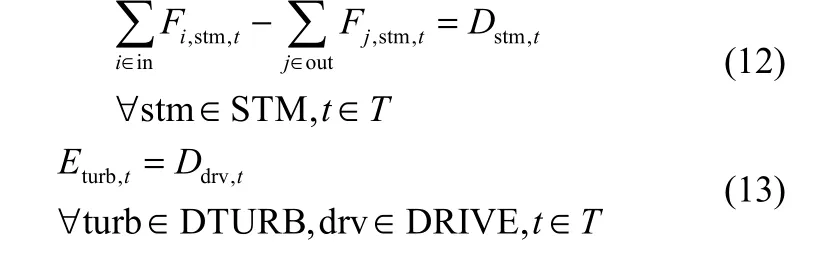
1.4 目标函数

1.4.1 经济-环境多目标优化 蒸汽动力系统能源调度的优化目标是，根据产能和耗能设备的运行参数、能源管网内部不同公用工程的产耗平衡，以及相应污染物的环境指标，建立多目标优化的混合整数线性规划模型，通过模型求解，使得兼顾生产成本和环境成本以满足生产需求。

具体而言，一方面，经济成本，如式（16）所示。包括产能设备燃料成本、新鲜水的成本、外购电力成本以及设备的启停成本。

其中，fuel表示产能设备所用的燃料，如燃料油或者燃料气，Cfuel为燃料的单价，Cwat为新鲜水的单价，Cele为外购电力的单价，Cch_bl表示锅炉设备的启停成本，Cch_tb表示汽轮机设备的启停成本。

另一方面，式（17）所示环境成本包括CO2气体排放成本、SO2气体排放成本与NOx气体排放成本。

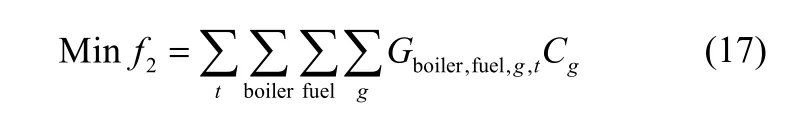
式中，g表示燃料燃烧所排气体，包括CO2、SO2和NOx，Cg表示3种气体排放费用单价。

1.4.2 经济-环境单目标优化 蒸汽动力系统的单目标优化目标是在满足蒸汽、动力和电力需求的前提条件下，优化企业生产操作流程，从而使式（18）所示的总生产成本最低。

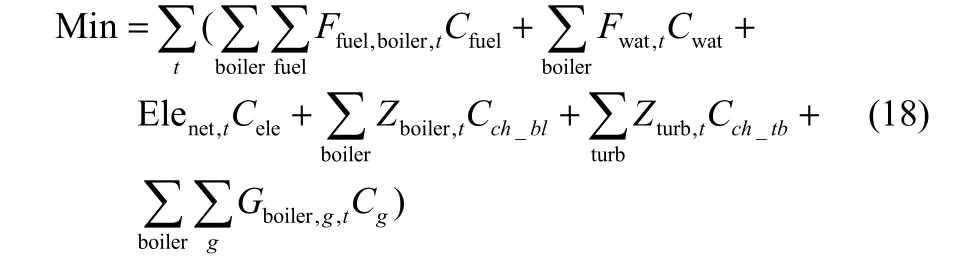
1.5 经济-环境多目标优化模型求解

在经济-环境多目标优化问题中，所考虑的两个目标——节能降本和降低环境成本是冲突和矛盾的，即难以同时满足两者的最优，进而将求解目标转变成获取两个优化目标的折衷方案。求解多目标优化问题的实质便是寻找Pareto最优解的过程，这里所提的最优解只是一种评价解的优劣的标准。

本文采用了改进增广ε-约束法[10]来解决本研究所提到的混合整数多目标优化问题，增广ε-约束法在诸多混合整数多目标优化问题中具有较好的通用性，同时，该引文中将增广ε-约束法与其他多目标求解算法（SPEA2等）从求解时间、每个目标函数的格点数、求解结果准确度等角度说明增广ε-约束法在求解MOIP问题更具实用性和优势。增广ε-约束法目标函数如式（19）所示。

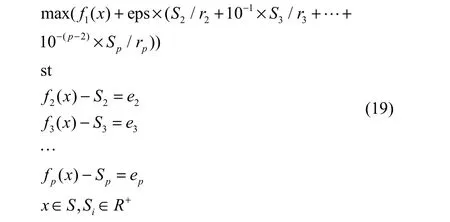
式中，f2(x),f3(x),…,fp(x)为各个优化目标，S为可行域，r2,r3,…,rp为各目标函数的范围，S2,S3,…,Sp是每个约束的剩余变量，e2,e3,…,ep为启发式随机搜索方法中特定迭代的参数。

在该研究实例中，所考虑的两个优化目标的结构和目标表达式如式（16）～式（17）所示。在具体操作时，通过GAMS建模工具将原优化模型与增广ε-约束算法进行集成，同时将优化变量、目标函数和求解算法耦合起来，从而统一优化求解，获取多组Pareto最优解。

2 实 例

该研究实例取自某化工企业的蒸汽动力系统[13]，如图2所示。该蒸汽动力系统包括3种不同等级的蒸汽：高压蒸汽（9.20 MPa，527℃）、中压蒸汽（3.61 MPa，433℃）及低压蒸汽（1.10 MPa，333℃）。整个系统由4台锅炉供应蒸汽，其中1#和2#锅炉用来生产高压蒸汽，且只消耗燃料油。3#和4#锅炉用来提供中压蒸汽，不仅能消耗燃料油，还可以使用燃料气作为燃料。1#、2#和6#、7#为发电汽轮机，驱动发电机为系统提供电能。3#～5#、8#～11#为动力汽轮机，用来驱动动力设备。与此同时，换热过程产生的中低压蒸汽也将汇入蒸汽系统中。该实例所研究的多周期模型总共包含6个连续生产周期，每个周期持续时间为1 h，并主要从生产费用和环境费用两方面进行分析。该案例使用GAMS 24.2.2建立多目标混合整数线性规划模型，并采用CPLEX求解器，计算环境为2.67 GHz Intel(R) Core(TM)2。在两种污染物排放标准下，多目标优化求解时间为33.381 s和29.807 s，单目标优化求解时间为0.542 s 和0.426 s。

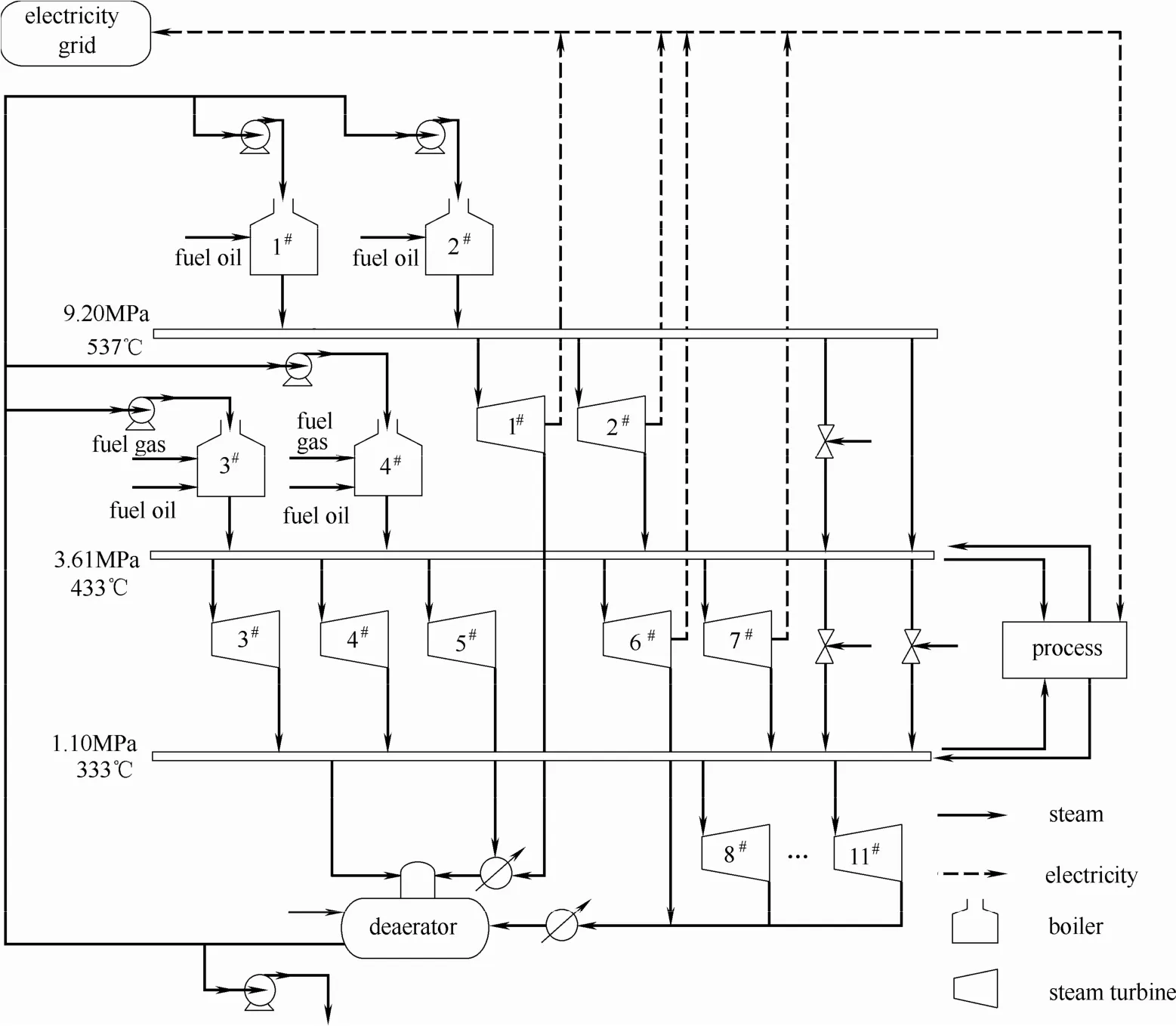
图2 炼厂蒸汽动力系统结构示意图Fig.2 Schematic representation of the utility system in refinery

表1 锅炉参数Table 1 Parameters of boilers

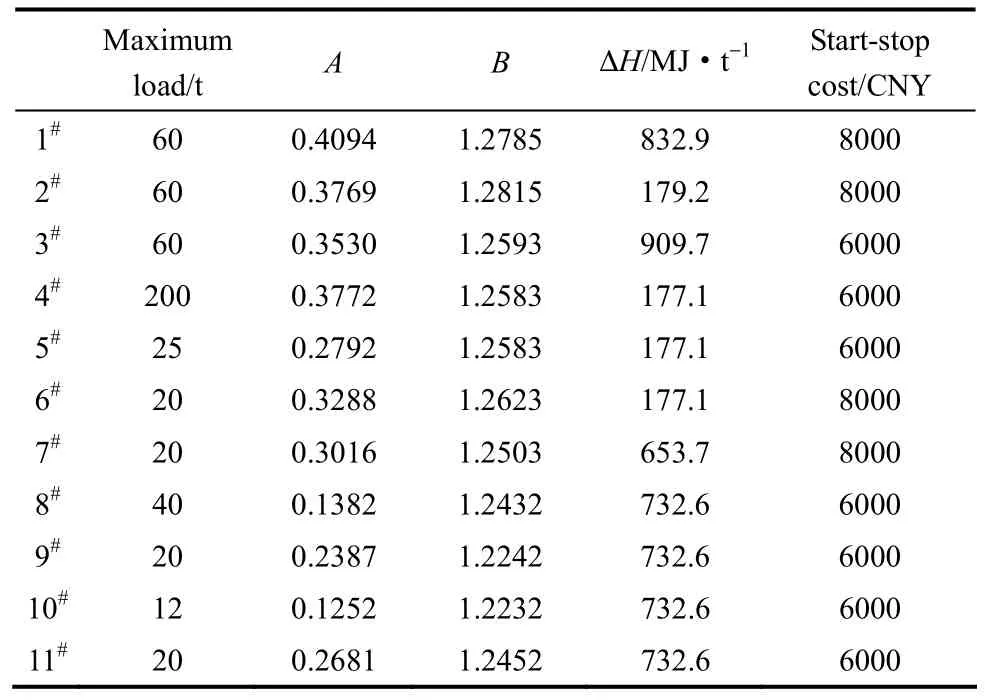
表2 蒸汽轮机参数Table 2 Parameters of turbines

2.1 生产费用

所研究的蒸汽动力系统中，锅炉和汽轮机的参数分别如表1和表2[13]所示，6个周期中蒸汽、动力和电力的产需预测值如表3所示，资源单价如表4所示。

2.2 环境成本

燃料燃烧所排污染物含量与燃料的成分组成直接相关，表5为炼油企业两种常用燃料的相关参数，燃料燃烧产物含量由式（20）～式（22）[14]计算得到，rat表示相应的元素含量比率。

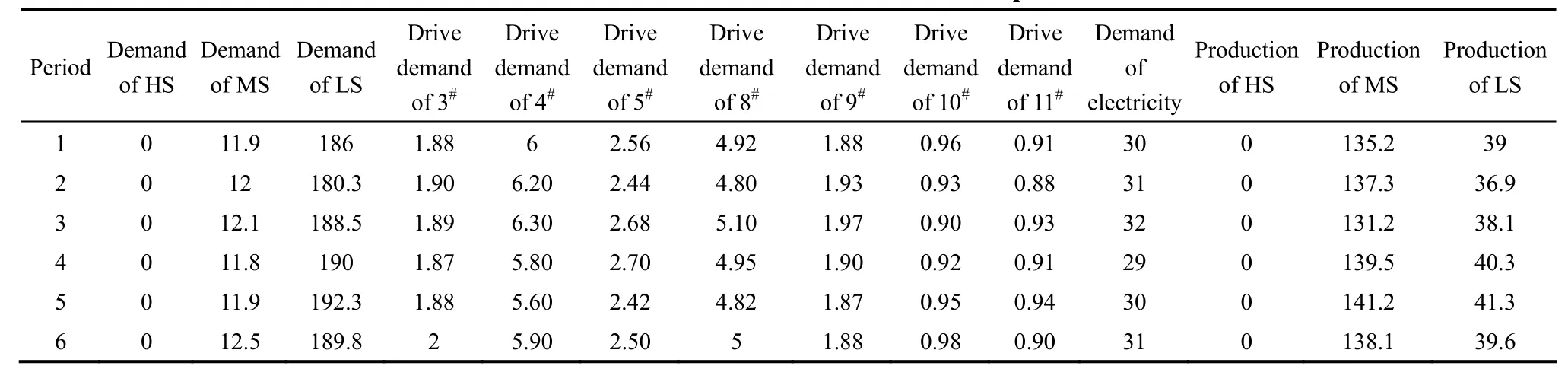
表3 6个周期生产供需预测值Table 3 Possible value of demand in each period

表4 资源单价Table 4 Unit price of resources

表5 燃料参数Table 5 Parameters of fuel in refinery

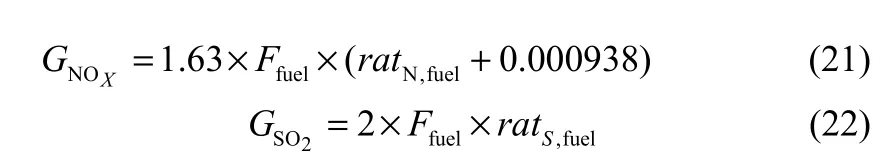
表6 两种环境收费标准Table 6 Two kinds of pollution charge standard/CNY·t−1

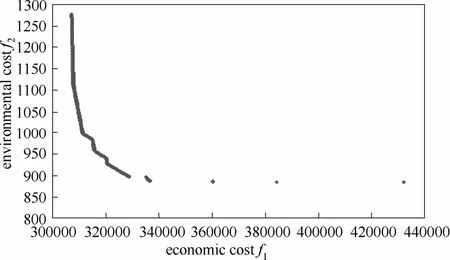
图3 环境标准1对应的生产成本f1-环境成本f2组合Fig.3 Feasible combination of f1and f2under ES1

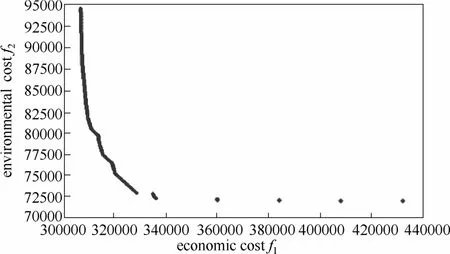
图4 环境标准2对应的生产成本f1-环境成本f2组合Fig.4 Feasible combination of f1and f2under ES2

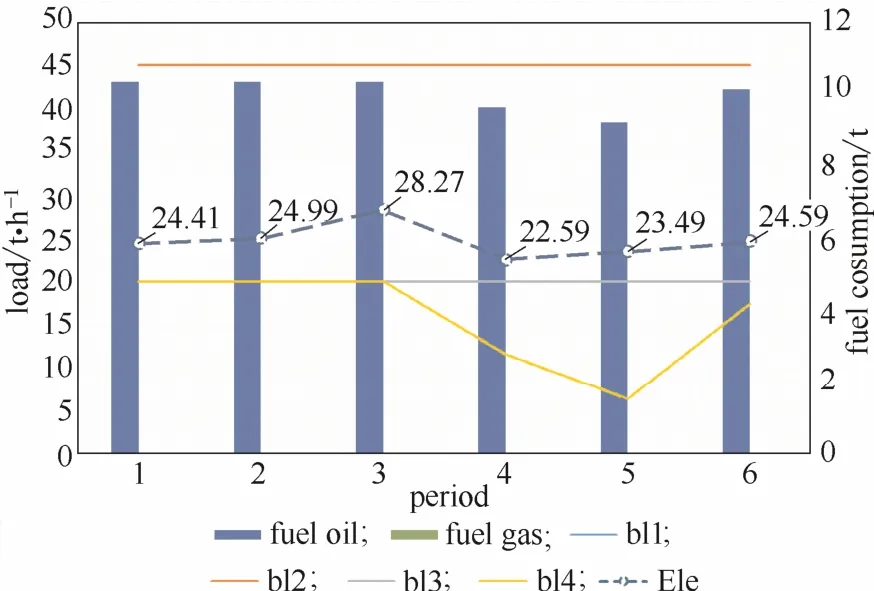
图5 ES1收费标准下的设备负荷和燃料消耗Fig.5 Load of equipment and fuel consumption under ES1

图6 ES1收费标准下的污染物排放Fig.6 Pollution emissions under ES1

目前，业内有两种较为典型的收费标准[8]，如表6所示，其中：ES1是基于2003年以来的国内现行污染物收费标准；ES2数据源自外部成本计划，一种为研究空气污染物所造成的环境破坏而发展来的量化外部成本的方法。

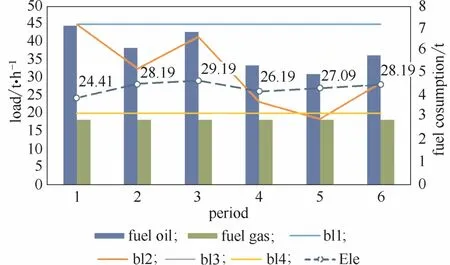
图7 ES2收费标准下的设备负荷和燃料消耗Fig.7 Load of equipment and fuel consumption under ES2

在该研究实例中，当采用多目标优化策略建模并采用增广ε-约束法求解时，两种排放标准下所获得的492组可行解中，生产成本和环境成本的组合

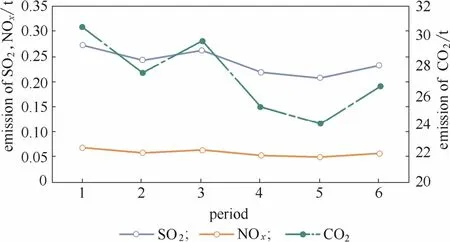
图8 ES2收费标准下的污染物排放Fig.8 Pollution emissions under ES2

散点图分别如图3和图4所示，每一组可行解均有相应的调度优化方案，其中横坐标为生产成本f1，纵坐标为环境成本f2。

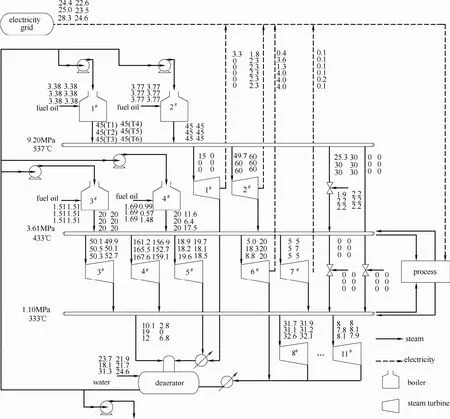
图9 ES1收费标准下的调度方案Fig.9 Scheduling scheme under ES1

进一步地，具体分析图3和图4中满足min(f1+f2)最小的操作策略，即考虑经济-环境的单目标优化时，可得优化结果如下：在收费标准ES1的情况下，系统优化调度对应的燃料消耗和设备负荷如图5所示，相应的污染物排放如图6所示，而在收费标准ES2情况下，系统优化调度对应的燃料消耗和设备负荷如图7所示，相应的污染物排放如图8所示。两种标准下对应的调度方案分别如图9和图10所示。两种标准对应的总燃料消耗量及总污染物排放量如表7所示。

表7 两种标准对应的资源消耗及污染物排放量Table 7 Resource consumption and pollution emissions for each standard

2.3 结果讨论

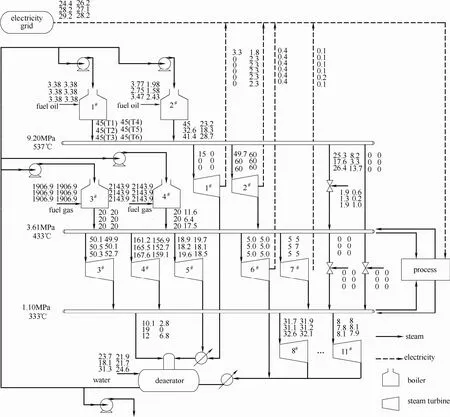
图10 ES2收费标准下的调度方案Fig.10 Scheduling scheme under ES2

从图3和图4分析得到，为降低环境成本以满足环境要求时，生产成本将不可避免地升高，对应图中的可行解从左侧向右侧移动，燃料类型和设备负荷也随之改变。另一方面，对应到综合成本最低的单目标优化，当收费标准从ES1提高到ES2时，则需要重新对原有的优化调度方案进行调整，才能使生产成本和环境成本最低。比较图5～图8还可得到如下结论：当执行ES2标准时，考虑到燃料燃烧的产物排放费用，燃料油的使用成本要比燃料气高很多，因此以燃料油为燃料的2#锅炉负荷大幅降低，其燃料油消耗量也随之降低，污染物排放量也相应减少。耗燃料气锅炉3#和4#则提高工作负荷，用以补充2#锅炉造成的蒸汽产量缺失。进一步的分析可以得到：环境收费标准的变化，主要对涉及能源的设备（如锅炉、发电汽轮机等）负荷产生较大影响。考虑到周期间能源需求和设备负荷的波动，在考虑蒸汽动力系统运行优化时，应当从整体着眼，避免不必要的设备启停，以免增加设备损耗而提高生产运行成本。

3 结 论

本文在研究炼油企业蒸汽动力系统的多周期优化调度问题时，综合原料费用、设备操作费用及多种大气污染物排放费用等因素，建立了更为完善的炼厂蒸汽动力系统多目标运行优化调度模型，从而兼顾生产成本和环境影响，促进企业生产可持续发展。改进增广ε-约束法求解关于生产成本和环境成本的多目标优化问题，考虑了两个目标的折衷，并获取了492个可行解。同时，单目标优化求解获取了最小的综合成本。通过对不同环境收费标准下调度方案的比对，分析了收费标准的变化对于设备负荷和燃料消耗的影响，重点关注该变化对于污染物排放的影响，从而体现本文对于企业在节能环保趋势下进行生产调整的实用性。

符 号 说 明

BOILER ——锅炉集合

D ——公用工程需求量

DRIVE ——动力设备集合

DTURB ——驱动动力设备的汽轮机集合

Ele ——蒸汽动力系统外购电或发电汽轮机产电量

ETURB ——驱动发电机的汽轮机集合

F ——燃料或蒸汽流量

FUEL ——锅炉燃料集合

G ——气体污染物的排放量

H ——热焓或热值

HS ——高压蒸汽

LS ——低压蒸汽

MS ——中压蒸汽

Q ——外界提供给装置的热能

STM ——不同等级蒸汽集合

TURB ——汽轮机集合

Y ——表示设备是否运行的0-1变量

Z ——表示设备是否发生启停转换的0-1变量

下角标

drv ——动力设备

g ——气体污染物类别

i ——流入设备n的第i种物流

j ——流出设备n的第j种物流

n ——蒸汽动力系统中的设备或集汽联箱

net——外界电网

t——生产周期

ut——公用工程

u_d——消耗公用工程装置

u_s——生产公用工程装置

References

[1] PAPOULIAS S A, GROSSMANN I E. A structural optimization approach in process synthesis(Ⅰ): Utility systems [J]. Computers & Chemical Engineering, 1983, 7(6): 695-706.

[2] IYER R R, GROSSMANN I E. Synthesis and operational planning of utility systems for multiperiod operation [J]. Computers & Chemical Engineering, 1998, 22(7): 979-993.

[3] IYER R R, GROSSMANN I E. Optimal multiperiod operational planning for utility systems [J]. Computers & Chemical Engineering, 1997, 21(8): 787-800.

[4] SAYYAADI H. Multi-objective approach in thermoenvironomic optimization of a benchmark cogeneration system [J]. Applied Energy, 2009, 86(6): 867-879.

[5] FRANCISCO A O, MATOS H A. Multiperiod synthesis and operational planning of utility systems with environmental concerns [J]. Computers & Chemical Engineering, 2004, 28(5): 745-753.

[6] AGHA M H, THERY R, HETREUX G, et al. Integrated production and utility system approach for optimizing industrial unit operations [J]. Energy, 2010, 35(2): 611-627.

[7] CURTI V, VON SPAKOVSKY M R, FAVRAT D. An environomic approach for the modeling and optimization of a district heating network based on centralized and decentralized heat pumps, cogeneration and/or gas furnace. Part I: Methodology [J]. International Journal of Thermal Sciences, 2000, 39(7): 721-730.

[8] LUO X, ZHANG B, CHEN Y, et al. Operational planning optimization of multiple interconnected steam power plants considering environmental costs [J]. Energy, 2012, 37(1): 549-561.

[9] MAVROTAS G. Effective implementation of the ε-constraint method in multi-objective mathematical programming problems [J]. Applied Mathematics and Computation, 2009, 213(2): 455-465.

[10] MAVROTAS G, FLORIOS K. An improved version of the augmented ε-constraint method (AUGMECON2) for finding the exact pareto set in multi-objective integer programming problems [J]. Applied Mathematics and Computation, 2013, 219(18): 9652-9669.

[11] MICHELETTO S R, CARVALHO M C, PINTO J M. Operational optimization of the utility system of an oil refinery [J]. Computers & Chemical Engineering, 2008, 32(1): 170-185.

[12] SHANG Z, KOKOSSIS A. A transhipment model for the optimisation of steam levels of total site utility system for multiperiod operation [J]. Computers & Chemical Engineering, 2004, 28(9): 1673-1688.

[13] 章建栋. 炼油企业瓦斯系统优化调度研究及应用[D]. 杭州: 浙江大学, 2009.

ZHANG J D. Research on optimal scheduling of fuel gas system in refinery and its application[D]. Hangzhou: Zhejiang University, 2009.

[14] ZHANG Q, WEILI T, YUMEI W, et al. External costs from electricity generation of China up to 2030 in energy and abatement scenarios [J]. Energy Policy, 2007, 35(8): 4295-4304.

研究论文

Received date: 2015-05-07.

Foundation item: supported by the National High Technology Research and Development Program of China (2013AA040701).

Multi-objective optimization for steam power system considering production cost and environmental cost

ZHANG Pengfei, ZHAO Hao, RONG Gang, FENG Yiping
(State Key Laboratory of Industrial Control Technology, Institute of Advanced Process Control, Zhejiang University, Hangzhou 310027, Zhejiang, China)

Abstract:Gaseous emissions associated with the utility systems increasingly arouse people's attention in recent years. As a result of the severe environment situation, the design criteria for a modern utility system should not only include economic factors but also consider environmental requirements. A multi-objective mixed-integer linear programming (MOMILP) model for the operational planning of steam power system is demonstrated, which taking in account the different units and fuel selection and also the environmental concerns. The improved augmented ε-constraint method is adopted to solve the multi-objective optimization problem of minimization of economic cost and minimization of environmental effect as its capability of producing the exact Pareto set. One motivation example is introduced to analyze the different environmental charge standards and corresponding optimization schemes of the same refinery. In addition, by the comparison, it’s obvious to find the effectiveness of the proposed MOMILP model.

Key words:steam power system; utility; multi-objective; optimization; environment

DOI:10.11949/j.issn.0438-1157.20150575

中图分类号：TQ 021.8

文献标志码：A

文章编号：0438—1157（2016）03—0715—09

Corresponding author:Prof. RONG Gang, grong@iipc.zju.edu.cn