基于时间差分和局部加权偏最小二乘算法的过程自适应软测量建模

袁小锋，葛志强，宋执环（浙江大学控制科学与工程学院，工业控制技术国家重点实验室，浙江 杭州 310027）



基于时间差分和局部加权偏最小二乘算法的过程自适应软测量建模

袁小锋，葛志强，宋执环
（浙江大学控制科学与工程学院，工业控制技术国家重点实验室，浙江 杭州 310027）

摘要：工业过程软测量模型常常因为过程的变量漂移、非线性和时变等问题而使得预测性能下降。因此，时间差分已被应用于解决过程变量漂移问题。但是，时间差分框架下的全局模型往往不能很好地描述过程非线性和时变等特性。为此，提出了一种融合时间差分模型和局部加权偏最小二乘算法的自适应软测量建模方法。时间差分模型可以大大减少过程变量漂移的影响，而局部加权偏最小二乘算法作为一种即时学习方法，可以有效解决过程非线性和时变问题。该方法的有效性在数值例子和工业过程实例中得到了有效验证。

关键词：时间差分模型；局部加权偏最小二乘算法；即时学习；软测量建模；质量预测

2015-12-21收到初稿，2015-12-27收到修改稿。

联系人：宋执环。第一作者：袁小锋（1988—），男，博士研究生。基金项目：国家自然科学基金项目（61370029）。

引 言

在工业过程中，软测量模型被广泛地用于预测过程中因为恶劣测量环境、昂贵的测量仪器和大时间滞后等因素导致难以在线测量的关键过程变量[1-4]。目前为止，大量的软测量方法，如主成分回归(PCA)[5]、偏最小二乘回归(PLS)[6]、人工神经网络(ANN)[7]和支持向量机(SVM)[8]等已经成功地应用于化学、生物、冶金和制药过程等领域[9-11]。

但是，当软测量模型投入实际应用后，其预测性能往往会随着过程状态变化、催化剂活性下降、原材料变化和仪表漂移等因素而慢慢降低[12]。因此，软测量模型需要不断地进行更新。研究学者已经提出一些不同的更新策略，比如递归模型(RM)[13]、滑动窗模型(MW)[14]和即时学习模型(JITL)[15]。依据其更新机制，这些模型可以被分为两大类：时间自适应和空间自适应模型。其中，时间自适应模型包括递归模型和滑动窗模型，因为这些方法将最新获取的样本数据用于更新模型。而即时学习模型，如局部加权偏最小二乘算法(LWPLS)[16]，隶属于空间自适应模型，因为其利用历史数据中和查询样本空间最相关的样本来更新模型。

尽管这些方法可以通过自适应策略来解决过程时变等问题，但其仍然无法解决过程中的变量漂移等问题。若过程存在变量漂移，即时学习或者滑动窗模型的预测精度都会大大降低。因此，时间差分(TD)模型[17]已被提出用于解决此问题。相比于传统软测量方法直接在原始输出和输入之间建立回归模型，时间差分模型将回归模型建立在输出和输入的一阶差分量之间。通过建立时间差分软测量模型，过程变量漂移问题可以有效地解决。同时，文献[18]也比较分析了滑动窗模型、即时学习模型和时间差分模型解决过程变量漂移的能力。结果表明，时间差分模型能取得比其他两种方法更好的预测精度。

事实上，工业过程往往会同时存在非线性、时变和变量漂移等问题。同时，时间差分框架下的全局模型，不能有效地描述数据整体分布特征。为了更好地解决这些问题，本文提出了一种基于时间差分模型和偏最小二乘回归算法的自适应软测量建模方法。首先，时间差分模型用于减少变量漂移的影响。然后，偏最小二乘算法用于精确建立局部差分量回归模型。从而过程时变特性和非线性问题都可以有效解决。

1 算法介绍

1.1 时间差分模型（TD）

假设x(t)和y(t)是分别是过程输入和输出在时刻t的采样值。传统软测量建模中，回归算法直接建立在原始输入输出的采样值上。而时间差分模型首先计算输入和输出在相邻采样点之间的一阶差分量。即Δx(t)和Δ y(t)可以分别计算为[17]

然后，即可建立输入输出差分量之间的回归模型

待上述回归模型训练好之后，当一个新的样本x(tnew)到来，其输入的时间差分量可以计算为

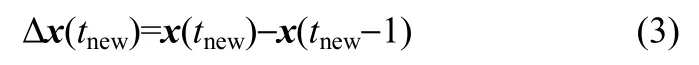
从而，其输出的一阶差分量可通过训练好的回归模型预测为

最终，实际的预测输出值为

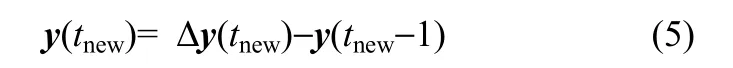
1.2 局部加权偏最小二乘算法（LWPLS）

同时，局部加权偏最小二乘算法还需要依据相似度对各个训练样本给予不同的权重值。因此，以下权重计算公式即可用于指定各样本的权重

其中，θ为控制权重随距离变化快慢的可调节参数。将各个训练样本的权重表示为权重向量w=[w1,w2,…,wN]，而训练样本权重矩阵记为Ω=diag(w)。最后，查询样本的预测输出值可通过以下流程进行估计。

（1）设定第一个隐变量序号k=1和隐变量个数为L。

（2）计算输入和输出的加权平均值，并对训练样本输入、训练样本输出和查询样本输入进行去平均化处理

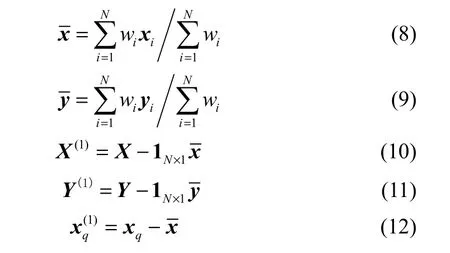
其中，1N×1代表元素值全为1的列向量。

（4）分别计算训练集和查询样本的第k个主成分

其中，v(k)对应于加权输入输出协方差矩阵X(k)TΩY(k)Y(k)TΩX(k)的最大特征值对应的特征向量。

（5）计算X(k)的第k个负载向量和输出的回归系数

（6）利用第k个隐变量更新预测输出值

（8）退化训练输入矩阵、输出矩阵和查询样本输入

（9）设置k=k+1并返回步骤（4）。

2 TD-LWPLS自适应软测量框架

为了克服前文提及的问题，TD-LWPLS自适应软测量建模框架被提出用于非线性时变和变量漂移过程的质量预测。图1给出了该自适应建模框架的基本流程图。

首先，时间差分模型被用于提取输入和输出的一阶差分量，这些差分量被视为历史差分数据库。当一个新的查询样本到达，先计算其输入的时间差分量。然后，在即时学习框架下，可以基于欧式距离准则从历史差分数据库中选择一定数量与查询样本差分量最相关的时间差分量并计算各差分量权重用于局部建模。之后，通过局部加权偏最小二乘算法建立差分量之间的回归模型。最终，计算预测查询样本输出。其详细算法如下。

图1 TD-LWPLS自适应软测量框架流程图Fig.1 Flowchart of TD-LWPLS soft sensor framework

（1）获取历史采样输入数据x(1),x(2),…,x(T+1)和输出数据y(1),y(2),…,y(T+1)。

（2）计算输入输出的差分量Δx(1), Δx(2),…,Δx(T)和Δy(1),Δy(2),…,Δy(T)，并计算查询样本输入的差分量Δx(tq)= x(tq)−x(tq−1)。

（3）通过欧式距离准则计算Δx(tq)和Δx(1), Δx(2),…,Δx(T)中各个差分量距离以及权重值。并选择N个最相关的差分量作为训练集ΔXN和ΔYN，同时获得权重向量w。

（4）通过ΔXN,ΔYN,w和Δx(tq)建立LWPLS模型，预测查询输出的差分量

为验证上述算法有效性，本文比较了一下3种算法的预测性能：

方法1：基于TD模型下的全局PLS模型。

方法2：未加TD模型的LWPLS模型。

方法3：基于TD模型下的LWPLS模型。

3 实验结果与讨论

3.1 数值例子

本数值例子来源于文献[17]，其最初用于验证时间差分模型预测性能。通过以下模型共产生201个数据点。首先，3个隐变量z1, z2和z3均独立地产生于均匀分布[3, 6]。同时，6个正常情况下输入变量由以下方程产生

其中，N(0,0,1)表示均值为0，方差为0.1的正态分布。而输出变量定义为

为了模拟过程变量漂移和时变特性，分别将部分输入或者输出设置为以下4种情形之一。

情形1：只有输入变量存在漂移，即情形2：输入如公式23存在漂移，输出漂移为

情形3：过程无变量漂移，但存在时变特性

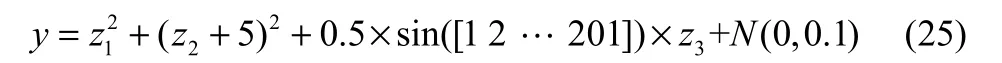
情形4：过程不仅存在输入漂移[式（23）]和输出漂移，同时存在时变特性

为了建模和测试，数据被分成两部分，前101个点作为历史数据集，后100个数据作为测试集。模型参数选择如下：局部建模样本数N为30，隐变量个数为3，参数θ通过试验法优化。最终，均方误差（RMSE）和预测相关系数（R2）用于比较预测精度，结果如表1所示。

由表1可知，在情形1和情形2中，方法1和方法3预测结果明显优于方法2。这是因为此时过程存在变量漂移，而时间差分模型可以有效降低变量漂移的影响，而方法2只用即时学习建模，不能解决变量漂移问题。并且，由于方法3采用了时间差分下的局部加权建模，其比方法1获得了更好的预测精度。在情形3中，由于过程不存在变量漂移，只有特性变化，此时方法2的预测结果要优于方法1和方法3。由此可以看出，即时学习可以有效解决过程时变特性问题。在情形4中，变量漂移和过程特性时变两者同时发生，可以看出此时方法3能够取得最佳的效果。

表1 3种方法在数值例子上的预测结果Table 1 Prediction results of the three methods on numerical example

3.2 高炉炼铁过程

高炉是炼铁过程的重要生产装备[19]，其主要目的是将铁矿石转化为液态铁，其中涉及复杂的物理变化和化学反应。由于炉内高温高压的环境，使得某些变量（如铁水中硅含量）的直接测量变得非常困难。因此，通过软测量方法对该过程的铁水中硅含量进行预测是一种行之有效的方法。本文将16个易测变量选择作为软测量的输入，表2给出了各个输入量的物理含义。

对某高炉平台从2014年1月1日到2014年6 月3日的实际运行数据进行采集，每日采集一个样本。因此，一共采集了154个数据样本。为了软测量建模和性能测试，前101个样本被作为历史数据样本，余下53个样本作为测试集。同时。局部建模样本数选择为30，隐变量个数确定为6。

表2 用于软测量模型输入的高炉过程变量Table 2 Input variables selected for soft sensor on blast furnace ironmaking process

表3 3种方法在高炉炼铁过程中的预测结果Table 3 Prediction results of the three methods on the blast furnace ironmaking process

通过建模和预测，3种方法的模型预测结果列在表3中。由表中可知，TD-LWPLS能够获得最佳的预测效果。因为该方法可以有效减少变量漂移的影响并能够自适应过程特性变化。而方法1由于只是采用了时间差分模型，其难以解决过程时变特性。方法2只利用LWPLS自适应过程特性变化，模型预测性能会受到过程变量漂移的影响。

4 结 论

本文提出了一种TD-LWPLS的自适应软测量建模方法，用于对变量漂移和非线性时变过程的软测量。时间差分模型被用于减少变量漂移对软测量模型的影响。然后，局部加权偏最小二乘算法被用于建立时间差分输入和输出量之间的回归模型，从而处理过程时变和非线性问题。为了验证算法的有效性，预测性能在数值例子和工业过程实例中进行了测试。实验结果表明了所提方法的有效性。

References

[1] KADLEC P, GABRYS B, STRANDT S. Data-driven soft sensors in the process industry [J]. Computers & Chemical Engineering, 2009, 33(4): 795-814.

[2] KHATIBISEPEHR S, HUANG B, KHARE S. Design of inferential sensors in the process industry: a review of Bayesian methods [J]. Journal of Process Control, 2013, 23(10): 1575-1596.

[3] GE, Z Q, SONG Z H, GAO F R. Review of recent research on data-based process monitoring [J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562.

[4] KANO M, NAKAGAWA Y. Data-based process monitoring, process control, and quality improvement: recent developments and applications in steel industry [J]. Computers & Chemical Engineering, 2008, 32(1):12-24.

[5] YUAN X F, YE L J, BAO L, et al. Nonlinear feature extraction for soft sensor modeling based on weighted probabilistic PCA [J]. Chemometrics and Intelligent Laboratory Systems, 2015, 147: 167-175.

[6] ROSIPAL R, KRAMER N. Overview and Recent Advances in Partial Least Squares. In Subspace, Latent Structure and Feature Selection [M]. Berlin Heidelberg: Springer, 2006: 34-51.

[7] RANI A, SINGH V, GUPTA J R P. Development of soft sensor for neural network based control of distillation column [J]. ISA Transactions, 2013, 52(3): 438-449.

[8] YAN W W, SHAO H H, WANG X F. Soft sensing modeling based on support vector machine and Bayesian model selection [J]. Computers & Chemical Engineering, 2004, 28(8): 1489-1498.

[9] GE Z Q, CHEN T, SONG Z H. Quality prediction for polypropylene production process based on CLGPR model [J]. Control Engineering Practice, 2011, 19(5): 423-432.

[10] YUAN X F, GE Z Q, SONG Z H. Locally weighted kernel principal component regression model for soft sensing of nonlinear time-variant processes [J]. Industrial & Engineering Chemistry Research, 2014, 53(35): 13736-13749.

[11] BOSCA S, FISSORE D. Design and validation of an innovative soft-sensor for pharmaceuticals freeze-drying monitoring [J]. Chemical Engineering Science, 2011, 66(21): 5127-5136.

[12] KADLEC P, GRBIC R, GABRYS B. Review of adaptation mechanisms for data-driven soft sensors [J]. Computers & Chemical Engineering, 2011, 35(1): 1-24.

[13] DAYAL B S, MACGREGOR J F. Recursive exponentially weighted PLS and its applications to adaptive control and prediction [J]. Journal of Process Control, 1997, 7(3):169-179.

[14] LIU X Q, KRUGER U, LITTLER T, et al. Moving window kernel PCA for adaptive monitoring of nonlinear processes [J]. Chemometrics and Intelligent Laboratory Systems, 2009, 96(2): 132-143.

[15] CHENG C, CHIU M S. A new data-based methodology for nonlinear process modeling [J]. Chemical Engineering Science, 2004, 59(13): 2801-2810.

[16] NAKAGAWA H, TAJIMA T, KANO M, et al. Evaluation of infrared-reflection absorption spectroscopy measurement and locally weighted partial least-squares for rapid analysis of residual drug substances in cleaning processes [J]. Analytical Chemistry, 2012, 84(4): 3820-3826.

[17] KANEKO H, FUNATSU K. Maintenance-free soft sensor models with time difference of process variables [J]. Chemometrics and Intelligent Laboratory Systems, 2011, 107(2): 312-317.

[18] KANEKO H, FUNATSU K. Classification of the degradation of soft sensor models and discussion on adaptive models [J]. AIChE Journal, 2013, 59(7): 2339-2347.

[19] GAO C H, CHEN J M, ZENG J S, et al. A chaos-based iterated multistep predictor for blast furnace ironmaking process [J]. AIChE Journal, 2009, 55(4): 947-962.

研究论文

Received date: 2015-12-21.

Foundation item: supported by the National Natural Science Foundation of China (61370029).

Adaptive soft sensor based on time difference model and locally weighted partial least squares regression

YUAN Xiaofeng, GE Zhiqiang, SONG Zhihuan
(State Key Laboratory of Industrial Control Technology, College of Control Science and Engineering, Zhejiang University, Hangzhou 310027, Zhejiang, China)

Abstract：Industrial process plants are often characterized with problems of variable drifts，nonlinearity and time-variant. The time difference (TD) model was proposed by researchers to handle the drifting problems. However, the global model used under TD model cannot describe the data characteristic like the time-variant and high nonlinearity well. Moreover, the prediction accuracy will greatly decrease when change of process state occurs. In this paper, the time difference model and locally weighted partial least squares (LWPLS) are synthesized to enhance the adaptability of soft sensor models. In the TD-LWPLS based soft sensor framework, TD is used to reduce the effect of process drifts. Moreover, as a just-in-time (JITL) method, LWPLS is utilized to tackle nonlinearity and change of process state. A numerical example and an industrial application example have been carried out to test the effectiveness and feasibility of the proposed method. The results demonstrate that the TD technique with the LWPLS model can achieve the best prediction accuracy in both cases compared to two other methods.

Key words：time difference model (TD); locally weighted partial least squares (LWPLS); just-in-time learning (JITL); soft sensor modeling; quality prediction

DOI：10.11949/j.issn.0438-1157.20151931

中图分类号：TQ 02

文献标志码：A

文章编号：0438—1157（2016）03—0724—05

Corresponding author:Prof. SONG Zhihuan, songzhihuan@zju.edu.cn