基于层次分析的FLANN神经网络研究及应用

耿志强，武开英，韩永明（北京化工大学信息科学与技术学院，北京 0009；智能过程系统工程教育部工程研究中心，北京 0009）



基于层次分析的FLANN神经网络研究及应用

耿志强1,2，武开英1,2，韩永明1,2
（1北京化工大学信息科学与技术学院，北京 100029；2智能过程系统工程教育部工程研究中心，北京 100029）

摘要：针对传统函数链接型神经网络(functional link artificial neural networks ,FLANN)不能有效处理化工过程中强耦合、带噪声的高维数据建模问题，提出了一种基于层次分析(analytic hierarchy process, AHP)的FLANN神经网络(AHP-FLANN)。通过层析分析模型过滤输入数据中的冗余信息，提取特征分量，并把提取的特征分量作为函数链接神经网络的输入进行建模。同时利用化工行业乙烯生产数据进行了验证，并和BP神经网络及FLANN神经网络进行了对比。结果表明，AHP-FLANN神经网络在处理复杂高维数据时具有收敛速度快、建模精度高、网络稳定性强等特点，同时能够指导乙烯生产，提高能效，具有良好的实用价值。

关键词：乙烯装置；生产能力预测；层次分析法；神经网络；模型预测控制；生产

2015-12-15收到初稿，2015-12-21收到修改稿。

联系人：韩永明。第一作者：耿志强（1973—），男，博士研究生，教授。

引 言

乙烯工业作为石油化工产业的龙头，其产量的高低已经成为判断一个国家工业发展水平的重要标志之一。但是在乙烯生产过程模拟与预测模型中，由于处理分组多，各种影响因素相互关联，存在极强的非线性关系。目前针对这一过程的机理虽不乏研究，但当面临生产中存在的各类复杂问题时，利用传统的数学模型很难得到解决。近年来，随着计算机技术的发展，各种人工智能方法也常被应用到生产过程模拟与预测模型中，取得了良好的效果，这些智能方法主要有专家系统[1]、遗传算法[2]、模糊理论[3]等，但是这些方法大部分是基于大样本数据的学习理论，当对少量样本数据进行预测和分析时以上方法则不一定适用。

神经网络作为一种较为先进的智能方法，近年来常被用于过程建模，同时衍生出了多种神经网络模型，如反向传播神经网络[4](BP)、多层感知机[5](MLP)等。然而，BP算法收敛速度缓慢，迭代次数常需要数千次以上。网络层数和结点数较多的情况下，计算的复杂性和计算量大大增加。其次，BP神经网络结构和MLP网络结构中隐含层结点数的选取缺少理论依据，人们往往依据经验来确定。近年来，有学者提出了函数链接型神经网络(functional link artificial neural networks，FLANN)，通过理论和实践证明FLANN[6]在预测的精度和速度上都优于MLP和BP神经网络，并且FLANN没有隐含层，这样就大大加快了网络的训练速度，计算量大为降低，有很快的收敛速度，近年来，FLANN学习算法已经在通信[7]、经济[8]、机械[9]等领域开展了研究和应用。但是该方法也存在一定的局限性：化工过程产生的数据具有强关联、高维数和非线性等特性，并且大多数化工过程都运行在比较恶劣的环境条件下，导致其测量参数不仅具有很强的耦合性，而且还经常会受到噪声干扰，严重影响FLANN的学习性能。针对高维数据建模问题，特征提取是一种有效的处理方法。常用的特征提取方法有层次分析法（AHP）、主成分分析法（principal component analysis，PCA）[10]、输入训练神经网络[11]等。其中，AHP是一种定性分析和定量分析相结合的、层次化和多准则的分析方法[12-15]，通过数据压缩、数据过滤来获得过程特征信息。本文将AHP与FLANN神经网络结合，利用AHP模型以实现冗余信息的过滤和噪声的去除，再将处理后的数据作为FLANN神经网络的输入，最终探索出了一种基于层次分析模型的AHP-FLANN神经网络。最后把该神经网络推广应用到乙烯装置生产预测中，结果验证了AHP-FLANN在处理复杂的高维数据时的有效性和可行性，为提高产品的质量、保证化工生产的安全进行提供了指导。

1 FLANN神经网络

基于函数链接的神经网络由Pao等[16]提出，其网络结构如图1所示。建立一个FLANN结构分为以下步骤。

图1 常规FLANN结构Fig.1 Conventional FLANN structure

（1）设x为n维输入向量，其中xi表示其中的第i个分量。

（2）对原始输入向量进行函数扩展，扩展后得到N维神经网络输入向量ϕ(x)。ϕ(x)=[ ϕ1(x), ϕ2(x), …, ϕk(x),…, ϕN(x)]，其中ϕk(x)为在扩展后向量的第k维向量。

（3）w为神经网络权向量，其中w=[w1,w2, …, wk,…,wN]T，将扩展函数向量ϕ(x)与全向量w相乘可得到向量的线性权重和S= ϕ(x)w。经过非线性功能函数∫(·)得到神经网络的输出结果。

常规FLANN神经网络，在对权值进行更新时一般采用BP算法，由于网络不含有隐含层，算法计算量大大减少。将网络的输出值与期望值y差值的平方和最小化min(E)作为网络的学习目标，其数学表达式为[17]

权值更新公式如下

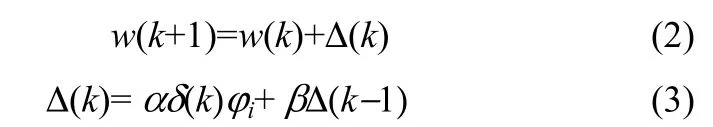
常规FLANN网络采用函数方式将原始输入模式转化到另一模式空间，再用增强后的模式代替原始模式作为输入层的输入。这种转换是非线性的而且在数学上是非线性可分的，虽没有加入新的信息，但是模式的表达却得到了增强，因而也就具有了更好的处理非线性问题的能力。另外，由于FLANN无隐含层，在数学上和应用中都证明了FLANN具有更快的学习速度且不易陷入局部极值[6]。

但是将FLANN神经网络应用于化工过程建模时，不可避免地会遇到一些问题。

（1）由于FLANN采用的是先将原始输入进行增强扩展后再输入到网络中去。而化工过程生产数据中存在着大量相互耦合的高维数据，如果直接利用还有大量冗余信息的高维数据来建模，不仅会使网络结构变得复杂，而且模型的精度也会大大降低。

（2）化工过程测量数据中常常包含一些无法避免的噪声和误差，单纯利用这些数据进行FLANN网络建模，模型鲁棒性较差，性能也会受很大影响。

2 基于层次分析法的FLANN神经网络(AHP-FLANN)

为了有效处理高维数据样本，解决传统FLANN学习算法在化工生产预测建模中存在的问题，本文结合AHP，对高维数据样本进行加权融合并提取数据特征信息。处理完成后将提取到的特征信息作为FLANN神经网络的输入。

2.1 层次分析法(AHP)

层次分析法是一种定性分析和定量分析相结合的、层次化和多准则的分析方法，利用该方法可以将乙烯生产数据燃料、电、水、蒸汽等总耗进行加权融合处理，这不仅能剔除乙烯异常数据，还能够提高乙烯数据的可比性且相对简单方便。

定义1：设装置的j参数的下侧关联函数[18]为（i指第i次采样）

其中，i=1,2, …,n; j=1,2,…,m。

设预处理后能效时序数据X=[X(1)X(2)…X(n)]T，其中，X(i)为t=i时乙烯装置的能效价值数据，且xj(2)(j=1,2,…,m) 值为平均值。得到信息阵Kn×m如下

对于n阶对称矩阵COR，根据乘积方根法（几何平均法），可以求得特征向量

具体过程如下

使用W对方案融合，得到装置能效价值融合数据Xref

由以上分析可知，利用层次分析法，可以过滤高维输入中的冗余信息，提取特征分量，有效地去除了数据中存在的噪声。

2.2 AHP-FLANN神经网络

根据2.1节提取的输入特征属性，来构建AHP-FLANN 神经网络，其组成结构图如图2所示。

图2 AHP-FLANN网络结构Fig.2 AHP-FLANN network structure

给定K个具有高维输入的不同训练样本集合S={(Xk,Yk)|k=1,2,…,K; Xk∈RI;Yk∈RJ}，其中每个训练样本的输入含有I个属性，输出含有J个属性。对于训练样本S，采用基于层次分析法的AHP-FLANN神经网络建模如下。

（1）层次分析模型建立。将训练样本集合S中的高维输入向量作为层次分析模型的输入向量。利用该模型得到数据的特征分量，进而得到经过特征提取的新的样本集合S′={(Xm,Yk)|m=1,2,…,M; k=1,2,…,K; Xm∈RL;Yk∈RJ}。其中RL为经过特征提取后得到的新的样本输入集合，包含L个样本属性。

（2）FLANN神经网络建立。将步骤（1）得到的样本集合S′作为FLANN神经网络的输入，而训练样本集合S中的向量{Yk|k=1,2,…,K; Yk∈RJ}作为FLANN神经网络的期望输出。由于数据中各个变量的量纲一般并不相同，使得变量之间的数值没有可比性，因此在训练之前需要对数据集进行归一化处理。采用下面转换公式

（3）训练过程。首先，将步骤（2）得到的经过归一化后的神经网络输入进行函数扩展，扩展后得到N维神经网络输入向量ϕ(x)=[ ϕ1(x), ϕ2(x),…, ϕk(x),…, ϕN(x)]。其中ϕk(x)为在扩展后向量的第k维向量。然后，利用FLANN神经网络采用梯度下降算法进行训练，记录训练后的FLANN神经网络输入层与输出层之间的权值连接矩阵W。

（4）回想过程。根据步骤（3）训练所得的AHP-FLANN神经网络，再次利用训练样本集合S′={(Xm,Yk)|m=1,2,…,M; k=1,2,…,K; Xm∈RL; Yk∈RJ}计算AHP-FLANN神经网络的回想输出{Dk|k=1,2,…,K; Dk∈RL}，利用式（11）对输出进行反归一化

（5）泛化过程。采用一组不同于训练样本的数据集合，作为AHP-FLANN神经网络的泛化样本集合S″={(X′m, Y′k)|m=1,2,…, M′; k=1,2,…,K′; X′m∈RL; Y′k∈RJ}。同理，利用集合S″计算训练好的AHP-FLANN神经网络泛化输出{D′k|k=1,2,…, K′; D′k∈RL}，将其与期望输出{Y′k|k=1,2,…,K′; Y′k∈RJ}进行比较，计算网络的泛化相对误差和泛化标准差。

3 实验测试

3.1 乙烯投入产出数据分析

在乙烯工业中，不同的乙烯能效分析界区和计算方法被不同企业所采用。因此，为更好地分析乙烯装置能效，本文参照乙烯行业标准DB 37/751—2007和GB/T 2589—2008进行乙烯生产装置界区的划分。

对于乙烯装置而言，与生产效率直接相关的因素主要包括：①原料；②燃料、动力消耗；③产品。由乙烯生产能量界区可知：原油、燃料、蒸汽、水、电作为乙烯生产的投入指标，而主要生产的乙烯、丙烯、碳四[19-22]的产量为产出指标。同时表示乙烯装置能耗水平比较通用的方法是按照《石油化工设计能量消耗计算方法》（SH/T 3110—2001）中的表3.0.2和表3.0.3的换算关系将能耗相关参数中的燃料、蒸汽、水、电的计量单位统一换算成GJ，原油、乙烯、丙烯、碳四生产单位以t计量。故本文将燃料、蒸汽、水、电，再加上原油作为神经网络的输入，乙烯、丙烯及碳四产量之和作为神经网络的输出。

3.2 乙烯装置生产预测分析

为了验证本文提出的基于层次分析的函数链接神经网络的可行性和有效性，本文选取全国7种主要乙烯生产技术中19个乙烯生产装置2009～2013年的月生产数据为分析对象。首先，选取某生产装置2010年原油(石脑油、轻柴油、抽余油、加氢尾油1、加氢尾油2、碳三四五、其他)、燃料（轻质油、重质油、燃料气）、蒸汽（超高压蒸汽、高压蒸汽、中压蒸汽、低压蒸汽）、水（循环水、工业水、锅炉积水、其他水）、电这5大类原料作为网络的输入，将产物乙烯、丙烯、碳四产量之和作为网络的输出，由上所述最终构成19输入单输出训练样本数据。接着，利用层次分析模型对4大类输入原料进行特征提取，提取之后神经网络输入由原来的19个变成了5个。最后，将经过特征提取的数据输入FLANN神经网络进行预测建模。

图3 训练误差变化趋势Fig.3 Variation trend of training error

设单层BP网络的学习因子为0.1，动量因子为0.9，迭代次数为1000次，激励函数为S型函数。输入层、隐含层、输出层的节点数分别为19，25，1。FLANN网络学习因子为0.1，迭代次数为100次，输入层和输出层节点数为19和1。AHP-FLANN网络学习因子为0.1，迭代次数为100次，输入层和输出层节点数为5和1。选用2010年的200组真实乙烯生产装置数据建立模型，并对2011年乙烯装置产出进行模拟，结果如图3、图4所示。图3为网络训练过程中相对误差变化趋势，图4记录了利用训练好的网络对2011年乙烯装置生产产量进行预测。

图4 AHP-FLANN泛化曲线Fig.4 Generalization curve of AHP-FLANN

由图3可以看出当网络迭代次数达到8次时，网络训练相对误差几乎不再变化，网络收敛速度极快。对于处理工业中产生的大量复杂数据，无疑有巨大的优势。由图4可以看出由AHP-FLANN神经网络预测的2011年乙烯装置产出值非常接近2011年乙烯装置的实际产出，经过计算，AHP-FLANN网络训练的平均相对误差为0.0512，而网络泛化的平均相对误差为0.0549。

为了更进一步验证AHP-FLANN神经网络的可行性，本文又建立了BP神经网络模型和传统FLANN神经网络模型来进行对比验证。选用2009年的216组真实生产数据分别对以上两种网络进行建模，并对2011年乙烯装置产出进行模拟，并和本文提出的神经网络进行对比。各个模型的预测精度、运行时间对比如表1和图5所示。

表1 BP、FLANN、AHP-FLANN训练、泛化平均相对误差及运行时间对比Table 1 Relative error of network training, generalization and comparison of running time

由表1可以看出AHP-FLANN的训练结果较BP和FLANN更接近真实值，AHP-FLANN神经网络泛化相对误差为5.51%；而BP神经网络和FLANN神经网络的训练相对误差分别为7.16%和10.66%。其次，AHP-FLANN网络对乙烯产量预测结果的标准差相对于其他两种网络更小。因此利用AHP-FLANN神经网络进行预测，可以更快、更小误差、更稳定地预测某一年的乙烯生产量。而就整个网络训练泛化过程所需要的时间而言，AHP-FLANN明显更快，它比BP网络约快6倍，而比传统FLANN网络约快3倍。

图5 BP、FLANN、AHP-FLANN泛化结果比较Fig.5 Comparison of generalization results

3.3 乙烯装置生产能效分析

本文选取相同规模（80万吨级）不同技术下的两套乙烯生产装置。首先对两套乙烯装置2010年的能耗数据基于式(4)～式(9)进行层次融合，然后基于FLANN建立预测模型，预测2011年乙烯、丙烯和碳四的总产量。两套装置产量的预测结果方法平均误差分别如图6和表2所示。

图6 不同乙烯生产装置结果预测Fig. 6 Prediction of different ethylene production plant

表2 不同乙烯生产装置泛化平均误差对比Table 2 Comparison of average error of different ethylene production units

由图6和表2可以看出，用AHP-FLANN网络预测乙烯生产装置产量在两条生产线上都比用FLANN进行预测更加准确。进一步说明了AHPFLANN网络具有更高的预测精度。第一套乙烯生产装置的泛化相对平均误差均小于第二套乙烯生产装置，说明该生产装置下乙烯的产量稳定，生产状况良好，而第二套乙烯生产装置的乙烯产量波动较大，说明该生产装置出现生产能效低下的状况，可以根据生产状况调整乙烯投入量或者引入第一种技术，能够改进乙烯生产状况，达到生产稳定，提高乙烯能效。例如第一套装置2011年7月投入原油296892 t，燃料19.19 GJ，蒸汽0.48 GJ，水2.93 GJ，电0.74 GJ，而实际乙烯、丙烯、碳四的产出总量为168425 t，预测模型产出量为165377.13 t，输出结果在误差范围内，说明7月份中该装置满负荷运行，在后续生产中该装置可维持该生产状况。第二套生产装置2011年6月投入原油58851 t，燃料18.78 GJ，蒸汽2.81 GJ，水1.75 GJ，电1.93 GJ，乙烯、丙烯、碳四的产出总量为17987 t，预测模型产出为33535 t，说明6月份该装置能效低下，在以后生产中应该调整投入产出，提高生产效率。

4 结 论

针对化工过程数据高维数、强关联、非线性等特点，为了解决传统神经网络在处理化工过程数据时收敛速度慢、输入节点多的问题，本文提出了一种AHP-FLANN模型，该网络模型运用层次分析法过滤掉数据中的冗余信息，提取出数据的特征变量，并采用FLANN神经网络进行训练，优化了神经网络处理化工数据的能力。通过对乙烯装置生产建模的应用，结果表明，AHP-FLANN神经网络相比于单独的FLANN神经网络，以及传统的BP神经网络，不仅具有信息压缩、数据提取、噪声抑制的能力，而且网络结构简单、训练速度快、泛化性能好。将所提出的AHP-FLANN神经网络应用于复杂化工过程建模，能够较准确地预测乙烯生产效率情况，指导乙烯生产，提高能效，同时提出的算法还可以应用到其他化工工业预测建模中。

References

[1] 张绍兵, 季厌浮, 高志军. 基于神经网络专家系统的研究与实现[J]. 计算机工程与科学, 2008, (4): 156-158.

ZHANG S B, JI Y F, GAO Z J. Research and implementation of an expert system based on neural networks [J]. Computer Engineering and Science, 2008, (4): 156-158.

[2] 杨国军, 崔平远, 李琳琳. 遗传算法在神经网络控制中的应用与实现 [J]. 系统仿真学报, 2001, (5): 567-570.

YANG G J, CUI P Y, LI L L. Applying and realizing of geneticalgorithm in neural networks control [J]. Journal of System Simulation, 2001, (5): 567-570.

[3] 严宇, 刘天琪. 基于神经网络和模糊理论的电力系统动态安全评估 [J]. 四川大学学报(工程科学版), 2004, (1): 106-110.

YAN Y, LIU T Q. Dynamic security assessment of power system based on ann and fuzzy theory [J]. Journal of Sichuan University (Engineering Science Edition), 2004, (1): 106-110.

[4] DING S F, SU C Y, YU J Z. An optimizing BP neural network algorithm based on genetic algorithm [J]. Artificial Intelligence Review, 2011, 36(2): 153-162.

[5] MOALLEM P, MONADJEMI S A. An efficient MLP-learning algorithm using parallel tangent gradient and improved adaptive learning rates [J]. Connection Science, 2010, 22(4): 373 - 392.

[6] 徐科军, 殷铭.基于FLANN的腕力传感器动态建模方法 [J]. 仪器仪表学报, 2000, 21(1): 92-94.

XU K J, YIN M. A dynamic modeling method based on FLANN for wrist force sensor [J]. Chinese Journal of Scientific Instrument, 2000, 21(1): 92-94.

[7] MISHRA S K, PANDA G, MEHER S, et al. Exponential functional link artificial neural networks for denoising of image corrupted by Gaussian noise[C]// Proceedings of the 2009 International Conference on Advanced Computer Control. Washington, DC, USA: IEEE Computer Society, 2009: 355-359.

[8] MAJHI R, PANDA G, SAHOO G. Development and performance evaluation of FLANN based model for forecasting of stock markets [J]. Expert Systems with Applications: An International Journal, 2009, 36(3): 6800-6808.

[9] HUANG S L, HAO K S, ZHAO W. New improved FLANN approach for dynamic modelling of sensors [J]. International Journal of Computer Applications in Technology, 2011, 41(1/2): 4-10.

[10] LEE J M, YOO C K, CHOI S W, et al. Nonlinear process monitoring using kernal principal component analysis [J]. Chem. Eng. Sci., 2004, 59(1): 223-234.

[11] GENG Z Q, ZHU Q X. Multiscale nonlinear principal component analysis(NLPCA) and its application for chemical process monitoring [J]. Ind. Eng. Chem. Res., 2005, 44(10): 3585-3593.

[12] PASCOE S, BUSTAMANTE R, WILCOX C, et al. Spatial fisheries management: a framework for multi-objective qualitative assessment [J]. Ocean & Coastal Management, 2009, 52(2): 130-138.

[13] 孙才志, 林学钰. 基于层次分析的模糊一致性判断矩阵及其应用[J]. 模糊系统与数学, 2002, 16(3): 59-63.

SUN C Z, LIN X Y. Fuzzy consistent matrix based on AHP and its application [J]. Fuzzy Systems and Mathematics, 2002, 16(3): 59-63.

[14] 魏翠萍. 层次分析法中和积法的最优化理论基础及性质 [J].系统工程理论与实践, 1999, 9: 113-115

WEI C P. The optimization basis and properties of the sum-product method in AHP [J]. Systems Engineering - Theory & Practice, 1999, 9: 113-115.

[15] 演克武,朱金福,何涛.层次分析法在多目标决策过程中的不足与改进 [J]. 统计与决策, 2007, 5: 10-11.

YAN K W, ZHU J F, HE T. Inadequate and improved multi-objective decision-making process in AHP [J]. Statistics and Decision, 2007, 5: 10-11.

[16] PAO Y H, PHILIPS S M, SOBAJIC D J. Neural-net computing and intelligent control systems [J]. International Journal of Control, 1992, 56(2): 263-289.

[17] 叶世伟, 史忠植. 神经网络原理[M].北京: 机械工业出版社, 2004: 10-12.

YE S W, SHI Z Z. Neural Networks:A Comprehensive Foundation [M]. Beijing: China Machine Press, 2004: 10-12.

[18] HAN Y M, GENG Z Q, LIU Q Y. Energy efficiency evaluation based on data envelopment analysis integrated analytic hierarchy process in ethylene production [J]. Chinese Journal of Chemical Engineering , 2014, 22(12): 1279-1284.

[19] 耿志强, 朱群雄, 顾祥柏.基于关联层次模型的乙烯装置能效虚拟对标及应用 [J].化工学报, 2011, 62(8): 2372-2377.

GENG Z Q, ZHU Q X, GU X B. Dependent function analytic hierarchy process model for energy efficiency virtual benchmark and its applications in ethylene equipments [J]. CIESC Journal, 2011, 62(8): 2372-2377.

[20] GENG Z Q, HAN Y M, YU C P. Energy efficiency evaluation of ethylene product system based on density clustering data envelopment analysis model [J]. Advanced Science Letters, 2012, 5: 1-7.

[21] 王学雷. 面向乙烯生产流程的能源消耗动态定标方法 [J].计算机与应用化学, 2010, 27(9): 1166-1170.

WANG X L. A dynamic benchmarking method for energy consumption of ethylene production process [J]. Computers and Applied Chermistry, 2010, 27(9): 1166-1170.

[22] GENG Z Q, HAN Y M, GU X B, et al. Energy efficiency estimation based on data fusion strategy: case study of ethylene product industry [J]. Industrial & Engineering Chemistry Research, 2012, 51: 8526-8534.

研究论文

Received date: 2015-12-15.

Foundation item: supported by the National Natural Science Foundation of China (61374166, 61533003), the Specialized Research Fund for the Doctoral Program of Higher Education of China (20120010110010), and the Fundamental Research Funds for the Central Universities (YS1404, JD1502).

Research and application of FLANN neural network based on AHP

GENG Zhiqiang1,2, WU Kaiying1,2, HAN Yongming1,2
(1College of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, China;2Engineering Research Center of Intelligent PSE, Ministry of Education in China, Beijing 100029, China)

Abstract:The traditional functional link artificial neural network (FLANN) is inefficient in the high-dimensional data modeling of the chemical process, where the data has characteristics of multi-dimensional, strongly coupled and noisy. In order to dealing with this problem, the FLANN based on analytical hierarchy process (AHP-FLANN) is proposed. The analytical hierarchy process (AHP) is constructed to filter redundant information and extract characteristic components. And then these characteristic components are trained by the FLANN. Meanwhile, the proposed AHP-FLANN method is applied to analyze the ethylene production data in the chemical industry. Compared with the BP network and the FLANN, the AHP-FLANN has the advantages of fast convergence speed with high modeling accuracy and strong network stability. The experimental result shows that the proposed method can guide the ethylene production conditions and improve the efficiency of energy utilization during ethylene production process. It has the practical value in practice.

Key words：ethylene plant；production capacity forecast；analytic hierarchy process；neural networks；model-predictive control；production

DOI：10.11949/j.issn.0438-1157.20151911

中图分类号：TP 29

文献标志码：A

文章编号：0438—1157（2016）03—0805—07

基金项目：国家自然科学基金项目（61374166, 61533003）；高等学校博士学科点专项科研基金（20120010110010）；中央高校基本科研业务费（YS1404，JD1502）。

Corresponding author:HAN Yongming, hanym @mail.buct.edu.cn