强震记录下钢结构建筑非线性阻尼比研究

马　俊

(同济大学 土木工程学院，上海 200092)



强震记录下钢结构建筑非线性阻尼比研究

马俊

(同济大学 土木工程学院，上海 200092)

摘要：为了研究钢结构建筑阻尼特性，采用希尔伯特-黄变换和随机减量技术，从强震记录中识别钢结构建筑基于振动幅度的非线性阻尼比。结果表明，钢结构建筑的阻尼比具有明显的基于振幅的非线性特性。在初始阶段，阻尼比随振幅的增大而上升，当振幅越过“临界振幅”后，阻尼比随振幅增长呈现下降趋势。基于希尔波特-黄变换和随机减量技术，可以从强震记录中对基于振幅的非线性阻尼比等模态参数进行识别。

关键词：钢结构；非线性阻尼比；振动幅度；希尔伯特-黄变换；随机减量技术

阻尼是描述结构在振动过程中摩擦耗能的重要参数，机理较为复杂，目前尚没有明确的理论和计算方法。虽然在工程应用中，通常采用常阻尼模型，但是近年来的国内外研究表明，钢结构建筑的阻尼比具有明显的基于振动幅度的非线性特性[1-7]。钢结构建筑的阻尼比随激励幅度的增大而提高，甚至当激励幅度越过“临界振幅”时，阻尼比表现出随激励幅度的增大而降低的特性[8]。文献[5]研究表明采用常阻尼模型进行动力分析可能会低估结构的动力响应。可见，目前采用的常阻尼模型与钢结构建筑的实际阻尼特性间存在着差异，可能会低估结构响应，因此需要对钢结构建筑的基于振动幅度的非线性阻尼特性进行深入研究。目前国内外关于钢结构建筑基于振幅的非线性阻尼特性研究较少，已有的研究大多集中在微小振动范围。本文对一钢结构高层建筑在东日本大地震中的实测地震响应数据进行分析，采用希尔伯特-黄变换和随机减量技术，在地震波激励下识别钢结构建筑基于振幅的非线性阻尼比，研究钢结构建筑在高振幅范围下的非线性阻尼特性。

1 钢结构建筑概况

日本东京都墨田区市政厅为钢结构建筑，地上结构20层(含塔楼)，地下2层，建于1990年，建筑总高度84.71 m。在该建筑的B1层、8层和20层(塔楼)各布置有1个加速度传感器，用以观测建筑的地震反应。每个加速度传感器可以同步记录纵横两个水平方向和竖直方向的结构加速度响应数据，加速度传感器的采样频率为100 Hz。该钢结构建筑在2011年3月11日东日本大地震(M=9.0)中记录到了丰富的结构地震反应记录[9]，B1层记录到的加速度响应峰值在横向(X向)为0.69 m/s2，在纵向(Y向)为0.66 m/s2，相应方向上的20层加速度响应峰值分别为-3.85 m/s2和-2.90 m/s2，B1层和20层的加速度响应数据如图1所示。

2 模态参数识别方法

钢结构建筑在地震波激励下的结构动力响应是典型的非线性非平稳响应，常用的频域和时域模态参数识别算法并不能有效的从地震反应记录中识别模态参数。本文采用希尔伯特-黄变换(Hilbert-Huang Transform，HHT)和随机减量技术(Random Decrement Technique，RDT)，从地震响应信号中识别钢结构建筑基于振幅的非线性阻尼比。希尔伯特-黄变换是一类处理非线性非平稳信号的时频分析方法，可以对非线性非平稳信号进行平稳化处理。随机减量技术是从平稳随机响应信号中提取确定性响应的信号分析算法，可以从平稳随机信号中提取自由衰减函数。

2.1 希尔伯特-黄变换

希尔伯特-黄变换是Huang等[10]提出的一种针对非线性非平稳信号的数据处理方法，由经验模态分解(Empirical Mode Decomposition，EMD)和希尔伯特变换(Hilbert Transform，HT)两部分组成，其核心是经验模态分解。经验模态分解认为任何信号都可以被分解为一组包含不同时间尺度的本征模态函数(Intrinsic Mode Function，IMF)，每个本征模态函数都需满足以下两个条件：(1)整个时间序列上的极值点数目与过零点数目相同或至多相差一个；(2)在任意点由极大值构成的上包络线与极小值构成的下包络线的平均值为零。基于上述条件，经验模态分解对非平稳数据进行了平稳化处理，得到一组近似平稳的本征模态函数。

经验模态分解的步骤可以简要描述如下。针对原始数据信号x(t)，首先找出所有的极值点，用三次样条曲线连接所有极大值点形成上包络线，对所有极小值做相同处理形成下包络线，对上、下包络线取平均，得到瞬时平均值m1(t)，用原始数据x(t)减去瞬时平均值m1(t)，得到消除低频的新信号h(t)。若h(t)满足本征模态函数的两个条件，则h(t)即为第一个本征模态函数c1(t)，若不满足，则h(t)将做为原始信号，重复上述筛选过程，直到经过k次筛选后的信号hk(t)满足本征模态函数的条件，将hk(t)做为第一个本征模态函数c1(t)。随后，从原始信号x(t)中减去第一个本征模态函数，得到频率较低的残余量r1(t)，将r1(t)做为新的信号重复上述筛选过程，直到经过n次筛选后的余量rn(t)成为单调函数或小于预先设定的阈值，此时原始数据信号被分解为n个本征模态函数和1个余量rn(t)，记为，

(1)

通过上述分解步骤，原始信号按照时间尺度从小到大的顺序被分解为一组本征模态函数，其中第一阶本征模态函数包含了时间尺度最小、频率成分最高的信号成分，残余量则包含了频率成分最低的信号成分。

2.2 随机减量技术

随机减量技术是Cole[11]提出的一种针对平稳随机信号的模态识别技术，其基本思想认为平稳随机响应信号包括由初始条件决定的确定性响应和由外部荷载决定的随机响应两部分组成，利用随机响应部分的平均值接近零的特点，可以采用样本平均技术从平稳随机响应中提取出确定性响应部分，即与外部荷载无关的自由响应信号。

随机减量技术的步骤简要描述如下。针对平稳随机的原始数据信号y(t)，通过设置截取常数和截取时间长度τ，可以将原始数据信号分解为2N个子信号函数y(ti+τ,c)，每个子函数信号的初始时间点为ti，初始振幅为c，时间长度为τ。采用样本平均技术对y(ti+τ,c)进行统计平均，从而得到初始振幅为c、时间长度为τ的随机减量信号，即与外部荷载无关的自由衰减函数，记为，

(2)

2.3 基于振幅的非线性阻尼比识别方法

采用希尔伯特-黄变换和随机减量技术，可以从地震波激励下识别钢结构建筑的基于振动幅度的非线性阻尼比。首先，对原始信号进行滤波处理，提取目标模态的模态响应。根据原始数据信号的傅立叶谱，可以得到目标模态的大致分布范围。采用带通滤波等技术，实现目标模态信息提取；其次，采用经验模态分解将目标模态响应信号分解为本征模态函数，其中第一阶本征模态函数包含了目标模态的最高频成分，可以近似为对应的目标模态响应；再者，利用随机减量技术从第一阶本征模态函数中提取自由振动信号。通过改变截取常数，可以得到一组截取常数值及一组与之对应的自由衰减函数；最后，采用曲线拟合技术对自由衰减函数进行拟合，识别基于振幅的阻尼比等模态参数。通过对截取常数对应的自由衰减函数进行拟合，可以得到截取常数对应的阻尼比等模态参数。截取常数同时也是自由衰减函数的初始振幅，从而得到了基于振幅的非线性阻尼比等模态参数。曲线拟合公式记为，

(3)

式中：a(t)为自由衰减函数；a0为初始振幅；ωn为无阻尼固有频率；ζ为阻尼比。

3 模态识别过程与结果

本文选取墨田区市政厅的20F测点在东日本大地震中的加速度响应数据进行分析，使用希尔伯特-黄变换和随机减量技术识别该建筑基于振动幅度的阻尼比等模态参数。加速度响应记录的傅立叶功率谱如图2所示。图2(a)显示结构在X方向的前3阶频率分别约为0.5、1.5、2.5Hz，其中X向第1阶频率范围大致在0～1Hz。图2(b)显示结构在Y方向的前3阶频率分别约为0.6、1.7、3.1Hz，其中Y向第1阶频率大致在0～1Hz之间。

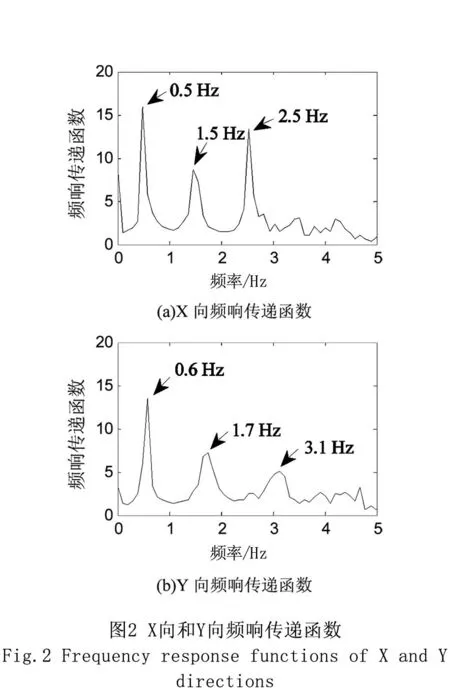
针对X向和Y向第1阶模态，采用带通滤波技术进行滤波处理后，分别对所得到的模态响应信号进行经验模态分解，计算相应的本征模态函数。图3显示了X向第1阶模态的模态响应信号、对应的前3阶本征模态函数及残余量，本征模态函数在时间尺度上表现为从小到大的分解，第一阶本征模态函数包含了模态响应信号的最高频成分，在时域上最接近模态响应信号，残余项则接近单调函数。

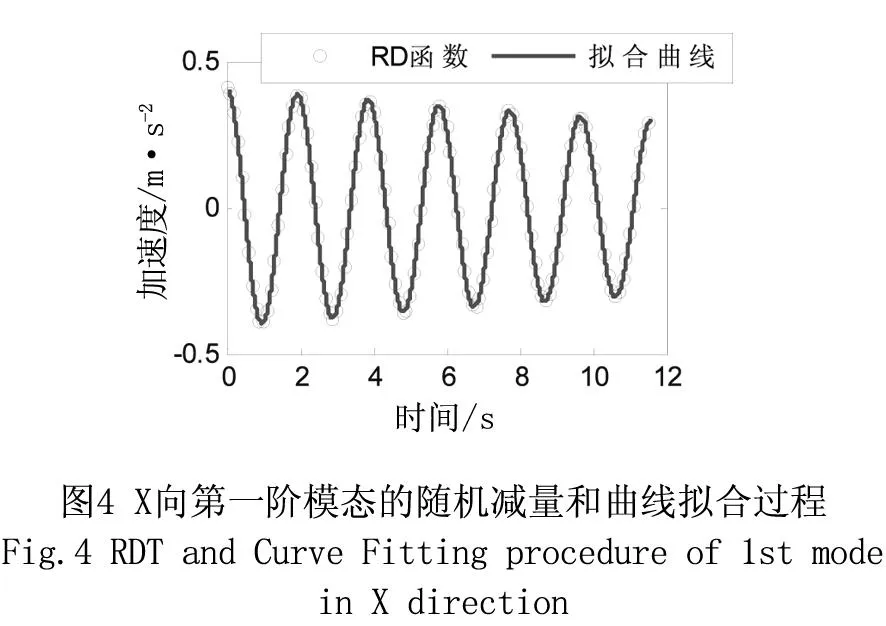
采用随机减量技术对X向和Y向第一阶本征模态函数进行处理，得到相应的自由衰减函数。随机减量过程中，截取常数在0～0.6m/s2之间，截取时间长度为12s。通过对自由衰减函数进行曲线拟合，即可得到对应截取常数的阻尼比。图4显示了X向第1阶模态的随机减量及曲线拟合过程，自由衰减趋势比较明显，曲线拟合结果也很好，误差仅为0.4%。

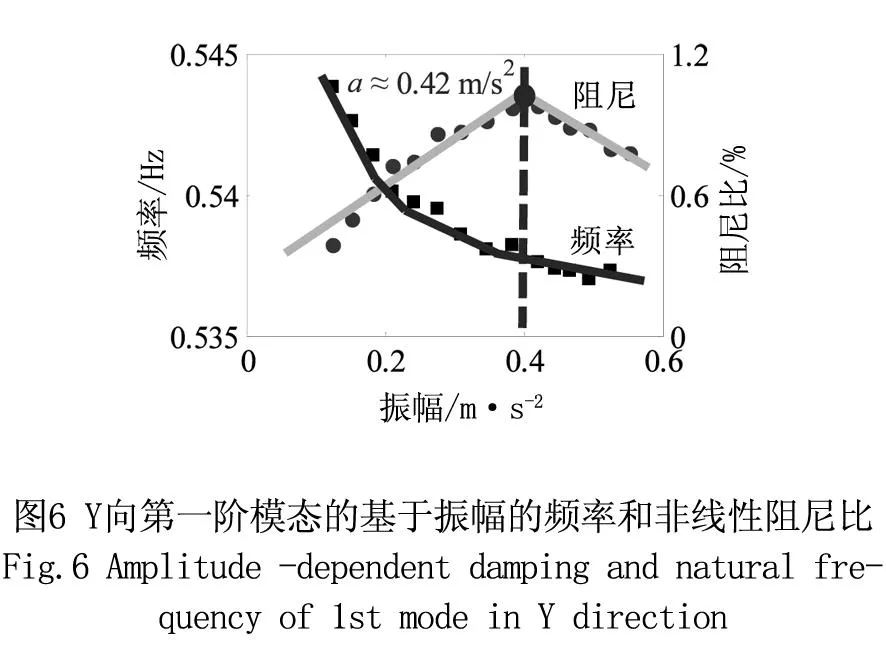
结构X向和Y向第1阶模态的识别结果分别如图5和图6所示。图5显示了X向第1阶模态的基于振动幅度的非线性阻尼比和固有频率。从图中可见，阻尼表现出明显的基于振幅的非线性特性。当振幅在0～0.41 m/s2范围时，随着振幅的增大，阻尼比持续上升。当振幅越过0.41 m/s2时，随着振幅的增大，阻尼比呈下降趋势。固有频率随振幅的增大持续下降，但其下降速率在不同振幅范围下有所区别。在0～0.1 m/s2范围时，固有频率随振幅下降较快，随后呈现缓慢下降趋势。图6显示了Y向第1阶模态的基于振动幅度的非线性阻尼比和固有频率，阻尼比和频率表现出与X向相似的变化规律。当振幅在0～0.42 m/s2范围时，阻尼比随振幅呈上升趋势，随后阻尼比随着振幅的增大而下降。固有频率则随振幅增大呈现下降趋势。

4 结论

本文使用希尔伯特-黄变换和随机减量技术，从强震记录中识别了一栋钢结构建筑的非线性阻尼比，研究了钢结构建筑基于振动幅度的非线性阻尼特性。结果表明，钢结构建筑的阻尼比具有明显的基于振动幅度的非线性特性，阻尼比在初始阶段随振幅的增大而上升，当振幅越过“临界振幅”时，阻尼比随振幅增长呈现下降趋势。采用希尔伯特-黄变换和随机减量技术，可以从地震记录中对基于振幅的非线性阻尼比等模态参数进行识别。

参考文献：

[1]GB50011-2010,建筑抗震设计规范[S].

[2]FUKUWA N,NISHIZAKA R,YAGI S,et al.Field measurement of damping and natural frequency of an actual steel-framed building over a wide range of amplitudes[J].Journal of Wind Engineering and Industrial Aerodynamics,1996, 59(2-3): 325-347.

[3]JEARY A P.Damping in tall buildings-a mechanism and a predictor[J].Earthquake Engineering and Structural Dynamics,1986,14(5): 733-750.

[4]LAGOMARSINO S.Forecast models for damping and vibration periods of buildings[J].Journal

of Wind Engineering and Industrial Aerodynamics,1993, 48(2-3): 221-239.

[5]LI Q S,YANG K,WONG C K,et al.The effect of amplitude-dependent damping on wind-induced vibrations of a super tall building[J].Journal of Wind Engineering and Industrial Aerodynamics,2003,91: 1175-1198.

[6]LI Q S,XIAO Y Q,WONG C K,et al.Field measurements of typhoon effects on a super tall building[J]. Engineering Structure,2004,26: 233-244.

[7]TAMURA Y,SUGANUMA S.Evaluation of amplitude-dependent damping and natural frequency of building during strong wind[J].Journal of Wind Engineering and Industrial Aerodynamics,1996,59:115-130.

[8]OKADA K,NAKAMURA Y,SHIBA K,et al.Forced vibration tests of ORC200 symbol tower,part 1 test methods and results[J].Summaries of Technical Papers of the Annual Meeting of Architectural Institute of Japan.1993, Structures 1:875-876. (in Japanese)

[9]TOSHIHIDE K,KOYAMA S,OKAWA I.Strong Motion Records in Buildings from the 2011 off the Pacific coast of Tohoku Earthquake,Building Research Data No.135[R]. Building Research Institute,2012. (in Japanese)

[10]HUANG N E,SHEN Z,LONG S R,WU M C,SHIH H H,ZHENG Q,YEN N C,TUNG C C,Liu H H.The Empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proceedings of the Royal Society A,1998,454:903-995.

[11]COLE H A.On-line failure detection and damping measurement of aerospace structure by random decrement signature[M].Washington:National Aeronautics and Space Administration,1973.

(责任编辑李军)

Evaluation of amplitude-dependent damping of steel buildings from strong motion records

MA Jun

( Department of Building Engineering, Tongji University, Shanghai, 200092, China)

Abstract：This paper adopts Hilbert-Huang Transform and Random Decrement Technique to evaluate amplitude-dependent damping of a steel building from strong motion records. The results demonstrate that amplitude-dependent damping is an inherent nature of steel buildings. Damping first increases with amplitude at the initial stage, then starts decreasing with amplitude after reaching a "critical amplitude". Based on Hilbert-Huang Transform and Random Decrement Technique, it is feasible to identify nonlinear damping ratios with respect to amplitude from strong motion records.

Key words：steel building; nonlinear damping ratio; amplitude; Hilbert-Huang Transform; Random Decrement Technique

中图分类号：TU393.2

文献标识码：A

文章编号：1673-9469(2016)01-0001-04

doi:10.3969/j.issn.1673-9469.2016.01.001

作者简介：马俊(1986-)，男，浙江德清人，博士，从事钢结构方面研究。

基金项目：国家建设高水平大学公派研究生项目(101206260029)

收稿日期：2015-10-30