公路桥梁限载标准安全性分析
潘腾飞,李松辉,王彦伟
(山东科技大学 土木工程防灾减灾重点实验室,山东 青岛 266590)
公路桥梁限载标准安全性分析
潘腾飞,李松辉,王彦伟
(山东科技大学 土木工程防灾减灾重点实验室,山东 青岛 266590)
摘要:以山东省某预应力混凝土空心板桥为依托,系统验证已有桥梁限载分析模型的工程安全性。首先,根据该桥结构设计资料,按《公路钢筋混凝土及预应力混凝土桥涵设计规范》设计汽车荷载进行承载能力检算,验证桥梁是否达到设计要求;在此基础上,针对不同的限载安全等级,按设计采用的车辆横向布载模式,计算典型限载车辆荷载作用下的荷载效应与跨中挠度;与设计汽车荷载产生的荷载效应和跨中挠度进行对比,检验所提限载取值对该类桥梁的工程安全性。计算结果表明,与安全等级一级和二级对应的典型限载车辆,可以满足安全等级一级、二级和三级的承载能力要求;与安全等级三级对应的典型限载车辆,可以满足安全等级一级、二级和三级的正截面承载能力要求,但不能满足安全等级一级的斜截面抗剪承载力要求。
关键词:预应力空心板桥;桥梁限载;典型限载车辆;极限状态;安全性分析
目前,随着我国交通运输业的快速发展,超重运输已成为制约我国公路事业可持续发展的主要因素之一,其不但严重影响桥梁结构的耐久性能,增加桥梁养护维修费用,更是导致桥梁损伤甚至垮塌的首要因素,因此,系统开展桥梁限载理论方面的研究已刻不容缓。针对桥梁限载取值问题,国外学者做了一定研究,美国国家公路工作者协会(AASHO)基于设计汽车荷载即为桥梁限载值的假定,针对HS-20与H-15荷载等级桥梁建立了统一的桥梁限载公式(Federal Bridge Formula或Bridge Formula B)[1];Ghosn等[2-3]首次应用结构可靠度理论对现行桥梁限载公式进行了可靠性校准,进而按现有抗力与荷载效应分布函数推算相应的目标可靠指标,并确保该安全水平下小跨径桥梁满足相应的使用性能要求,建立了新的限载公式。本文针对李松辉[4]提出的桥梁限载标准,以预应力空心板桥为例,采用典型限载车辆加载方式,系统的检算了桥梁承载能力极限状态和正常使用极限状态各项指标, 经与现行限载标准对比,以检验该桥梁限载标准的工程适用性。提出的典型限载车辆是兼顾新旧设计规范因素的桥梁限载取值分析模型,且简洁明了的实现了限载取值的统一,有利于公路路政部门查超、治超以及超限审批工作的开展,具有重要的学术和实用价值。
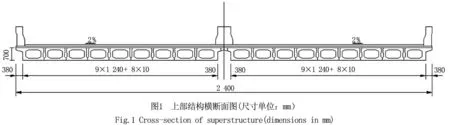
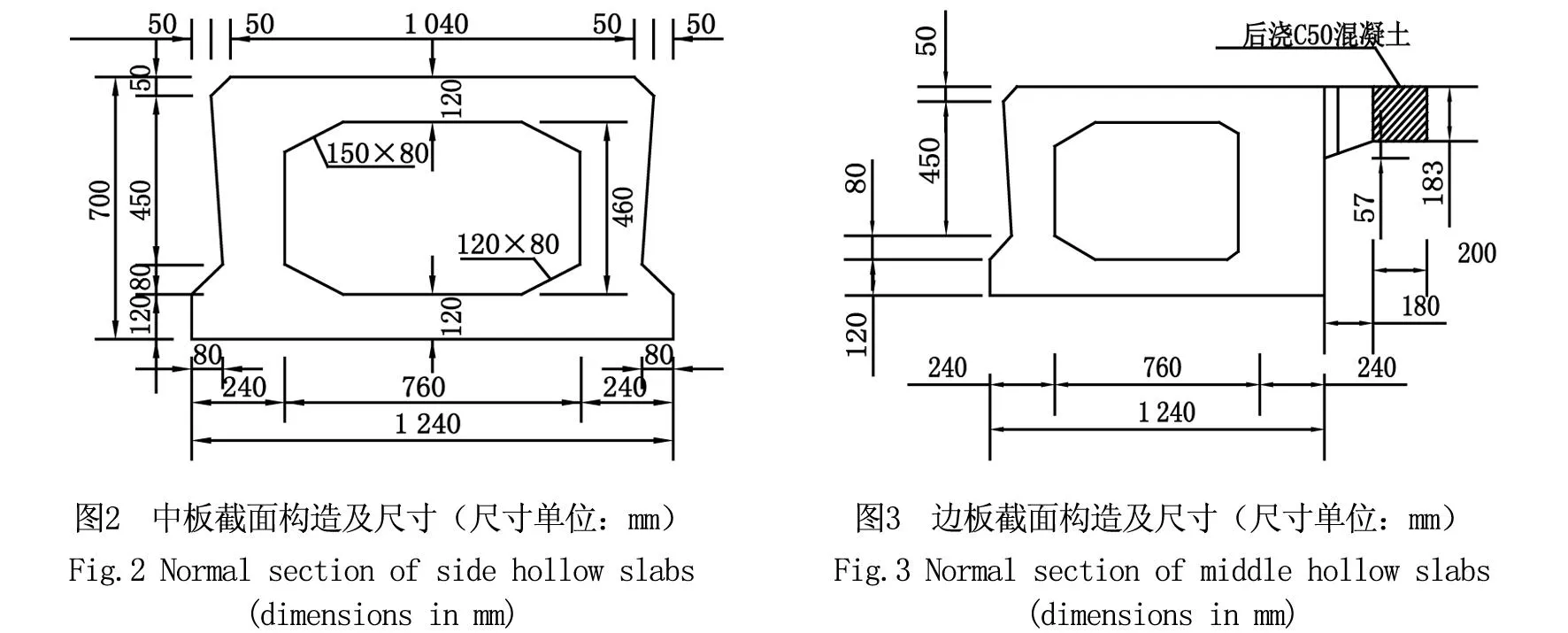
1 桥梁概况
玉平沂河大桥位于临沂市区北部,为预应力混凝土空心板桥,标准跨径13 m,计算跨径12.6 m,设计荷载等级为公路-Ⅰ级。桥面净空23 m,全桥采用18块C50的预制预应力混凝土空心板,每块空心板宽1 240 mm,高70 mm,空心板全长12.96 m。采用后张法施工工艺,预应力钢筋采用17股钢绞线,直径15.2 mm,非预应力钢筋采用HRB335、HPB235,预制空心板、封锚端、铰缝和桥面现浇层均采用C50混凝土;桥面铺装采用100 mm厚C50沥青混凝土。上部结构横断面布置如图1所示。
2 按设计汽车荷载进行承载能力检算
2.1 桥梁跨中截面抗弯承载能力验算
边板、中板横断面如图2、图3所示,按《公路桥涵设计通用规范》[5](以下简称《桥规》)承载能力极限状态荷载组合表达式为:
γ0Sud=γ0(1.2SGk+1.4SQlk+0.8×1.4SQjk)
(1)
式中:γ0为结构重要性系数,对应于设计安全等级一级、二级和三级分别取1.1、1.0、0.9;Sud为效应组合设计值;SGk为永久作用效应标准值;SQlk为汽车荷载效应(含汽车冲击力)的标准值;SQjk为人群荷载效应的标准值(本桥无人群荷载)。
现将边板、中板在设计汽车荷载作用下的承载能力极限状态荷载效应组合γ0Sud列于表1。
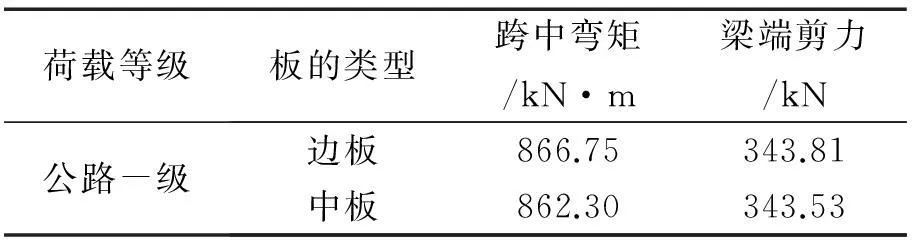
表1 设计汽车荷载作用下边板、中板荷载效应组合
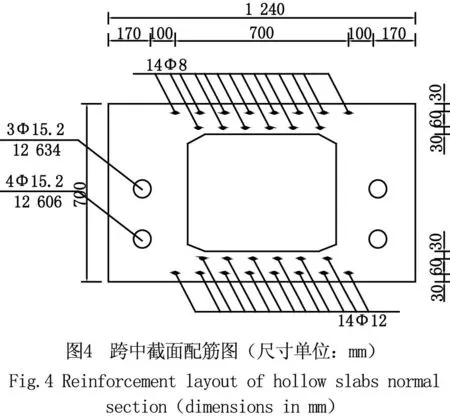
根据跨中截面配筋图如图4所示,计算得出边板、中板弯矩组合设计值Md分别为1 550.75、1 376.17 kN·m。计算结果表明,桥梁在设计汽车荷载作用下,边板、中板跨中正截面抗弯承载力均满足要求。
2.2 桥梁抗剪承载能力验算
为验算桥梁抗剪承载能力是否满足设计要求,现选取以下三个位置进行边板、中板斜截面抗剪承载力检算,为便于比较分析现将剪力组合设计值Vd与γ0的乘积、抗剪承载力Vu列于表2。
选取的三个位置分别为:(1)距支座中心h/2=350 mm处截面,x=5 950 mm;(2)距跨中位置x=5 150 mm(边板)或x=5 350 mm(中板)处截面(箍筋截面变化处);(3)距跨中位置x=4 050 mm处截面(箍筋截面变化处)。
计算结果表明,桥梁在设计汽车荷载作用下,边板、中板在不同位置处斜截面抗剪承载力均满足设计要求。
2.3 挠度验算
对于边板、中板,考虑长期效应的可变荷载引起的跨中挠度值分别为12.90、12.95 mm,考虑长期效应的一期恒载、二期恒载引起的跨中挠度分别为8.14、8.20 mm。
计算结果表明,边板、中板在公路-Ⅰ级汽车荷载短期效应作用下,桥梁跨中挠度均小于L/600,即21 mm,满足设计要求。
2.4 抗裂性验算
正截面抗裂性计算是对构件跨中截面混凝土的拉应力进行验算,预应力A类构件斜截面抗裂性验算是主拉应力控制,采用作用的短期效应组合,考虑温差作用。计算结果表明:该预应力混凝土空心板满足规范[6]对预应力A类构件抗裂性要求。
3 按典型限载车辆进行承载能力检算
李松辉[4]等应用桥梁限载简化分析程序,计算了2004年规范桥梁在受弯和受剪失效模式下的限载系数,进而选取原1985年规范五轴载重汽车为典型车辆荷载模型,并推算了相应的总重限值。

表2 边板、中板剪力组合设计值与抗剪承载力
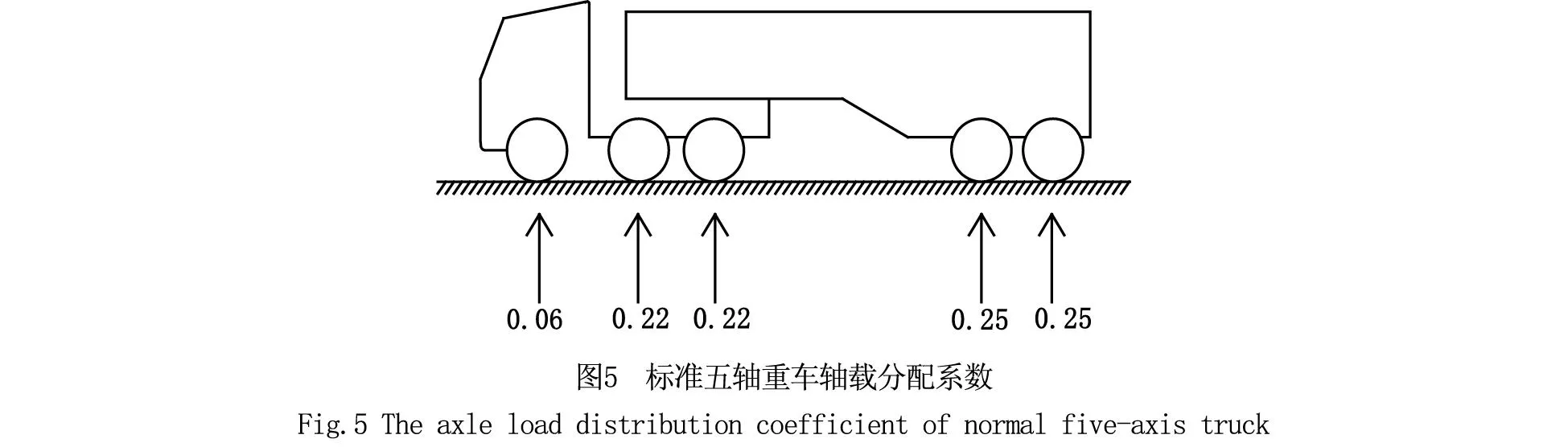
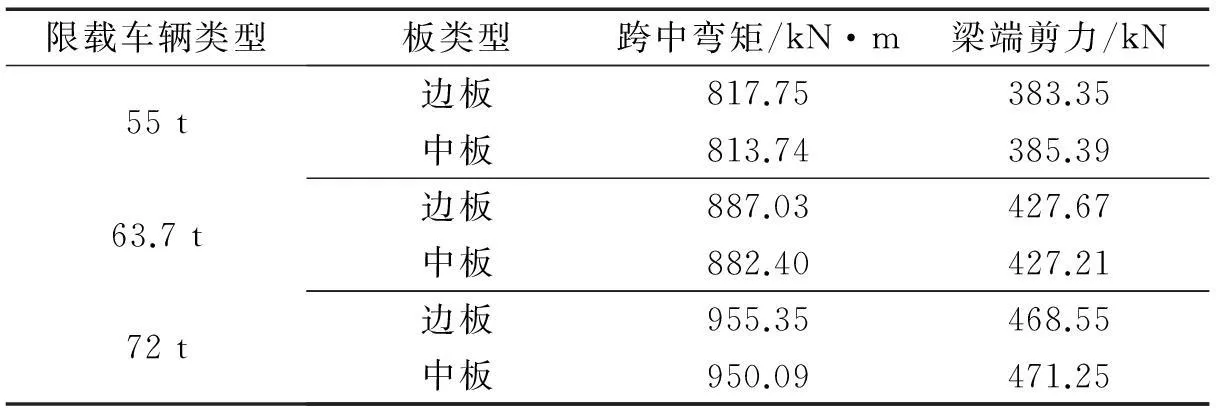
表3 边板、中板荷载效应组合

表4 边板、中板弯矩组合设计值与抗弯承载力
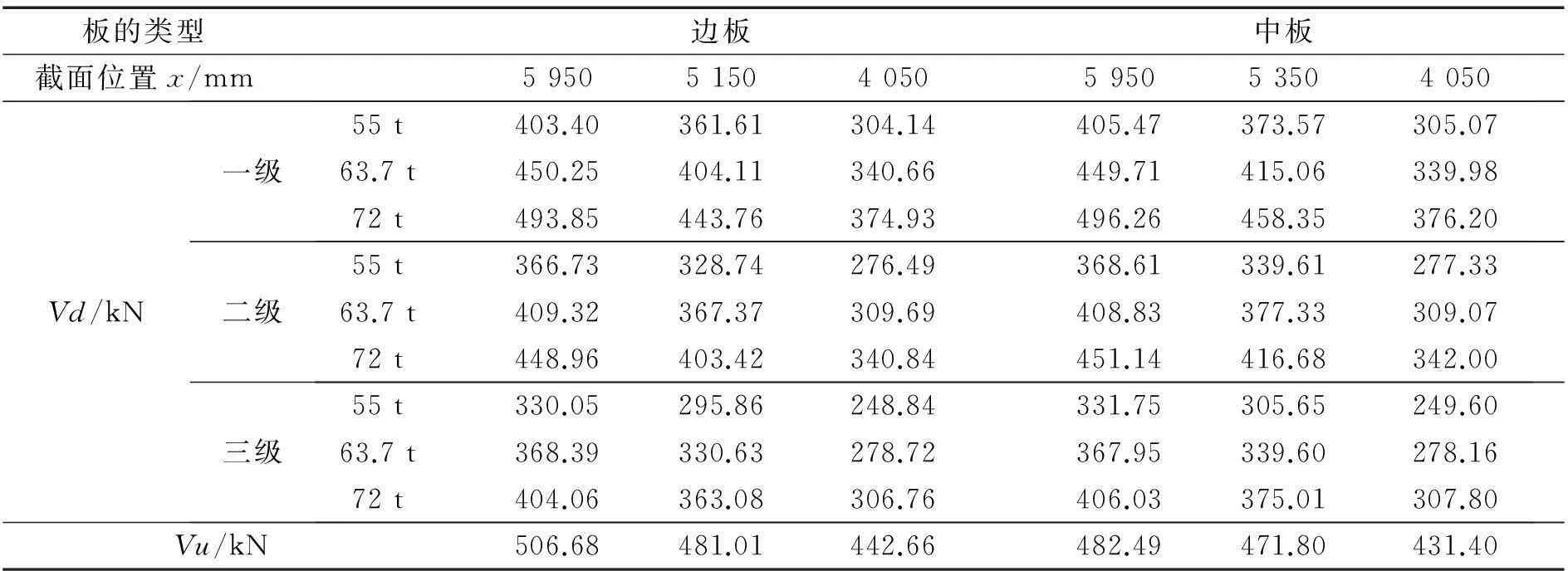
表5 边板、中板剪力组合设计值与抗剪承载力
其中,车辆轴载分配系数与1985年颁布的规范[7]中55 t车队重车的分配系数相同,典型车辆荷载模式见图5。经计算,对于公路-Ⅰ级简支梁桥,与安全等级一级、二级和三级对应五轴载重汽车总重限值分别为55、63.7和72 t。
3.1 典型限载车辆荷载作用下的荷载效应
根据计算得到的作用效应,按《桥规》承载能力极限状态荷载组合表达式(1),现将边板、中板在典型限载车辆作用下的荷载效应组合列于表3。
3.2 桥梁跨中截面抗弯承载能力验算
为验算桥梁在限载安全等级为一级、二级、三级时,不同典型限载车辆作用下抗弯承载能力是否满足设计要求,现将Md×γ0与Mu的计算数值列于表4。
计算结果表明,桥梁在一、二、三级安全限载等级下,分别选取55、63.7、72 t五轴载重汽车作为典型限载车辆荷载模式,γ0分别取1.1、1.0、0.9,正截面抗弯承载力均满足设计要求。
3.3 桥梁抗剪承载能力验算
为验算在典型限载车辆作用下桥梁抗剪承载能力,现选取以下三个位置进行边板、中板斜截面抗剪承载力检算,为便于比较分析,现将Vd与γ0的乘积、Vu列于表5。计算结果表明,中板在一级限载安全等级下,斜截面剪力组合效应超过抗剪承载力,除此之外,桥梁在一、二、三级安全限载等级下,边板、中板在不同位置处斜截面抗剪承载力均满足设计要求。

表6 正常使用阶段边板、中板挠度值

表7 空心板边缘混凝土法向拉应力
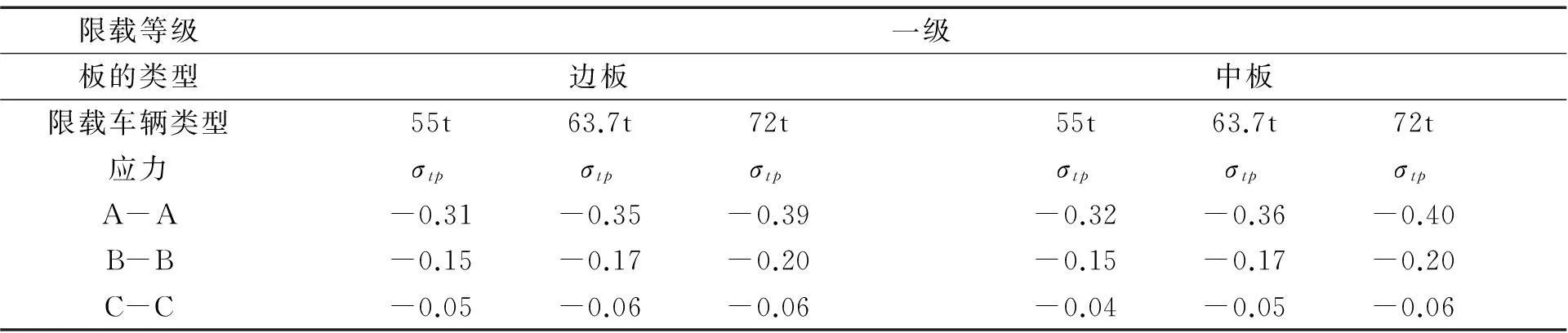
表8 空心板A-A、B-B、C-C纤维处主拉应力(单位:MPa)
3.4 挠度验算
为进一步验算空心板桥限载标准的安全性,对不同限载车辆进行跨中挠度检算。边板、中板在使用阶段的挠度值,按短期荷载效应组合计算,并考虑长期影响系数ηθ后,边板、中板在正常使用阶段的挠度值见表6。计算结果表明,不同限载安全等级下,边板、中板在典型限载车辆作用下桥梁跨中挠度均小于L/600,即21 mm,满足设计要求。
3.5 抗裂性验算
(1)正截面抗裂性验算。现将典型限载车辆作用下,边板、中板在短期、长期作用效应组合下,空心板抗裂验算边缘的混凝土法向拉应力σst、σlt列于表7。
表中σpc为扣除全部预应力损失后的预加力在构件抗裂验算边缘产生的预应力。由于桥梁在限载安全等级为二级、三级下,法向拉应力均小于一级限载安全等级下的主拉应力。因此,在不同限载安全等级下,典型限载车辆均满足σst-σpc<0.7ftk,σlt-σpc<0,符合《公预规》对A类构件的规定。
(2)斜截面抗裂性验算。分别计算支点截面A-A纤维(空洞顶面),B-B纤维(空心板换算截面重心轴),C-C纤维(空洞底面)处主拉应力,现将典型限载车辆作用下边板、中板在A-A、B-B、C-C纤维处主拉应力σtp列于表8。
计算结果表明,在一级限载安全等级下,不同限载车辆在边板、中板A-A、B-B、C-C纤维处的主拉应力均满足:σtp≤0.7ftk=0.7×2.65=1.855 MPa。限载安全等级为二级、三级时,主拉应力均小于一级限载安全等级下的主拉应力。因此,在不同典型限载车辆作用下,该预应力混凝土空心板满足《公预规》对预应力A类构件斜截面抗裂性要求。
3.6 限载标准安全性分析
计算结果表明:桥梁在一级安全限载等级下,55、63.7 t限载车辆荷载效应满足承载能力极限状态和正常使用极限状态要求,然而,通过比较55、63.7 t限载车辆与设计荷载产生的荷载效应,55 t限载车辆荷载效应与设计荷载效应更为接近,有较为合理的安全储备,因此在一级安全限载等级下选取55 t限载车辆限载较为合适。
72 t限载车辆荷载效应超过抗剪承载力设计值,因此在一级安全限载等级下不得采用72 t限载车辆限载。为安全起见,建议
72 t限载车辆在大件运输或超限审批时作为参考。
桥梁在二、三级安全限载等级下,55、63.7和72 t限载车辆荷载效应均满足承载能力极限状态和正常使用极限状态要求,然而通过比较三种限载车辆与设计荷载产生的荷载效应,二、三级安全限载等级下63.7、72 t限载车辆荷载效应与设计荷载效应更为接近,且有较为合理的安全储备,因此在二、三级安全限载等级下分别选取63.7、72 t限载车辆作为限载车辆较为合适。
4 结论
1)与安全等级一级和二级对应的55、63.7 t典型限载车辆模式,可以满足安全等级一级、二级和三级的承载能力要求。
2)与安全等级三级对应的72 t典型限载车辆,可以满足安全等级一级、二级和三级的正截面承载能力要求,但不能满足安全等级一级的斜截面抗剪承载力要求。
3)实际55、63.7 t限载车辆均可以作为公路-Ⅰ级桥梁在一级、二级和三级安全限载等级下的限载车辆,72 t限载车辆可以作为公路-Ⅰ级桥梁在二级和三级安全限载等级下的限载车辆,但在一级、二级和三级安全限载等级下分别选取55、63.7、72 t车辆限载较为合适。
参考文献:
[1]SIVAKUMAR B,MOSES F,et al.Legal truck loads and AASHTO legal loads for posting[R].Washington DC: Transportation Research Board,2007.
[2]GHOSN M.Development of truck weight regulations using bridge reliability model[J].Journal of Bridge Engineering,2000,5 (4):293-303.
[3]GHOSN M,MOSES F.Effect of changing truck weight regulations on us bridge network[J].Journal of Bridge Engineering,2000,5 (4) :304-310.
[4]李松辉.公路桥梁限载取值的可靠性分析模型研究[J].土木工程学报,2013,46(9):83-90.
[5]JTG D60-2004,公路桥涵设计通用规范[S].
[6]JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
[7]JTJ 023—1985,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
(责任编辑李军)
Security analysis on truck weight limits standard at highway bridges
AN Teng-fei,LI Song-hui,WANG Yan-wei
(Shandong Provincial Key Laboratory of Civil Engineering Disaster Prevention and Mitigation, Shandong University of Science and Technology, Shandong Qingdao 266590, China)
Abstract:Based on a pre-stressed concrete hollow slab bridge which located in Shandong province, the engineering security of truck weight limits model on highway bridges was verified systematically. Firstly, the bridge of carrying capacity is checked to verify the bridge weather meet the design requirements by according to the bridge design data and the design of truck weight of 2004 code .Then, the load effect and the deflection of mid-span of bridge in different typical truck of weight limits were calculated by according to the design of the truck lateral load patterns aiming at different safety classes ,respectively. And the data were compared with the design of truck weight to verify the engineering security of truck weight limits on highway bridges. The results indicate that, when the safety class of bridge truck weight limit were class one and class two, the corresponding typical truck of weight limits can satisfy the carrying capacity requirements of class one, class two and class three. when the safety class of bridge truck weight limit were class three, the corresponding typical truck of weight limits can satisfy the carrying capacity of normal section requirements of class one, class two and class three, but hardly satisfy the carrying capacity of cross section requirements of class one.
Key words:pre-stressed concrete hollow slab bridges; truck weight limits; typical truck of weight limits; limit states; security analysis
中图分类号:U411
文献标识码:A
文章编号:1673-9469(2016)01-0057-05
doi:10.3969/j.issn.1673-9469.2016.01.013
作者简介:潘腾飞(1988-),男,山东莱州人,硕士,主要从事桥梁安全鉴定、检测与加固方面的研究。
基金项目:中国博士后科学基金项目(2013T60681);山东省交通科技创新计划项目(2010Y01-2)
收稿日期:2015-09-29

