中美公路桥梁规范设计汽车荷载对比
闫保民, 李松辉
(山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛266590)
中美公路桥梁规范设计汽车荷载对比
闫保民, 李松辉
(山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛266590)
摘要:为对我国汽车荷载标准值在目前所处世界水平有较为客观的定位,同时,为我国将来公路桥梁新规范的修订建立基础。首先阐述中国新旧规范以及美国HL-93规范对设计汽车荷载的规定;其次以6、8、10、13、16、20、25、30 m不同跨径T型截面简支梁桥为基准,系统推算不同跨径T型简支梁桥在中美规范规定汽车荷载作用下的跨中弯矩和支点剪力;最后,系统对比分析荷载效应的绝对值与相对值。研究结果表明:与美国规范相比,中国规范相对来说较为保守,且不够直观,我国现行汽车荷载标准规范在国际上大致处于中等位置,在考虑与原规范联系性的基础上适当借鉴美国规范。
关键词:汽车荷载标准;跨中弯矩;支点剪力;荷载效应对比;中美
汽车荷载标准是公路桥梁设计重要依据之一,是设定安全可靠的鉴定荷载标准的首要前提。桥梁的安全性、经济性、耐久性与汽车荷载标准的合理性有着密不可分的关系,通过与国外汽车荷载标准的对比,找出自身的不足,从而予以改善。专家在研究不同国家之间荷载规范的基础上,得知我国现行规范的汽车荷载代表值中的标准值相当于美国规范中的汽车荷载值,均是依靠不同的分项系数来满足不同极限状态要求[1],且美国桥梁设计规范内容全面,在总体上运用了结构可靠度理论[2],故比较我国与美国AASHTO FRLD中的汽车荷载代表值之间的区别,比较具有实在意义。本文将我国规范与美国HL-93规范规定的汽车荷载分别作用到不同跨径简支梁桥上,计算最不利布载下的跨中弯矩值、支点剪力值,经过对比分析,研究二者的区别与联系。
1 中国汽车荷载标准
1.1 中国1985规范汽车荷载标准值
我国的1985规范汽车荷载标准采用车队模式,其中包括汽-10级、汽-15级、汽车-20级、汽车-超20级荷载标准[3],本文将汽-20级、汽-超20级进行对比分析,如图1所示。采用车队模式比较直观、容易理解,但是对于大型且较为复杂的桥梁动态加载来说,计算效率比较低,较为复杂。
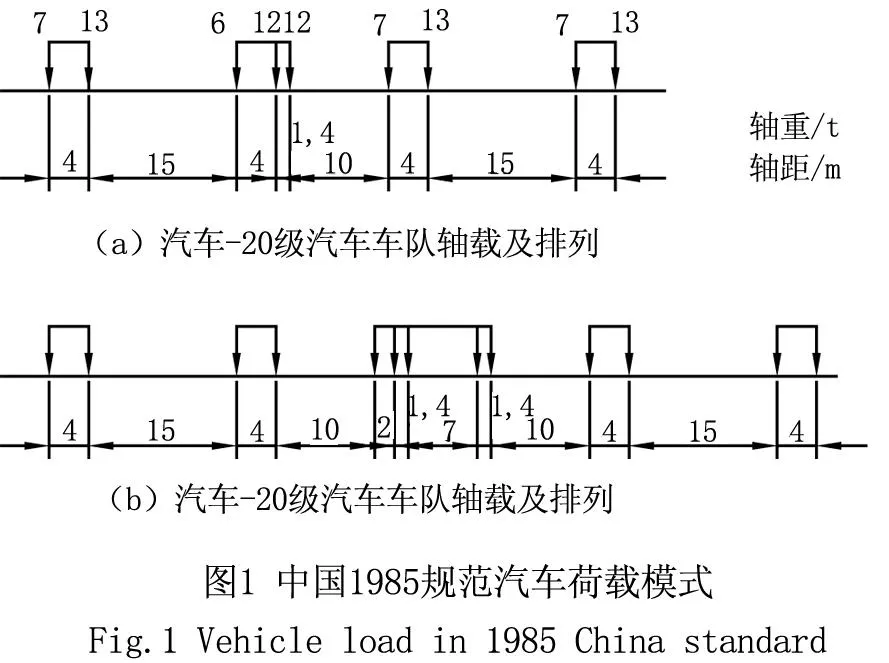
1.2 中国2004规范汽车荷载标准值
我国现行2004规范汽车荷载分为公路-I级和公路-II级两个等级,是在公路桥梁可靠度研究的基础上,由车道荷载和车辆荷载组成,车道荷载由均布荷载和一个集中力组成[4]。车道荷载与车辆荷载模式差别在于,前者适用于结构的整体计算,后者则适用于桥梁结构的局部加载,如涵洞、桥台和挡土墙土压力等的计算,且二者作用效果不可叠加。车道荷载模式如图2所示,我国现行规范(2004规范)关于汽车荷载标准值的规定,如下表1所示。
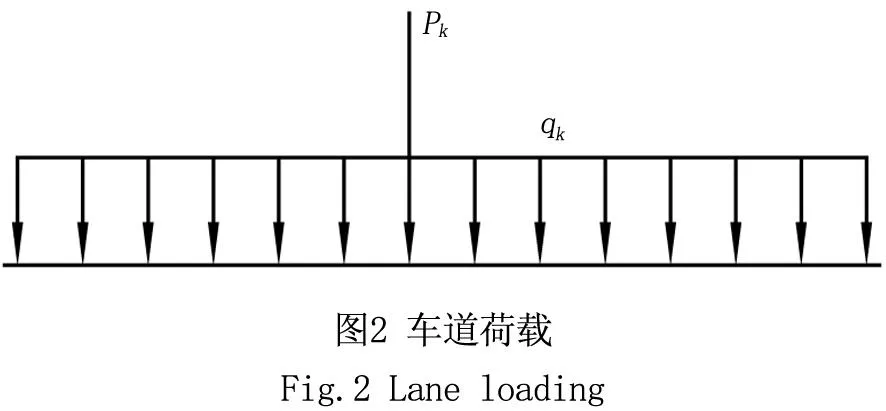
对于公路-I级汽车荷载,汽车荷载按表1取值;对于公路-II级汽车荷载,汽车荷载标准值按公路-I级相应的0.75倍计算。
1.3 实际运营汽车荷载
公路桥梁严格按照已有的汽车荷载标准进行建设,而实际运营的汽车荷载与标准汽车荷载之间往往存在差距,从而影响桥梁的安全性与耐久性。根据交通部颁布的《公路养护技术规范》[5],定期对桥梁承载能力及其使用条件进行检测必不可少。其中,美国AASHTO的《桥梁评估手册》中基于桥梁检测的桥梁负荷评级方法[6],值得我国学习与借鉴。
2 美国AASHTO汽车荷载标准
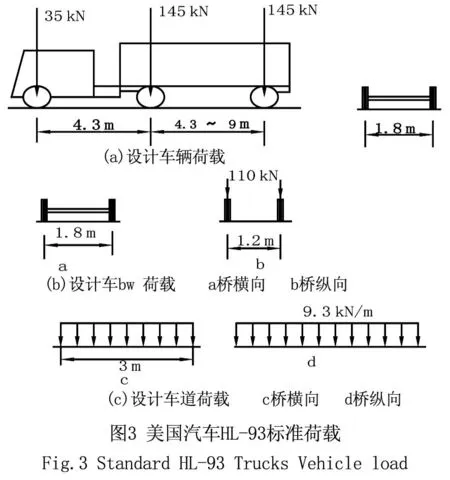
HL-93汽车荷载模型建立的背景在于对特殊车辆(如固体垃圾车和混凝土搅拌车)的研究,由于特殊车辆的重量一般大于法定荷载,且每次设计计算中单独考虑特殊车辆的作用较为麻烦,故在与特殊车辆产生的极端荷载效应相同的原则下,建立了HL-93汽车荷载模型。该规范包括三部分:设计车辆荷载,设计车队荷载,设计车道荷载[7],如图3所示。
图3(a)中车辆荷载驱动轴(145 kN)与后轴(145 kN)间距变化范围在4.39 m之间,从而产生极值效应。图3(b)设计车队荷载包括重为110 kN、间距为1.2 m的两辆车,车轮的横向间距1.8 m。图3(c)中的设计车道荷载包括分布于纵向的均布荷载,横向则假定为在3 m范围内的均匀分布。

表1 我国2004规范关于汽车荷载代表值的规定
AASHTO规定,产生极限荷载效应的组合包括:设计车队与设计车道荷载的组合效应;设计车辆荷载与设计车道荷载的组合效应;两辆设计车辆(两车间距至少15 m)效应的90%与设计车道荷载效应的90%组合,每辆汽车145 kN轴的距离取用4.3 m,用于计算处于均布荷载作用下反弯曲点之间的负弯矩和内部桥墩的反力作用。
3 中美汽车荷载冲击系数
冲击作用,即由于汽车荷载的动力因素,对桥梁内力或变形增大的影响。冲击作用影响复杂,对于钢筋混凝土桥,各国规范采用汽车荷载静力作用效应乘以系数(Hμ)的方式来表达。
中国1985规范规定:冲击系数μ作为跨径的函数,当跨径L≤5m时,μ=0.3;当L≥45m时,μ=0。中国2004规范规定:冲击系数作为桥梁基频的函数,当f<1.5 Hz时,μ=0.05;当1.5 Hz≤f≤14 Hz时,μ=0.176 7 lnf-0.015 7;当f>14 Hz时,μ=0.45。
结合内插法计算得出不同规范汽车荷载对不同跨径简支梁桥的冲击系数,如表2所示。事实上,造成冲击的原因主要在于三点:车轮不圆,路面不平,车辆发动机的抖动[8]。结果表明,对于中小跨径桥梁,随着跨径的增大,冲击系数呈减小趋势,且中国比美国规范减小的速度要快,可见我国公路桥梁在路面平整度上有待于提高。关于我国规范规定的冲击系数取值有待进一步研究与探讨。
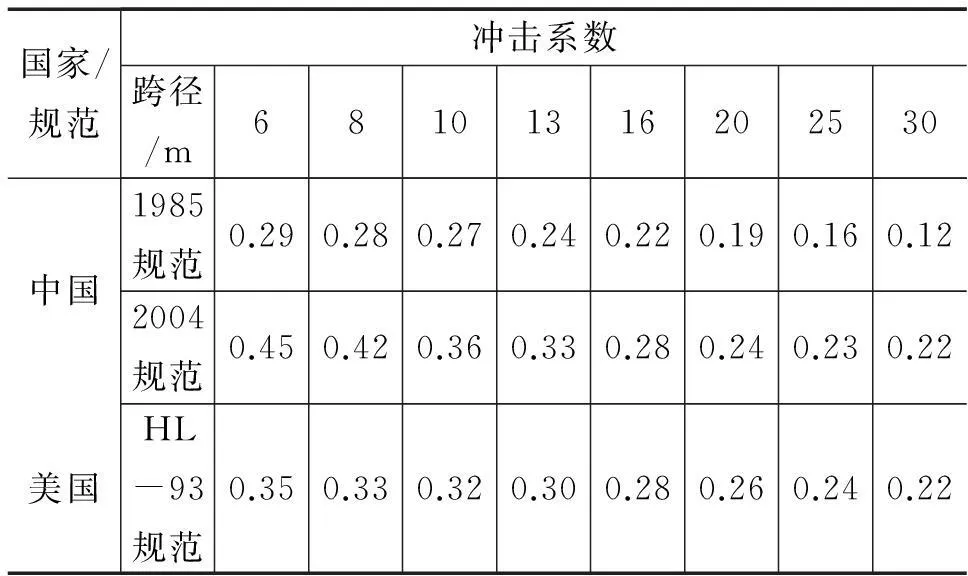
表2 中美规范不同跨径简支梁桥汽车荷载冲击系取值
4 中美汽车荷载标准值效应对比
4.1 汽车荷载效应计算
根据对各跨径简支梁跨中弯矩及支点剪力影响线进行最不利荷载布置计算分析,并考虑冲击系数的影响,得到荷载效应值,详见图4。
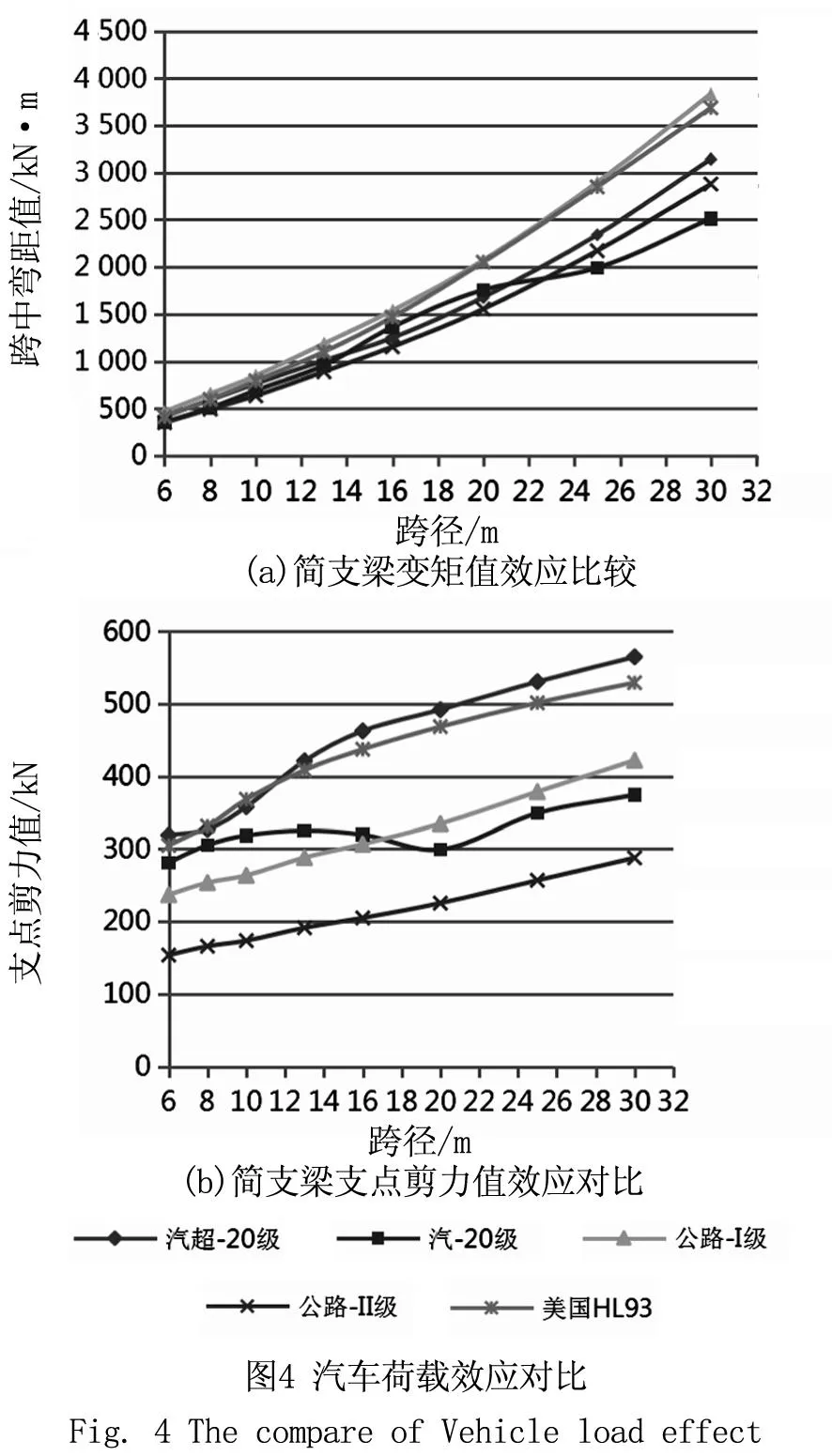
4.2中美规范汽车荷载效应比值
为了更加清楚直观的对比中美规范汽车荷载效应,现将跨中弯矩效应比值、支点剪力效应比值分别以散点图的形式表现出来,从而观察1985规范与2004规范在美国规范(纵轴为100%)处的波动范围,见图5。
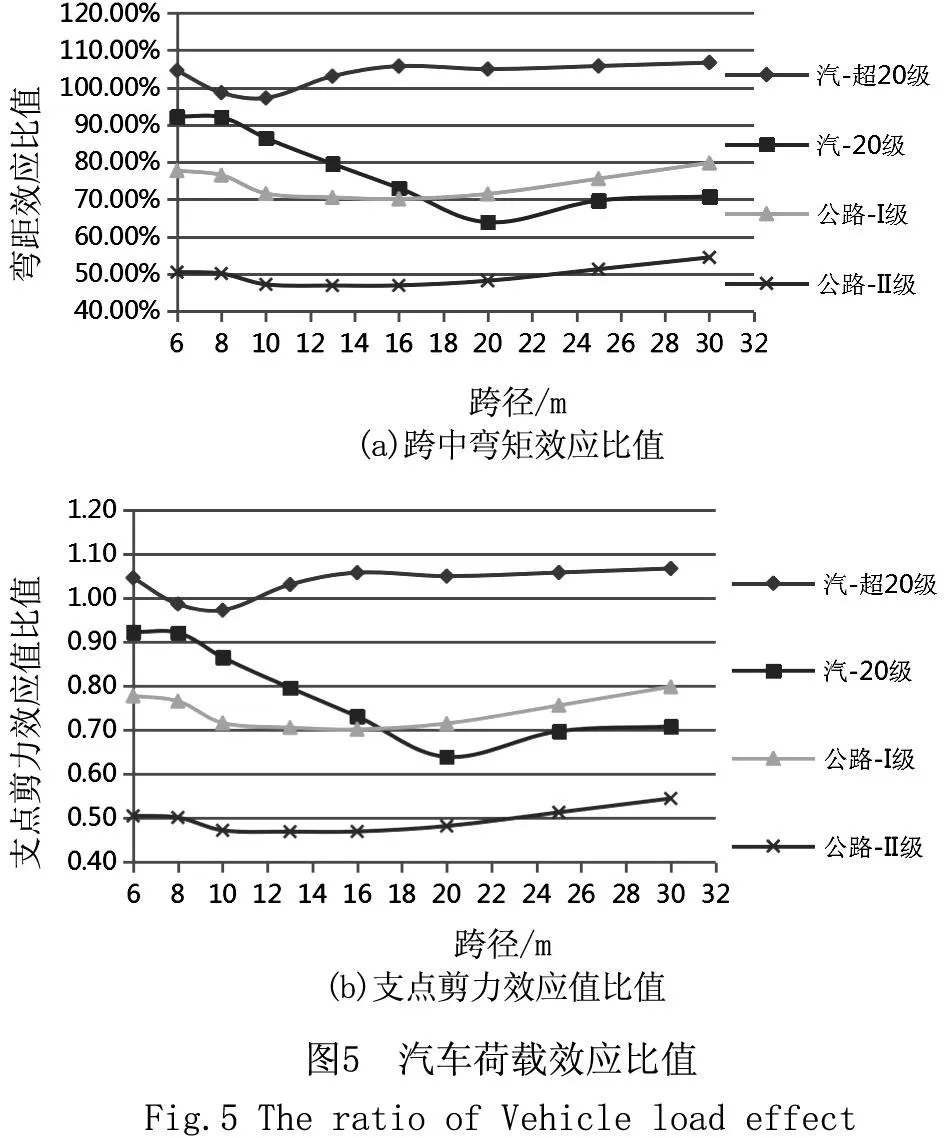
4.3 中美两国荷载效应对比分析
通过最不利布载方式,初步计算出中美规范汽车荷载标准值效应,分析结果表明:
(1)从图4中可以看出,随着跨径的增加,中国与美国桥梁汽车荷载在简支梁上产生的效应值总体趋势相同,但是荷载效应值的大小差异较为明显,美国规范较我国1985规范的公路-I级产生的弯矩效应值较为接近,随着桥梁跨径的增大,跨径为30 m时,中国比美国大约14.7%,且随着跨径的增大,差距逐渐增大。其中,汽-20级产生的内力最小[9]。
(2)美国规范产生的剪力荷载效应值与汽-超20级较为接近,简支梁跨径为8~12 m之间,美国小于后者,随着跨径增大,前者小于后者约4%~6%,且差距逐渐趋于稳定。我国现行2004规范中的公路-I、公路-II级相比美国,简支梁支点剪力效应值则差距较大,前者比后者小约15%~20%,这与我国治超水平可能有较大关系[10]。
(3)从弯矩组合效应值来看,相比美国规范,中国规范相对比较安全,与公路-I级相差不大,也证明我国现行规范相对比较合理,但是从剪力组合效应值来看,美国规范与汽-超20级较为接近,但是公路-I级比美国规范小约20%~30%,可见,在汽车荷载设计值上,美国规范优于中国现行规范。
(4)已知中国公路-I级相比1985规范的汽车荷载模型来说,比较简单,计算起来比较方便,但是相对不如1985规范、美国规范来的直观。因为后者与汽车轴距、轴重都有关系。
5 结论
中国桥梁规范中的设计汽车荷载相比美国规范来说,比较保守。从弯矩效应值对比可知,我国公路-I级与美国规范比较接近,我国现行规范在国际上处于中等行列。从剪力效应值对比中发现,我国的汽车-超20级与HL-93规范较为接近,可知我国的1985规范以轴力形式展现的汽车荷载模型具有一定的代表性,这是我国2004规范所不具备的。
参考文献:
[1]张喜刚.公路桥梁汽车荷载标准研究[M].北京: 人民交通出版社,2014.
[2]张 磊,金 菊,宋娃丽.中美规范公路混凝土桥梁设计的分析与比较[J].河北工业大学学报,2011,40(6):99-102.
[3]JTJ 021-85.公路桥涵设计通用规范[S].
[4]JTG D60-2004.公路桥涵设计通用规范[S].
[5]JTG H10-2009.公路养护技术规范[S].
[6]AASHTO LRFD.The Manual for Bridge Evaluation,Second Edition[S].
[7]AASHTO LRFD.Bridge Design Specifications,SI Units Third Edition[S].
[8]张士铎.中美两国公路桥梁标准荷载内力计算的分析与对比[J].重庆交通学院学报,1984,10(3): 1-12.
[9]党 栋.公路桥梁设计荷载及其组合研究[D].西安: 长安大学,2012.
[10]赵 飞.中美超重车辆认定标准对比[J].河北工程大学学报: 自然科学版,2015, 32(4):58-62.
(责任编辑王利君)
Study of vehicle load between China and America in bridge design specification
YAN Bao-min, LI Song-hui
(Key Laboratory of Civil Engineering Disaster Prevention and Mitigation, Shandong University of Science and Technology, Shandong Qingdao 266590, China)
Abstract:In order to have a more objective position on the world level of the standard value of vehicle load in China and make a foundation for the revision of the resent standard of Highway Bridge. This paper has explained the China’s new and old code and the United States HL-93 specification for the design of vehicle loads, then take 6, 8, 10, 13,16, 20,30 meters long span bridge with T shaped beam for example, to make a systematic calculates of mid-span moment and shear force at supporting point of T-shaped beam, which is under the action of vehicle load in the Chinese and American Codes. In the end, the absolute value and the relative value of the load effect are analyzed systematically. The results show that: compared with the United States, the Chinese standard is relatively conservative and not intuitive, China’s current vehicle load standard specification in the international is roughly in the middle position, considering the contact with the original specification, the appropriate reference to the United States.
Key words:characteristic value of vehicle load; mid-span moment; shear force at supporting point; comparison of load effect;
中图分类号:U447
文献标识码:A
文章编号:1673-9469(2016)01-0053-04
doi:10.3969/j.issn.1673-9469.2016.01.012
作者简介:闫保民(1989-),女,山东菏泽人,硕士,主要从事桥梁检测与安全性评估方面的研究。
基金项目:山东省交通科技创新计划项目(2010Y01-2);旧桥检测与加固技术交通行业重点实验室(北京)开放课题(Jqkf2011-14)
收稿日期:2015-11-20

