厚壁钢桥墩的超低周疲劳裂纹萌生寿命预测
池世粮,高圣彬
(上海交通大学 船舶海洋与建筑工程学院,上海 200240)
厚壁钢桥墩的超低周疲劳裂纹萌生寿命预测
池世粮,高圣彬
(上海交通大学 船舶海洋与建筑工程学院,上海 200240)
摘要:为获得厚壁钢桥墩的超低周疲劳裂纹萌生寿命,对多组厚壁钢桥墩进行数值模拟分析。采用钢材的混合强化模型预测厚壁钢桥墩在三种不同往复荷载作用下的滞回性能,并分别使用Ge模型中的局部损伤法与非局部损伤法得到不同网格尺寸下的钢桥墩超低周疲劳裂纹萌生寿命,然后使用Ge模型对厚壁钢桥墩的疲劳裂纹萌生寿命影响因素(翼缘宽厚比、试件通用长细比等)进行参数化分析。研究结果表明:混合强化模型能准确预测厚壁钢桥墩的滞回性能;Ge模型中的非局部损伤法能准确预测厚壁钢桥墩的超低周疲劳裂纹萌生寿命。最后基于裂纹萌生寿命的参数化分析结果,提出了预测钢桥墩超低周疲劳裂纹萌生寿命的经验公式。
关键词:桥梁工程; 钢桥墩;参数化分析; Ge模型;超低周疲劳;疲劳裂纹萌生寿命
在强震作用下,钢桥墩一般通过非弹性往复大变形来耗散地震能量,从而在桥墩与基础连接处产生很大的塑性应变,该应变通常可以达到钢板屈服应变的数倍以上,并在较少的循环次数下(小于100次)产生疲劳裂纹,从而在局部失稳和整体失稳之前造成钢桥墩承载力突然下降,该类问题被称为超低周疲劳问题[1-4]。其破坏性质属于典型的延性断裂,延性断裂的过程包括延性裂纹萌生、扩展、破坏等[5-8]。在厚壁钢桥墩的抗震设计中,超低周疲劳破坏是一个需要考虑的重要破坏形式。对于受到多种几何参数影响的钢桥墩来说,试验存在工作量大、耗时长、费用昂贵等问题,因此数值模拟手段成为解决该问题的重要替代方法[9]。文献[4]分别采用已校准的微观断裂判据退化有塑性应变模型和循环空穴扩张模型对方钢管柱与H形钢梁焊接节点进行超低周疲劳断裂预测;文献[10]采用循环空穴扩张模型对钢结构的梁柱节点进行超低周疲劳寿命预测;文献[11]提出基于塑性应变幅的损伤累积模型(以下简称为Ge模型)。国内外对厚壁钢桥墩的裂纹萌生寿命与翼缘宽厚比和试件通用长细比之间的关系研究较少,通过数值模拟方法研究钢桥墩裂纹萌生寿命与二者之间的关系是一个新的尝试。本文首先采用Ge模型对三组钢桥墩试验试件在三种不同往复荷载作用下的裂纹萌生寿命进行预测,并推出预测钢桥墩裂纹萌生寿命的经验公式,以供工程设计参考。
1有限元分析方法验证
1.1试验试件基本参数
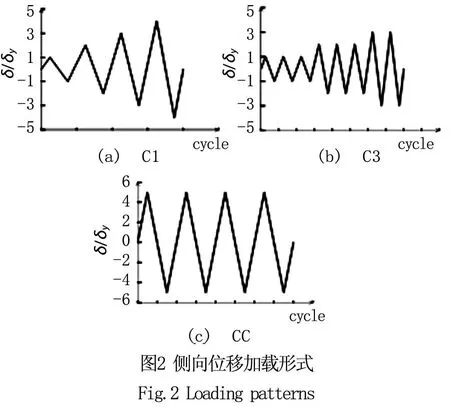
考虑往复荷载加载形式、翼缘宽厚比、试件通用长细比等多种因素,对 9个钢桥墩试件的裂纹萌生寿命进行试验与数值模拟结果的对比分析。试件的立面和横截面如图1所示,钢桥墩的几何尺寸如表1所示。侧向位移采用图2所示的C1、C3和CC三种加载形式。C1指每一个侧向位移值对应一次往复加载,一次往复加载结束后侧向位移幅值增加;C3指每一个侧向位移值对应三次往复加载,每三次往复加载结束后侧向位移的幅值增加;CC指侧向位移加载过程中位移的幅值保持不变。
根据文献[12]的试验,钢桥墩裂纹产生的判定依据为钢板表面出现肉眼可见的1~2 mm长度的裂纹。试验结果表明,试件的裂纹萌生点都产生于
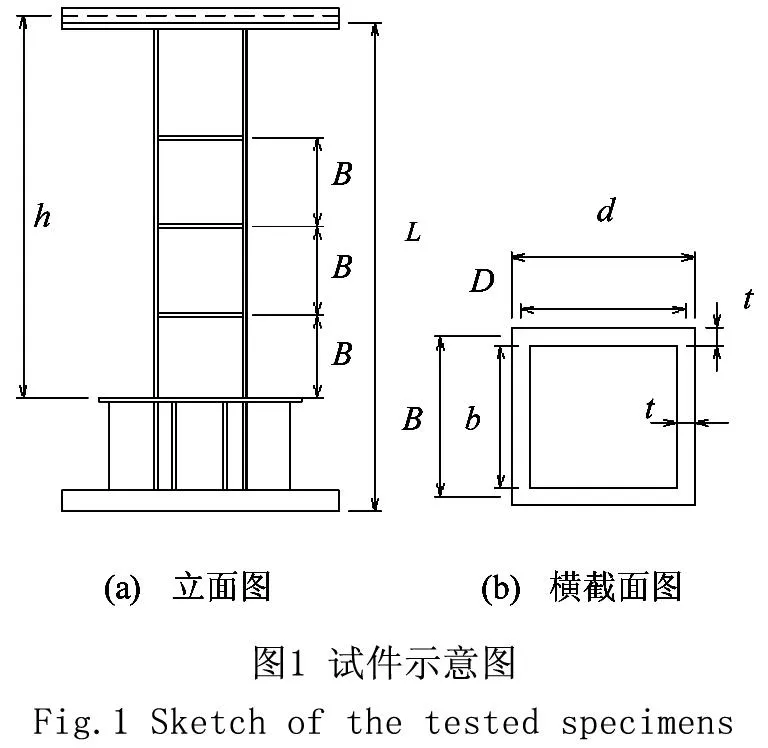
表1 试件的几何尺寸
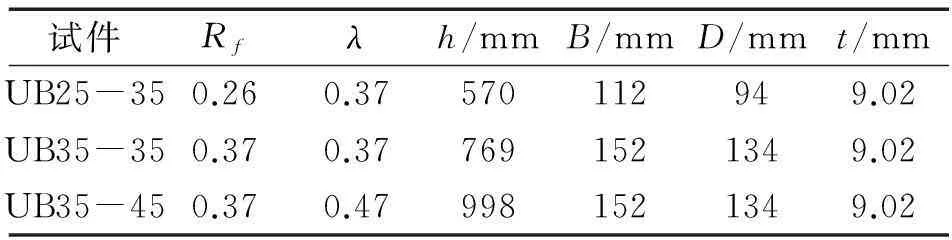
试件Rfλh/mmB/mmD/mmt/mmUB25-350.260.37570112949.02UB35-350.370.377691521349.02UB35-450.370.479981521349.02
注:UB指无加劲助的箱形截面;Rr为翼缘宽厚比;λ为试件通用长细比;h为试件高度;B为翼缘宽度;D为腹板净宽度;t为翼缘和腹板厚度。
桥墩与基础的连接部位,并且位于翼缘与腹板交接处,随后裂纹向两侧发展,全面进入翼缘和腹板,导致钢桥墩的承载力明显下降。大多数的试件都是在裂纹萌生点产生以后才出现局部失稳,少数试件甚至在局部失稳出现前已经因超低周疲劳而破坏。
1.2有限元建模
使用ABAQUS有限元分析软件建立钢桥墩的三维分析模型,根据荷载以及结构形式的对称性,只需进行1/2建模。在建模过程中不考虑焊缝,因为根据文献[11]的研究成果发现,没有考虑焊缝的情况与考虑焊缝相比计算结果比较接近,未考虑焊缝的预测结果更加偏于安全,而且如果要模拟焊缝会导致网格的划分更密,从而会极大地增加单元数和计算时间。
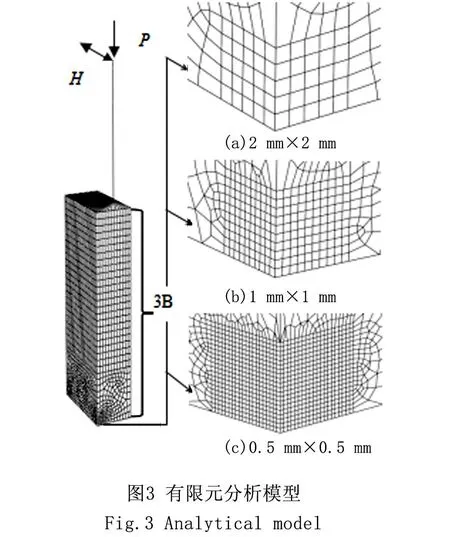
如图3所示,桥墩下部3B区域内的钢板采用壳单元,3B以上的区域采用梁单元,梁单元与壳单元之间的连接部分使用刚性梁单元,以确保连接处的截面满足平截面假定。在靠近桥墩根部的应变集中区域,需细分有限元网格。为了探讨网格尺寸对裂纹萌生寿命预测结果的影响,对钢桥墩角部10 mm×10 mm区域采用如图3所示的三种不同网格尺寸划分方式(2 mm×2 mm,1 mm×1 mm,0.5 mm×0.5 mm)。假定钢桥墩底部与基础之间固结,在桥墩的顶部施加0.1Py的竖向轴压力后,再施加侧向往复位移,其中Py为桥墩的轴心受压屈服荷载值。
本文中,钢材本构模型使用文献[13]中的Lemaitre-Chaboch混合强化模型,该模型同时具有等向强化模型和随动强化模型的特征,能够考虑包辛格效应以及弹性应变范围扩大等因素,反映钢材在往复荷载作用下的循环塑性流动情况。具体的钢材参数值如表2所示,各个参数的物理意义参见文献[14]。
1.3 计算结果与试验结果的比较
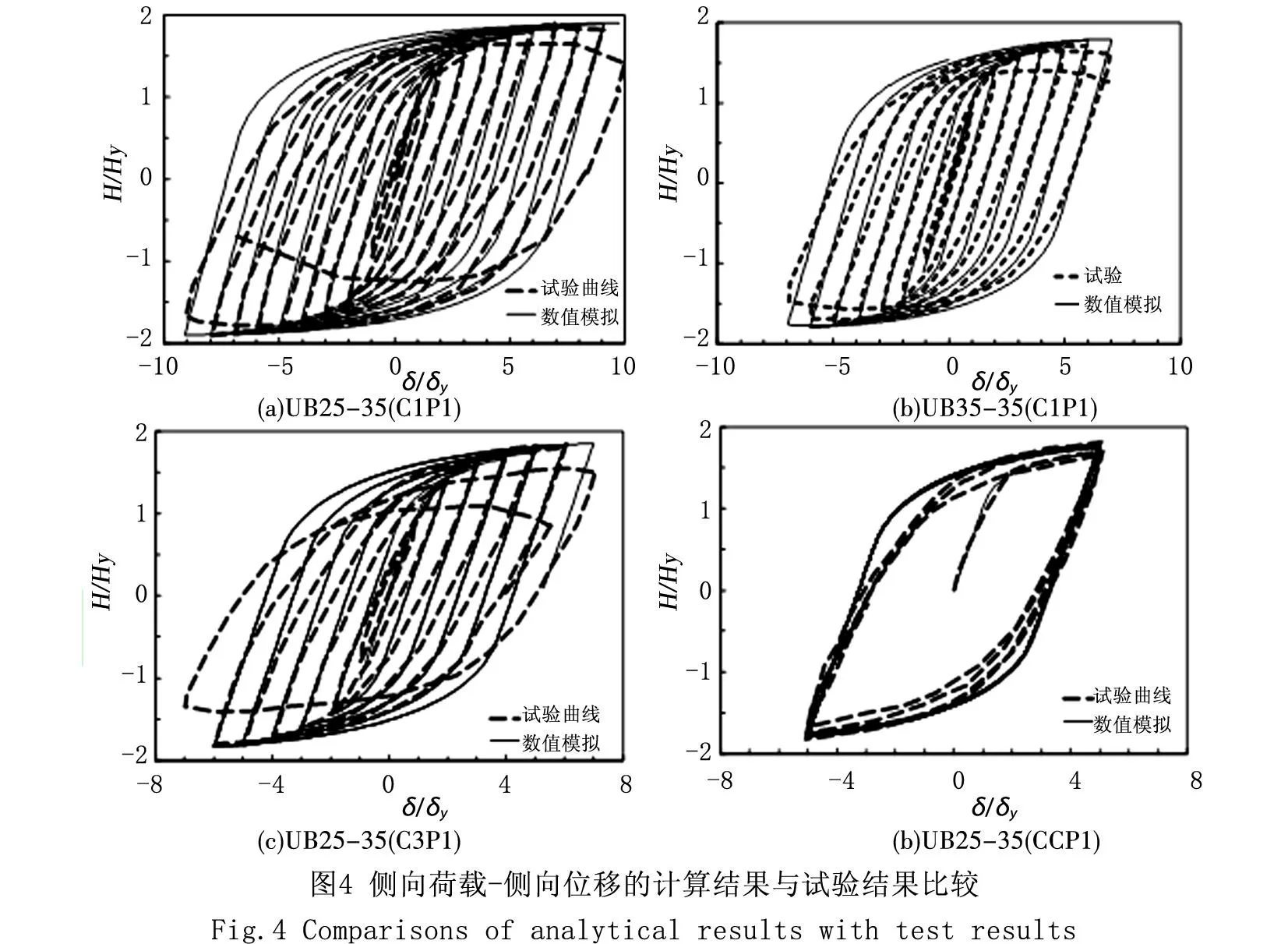
图4为无量纲化后的侧向荷载-侧向位移滞回曲线比较,其中和分别为试件的侧向屈服荷载与侧向屈服位移。可以看出,采用钢材混合强化模型所预测的荷载-位移曲线与试验结果吻合良好。图4(a)和4(c)中试验曲线的承载力最后出现显著下降是因为试件发生超低周疲劳破坏,而数值模拟分析不能考虑因超低周疲劳破坏产生的承载力下降影响。总体来说,本文采用的有限元分析方法能够准确预测厚壁钢桥墩在超低周疲劳破坏出现之前的滞回性能。
2 基于Ge模型的裂纹萌生寿命预测
本节分别采用Ge模型中的局部损伤法和非局部损伤法对厚壁钢桥墩在不同加载形式以及不同网格尺寸下的裂纹萌生寿命进行预测,并通过预测结果与试验结果的比较,确定合适的裂纹萌生寿命预测方法。
改变现有的以理论讲授为主,实验仿真为辅的教学方式.在课堂上,以教师问题引导为主,学生自学和回答问题为辅的互动教学模式,提高学生学习的主动性.教师利用专业的仿真软件,根据课程内容的理论分析,进行动态仿真分析,并以实验图片与理论分析对比,加深学生对课本内容的理解,也让学生学会了专业仿真软件的使用方法.不仅可以加深理论知识的学习,而且可以培养学生利用现有理论进行设计仿真的能力.
表2 钢材参数表
Tab.2 Material parameters of steel

σ0/MPaσ∞/MPabC1/MPaY1C2/MPaY2C3/MPaY3C4/MPaY4380211.279201756431101248935136723
2.1 Ge模型中的局部损伤法
Ge 模型中的局部损伤法根据式(1)所计算的损伤累积指标来判断裂纹是否萌生。
D=C′∑(εpr)m
(1)
式中,εpr为每半个周期的塑性应变幅;C′和m是材料常数(C′=9.69,m=1.86)。当D值达到1.0时,表示钢桥墩中出现裂纹,钢桥墩中最易出现裂纹的位置是在桥墩根部附近的腹板与翼缘交接处。为了减小计算工作量,在网格加密区内只选取应变最集中的一个单元进行D值计算。在不同的网格尺寸下,应变幅的幅值有所不同,但不论在何种加载形式下,0.5 mm×0.5 mm网格细分方式的单元应变幅值总是大于1 mm×1 mm和2 mm×2 mm,这主要是因为在0.5 mm×0.5 mm的网格细分方式下,计算单元更加靠近角部,应变幅更大。由于裂纹萌生寿命的判定与塑性应变幅密切相关,因此裂纹萌生寿命对网格尺寸具有很大的敏感性。采用局部损伤法预测的裂纹萌生寿命结果如表3所示,可以看出采用2 mm×2 mm网格细分方式的局部损伤法,能较好地预测厚壁钢桥墩在不同加载形式下的裂纹萌生寿命。
2.2 Ge模型中的非局部损伤法
非局部损伤法是指选定塑性应变集中区内的一小块区域作为D值计算的范围,采用该区域内的带权函数平均塑性应变作为总的塑性应变来计算D值。裂纹平均塑性应变计算公式以及Ge 模型中的损伤累积指标计算公式如式(2)所示,其中Ω表示计算范围,详见文献[15]。
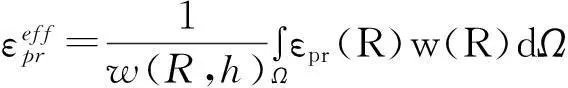
(2)
式(2)中,选用的权函数公式如式(3)所示:
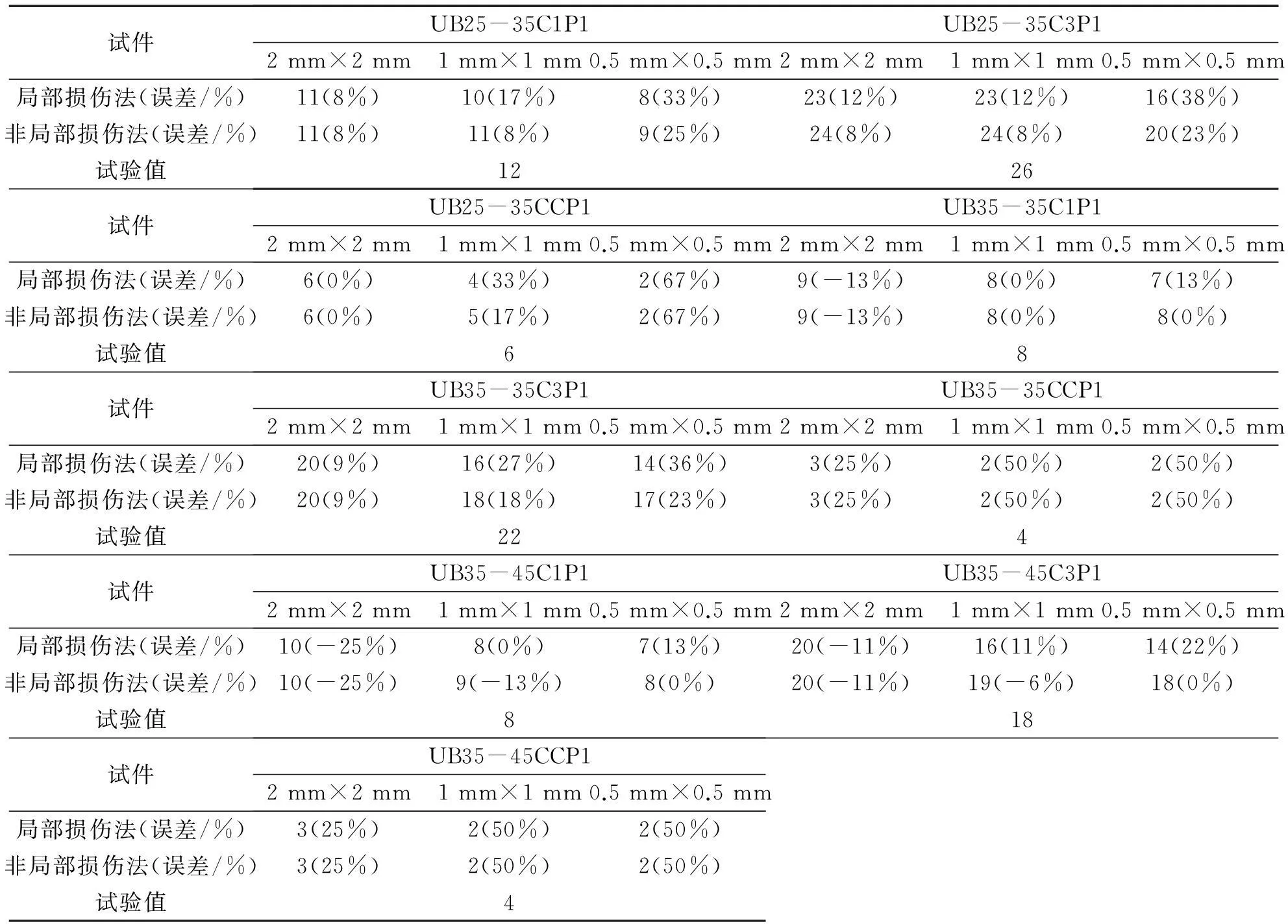
表3 裂纹萌生寿命的计算结果与试验结果比较
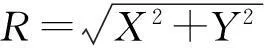
(3)
上式中,X与Y分别为所选取网格中心与根部腹板和翼缘交接处在X方向及Y方向的距离。权函数需满足以下三个条件:在计算范围Ω内,w(R)≥0。计算范围域Ω外,令w(R)=0;在计算范围内,随着R值的增大,w(R)值减小;当h时,w(R)就成为峰值点,此时非局部损伤法转变为局部损伤法[16-17]。
根据文献[18]的研究,非局部损伤法的计算范围以4 mm×4 mm为宜,网格尺寸通常要小于2 mm×2 mm。采用非局部损伤法得到的损伤值结果与采用局部损伤法的结果相似,但非局部损伤法的损伤值普遍低于局部损伤法。由于非局部损伤法计算的塑性应变区域大于局部损伤法,得到的计算结果具有更好的代表性。从网格尺寸的影响来看,和局部损伤法的计算结果一样,相同半周期所对应的损伤值是0.5 mm×0.5 mm大于1 mm×1 mm和2 mm×2 mm,显示出非局部损伤法对于网格尺寸也具有敏感性。
裂纹萌生寿命的计算结果如表3所示。为了便于比较,将非局部损伤法与局部损伤法得到的结果以及试验结果三者放在一起。从表中可以看出,与局部损伤法一样,由非局部损伤法得到的裂纹萌生寿命对网格尺寸大小也具有敏感性,裂纹萌生寿命预测结果是2 mm×2 mm大于1 mm×1 mm和0.5 mm×0.5 mm。在网格尺寸为2 mm×2 mm的情况下,局部损伤法与非局部损伤法的裂纹萌生寿命预测结果并没有明显区别,然而由0.5 mm×0.5 mm和1 mm×1 mm的计算结果可以看出,二者的裂纹萌生寿命预测存在一定差距,非局部损伤法的计算值略大于局部损伤法的计算值。与局部损伤法相比,非局部损伤法得到的结果中,由网格尺寸导致的裂纹萌生寿命之间的差异减小,表明非局部损伤法的预测方式更加稳定、可靠,对于网格尺寸的敏感程度下降,比较适用于实际的裂纹萌生寿命预测。
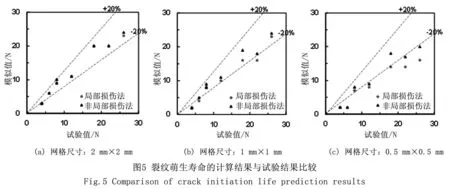
图5将局部损伤法与非局部损伤法得到的计算结果与试验结果进行比较,虚线表示±20%的误差线。可以看到,当网格尺寸为2 mm×2 mm时,无论是由局部损伤法还是非局部损伤法得到的计算值,基本位于±20%的误差线以内。从网格尺寸的敏感性来看,非局部损伤法明显优于局部损伤法,尤其是网格尺寸为0.5 mm×0.5 mm时对应的局部损伤法,许多数据都已超出±20%的误差线。从误差大小、有限元模型计算量以及对网格尺寸的敏感性等角度综合考虑,认为网格尺寸为2 mm×2 mm的非局部损伤法为裂纹萌生寿命预测的最优计算方法。
3 裂纹萌生寿命影响的参数化分析
根据前述计算结果与试验结果的比较可知,钢材混合强化模型和Ge模型中网格尺寸为2 mm×2 mm非局部损伤法适用于预测厚壁钢桥墩的超低周疲劳裂纹萌生寿命。从前面的试验数据可以看出,厚壁钢桥墩的裂纹萌生寿命与翼缘宽厚比和通用长细比之间存在一定的规律。为了进一步获得具体的定量公式,本节选取Q345钢材作为建模材料,针对不同翼缘宽厚比与试件通用长细比的钢桥墩进行参数化分析,进一步探讨裂纹萌生寿命与上述两参数之间的关系。翼缘宽厚比Rf的变化范围为0.20~0.45,试件通用长细比λ的变化范围为0.25~0.50。在考虑轴压比为0.1的情况下,对不同试件在三种加载形式下预测的裂纹萌生寿命分别见表4~表6。从表中可以看出,在翼缘宽厚比相同的情况下,随着通用长细比的增大,裂纹萌生寿命基本保持不变。在试件通用长细比相同的情况下,除了UB45-50试件外,裂纹萌生寿命随着翼缘宽厚比的增大而减小。其中UB45-50试件的壁厚较小,出现了因局部屈曲引起的塑性应变幅增量减小,从而导致预测的超低周疲劳裂纹寿命略微偏大。为了定量预测钢桥墩的裂纹萌生寿命,采取曲线拟合方法对计算结果进行数据处理,得到在不同加载形式下的疲劳裂纹萌生寿命预测公式如下:
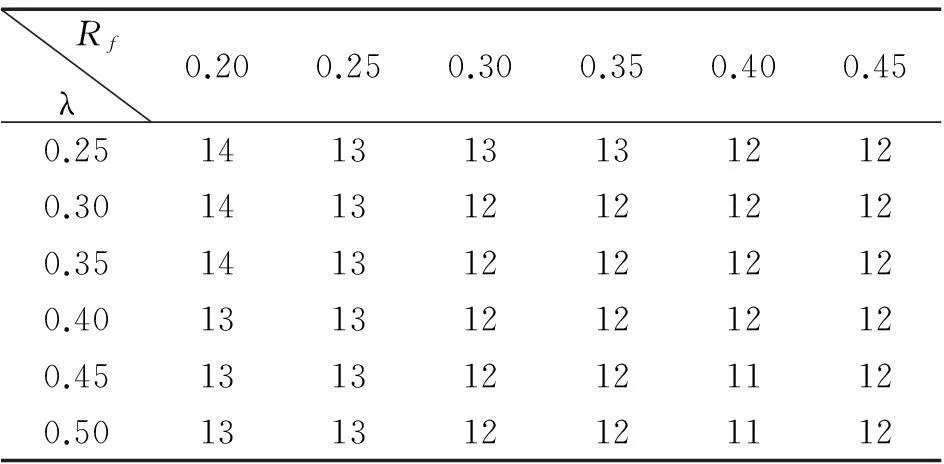
表4 系列桥墩在C1P1加载形式下的裂纹萌生寿命
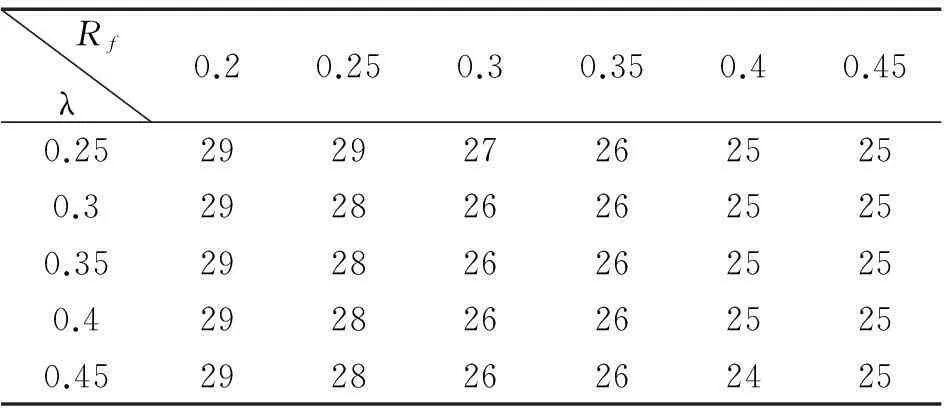
表5 系列桥墩在C3P1加载形式下的裂缝萌生寿命
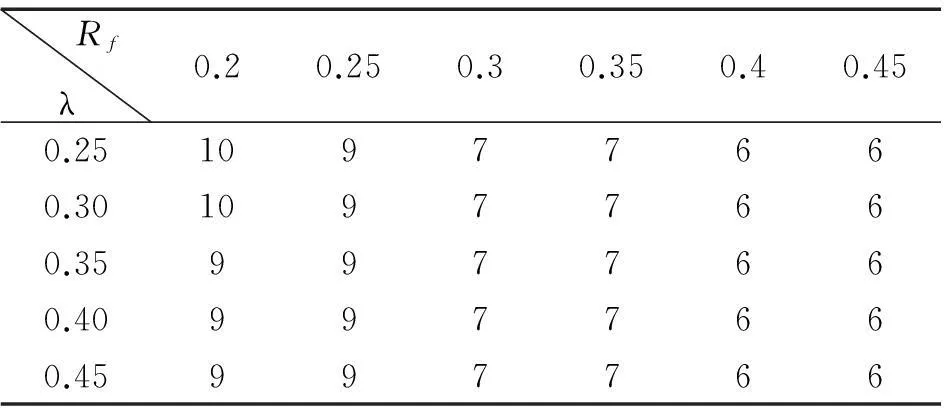
表6 系列桥墩在CCP1加载形式下的裂纹萌生寿命
C1P1加载形式:
(4)
C3P1加载形式:
(5)
CCP1加载形式:
(6)
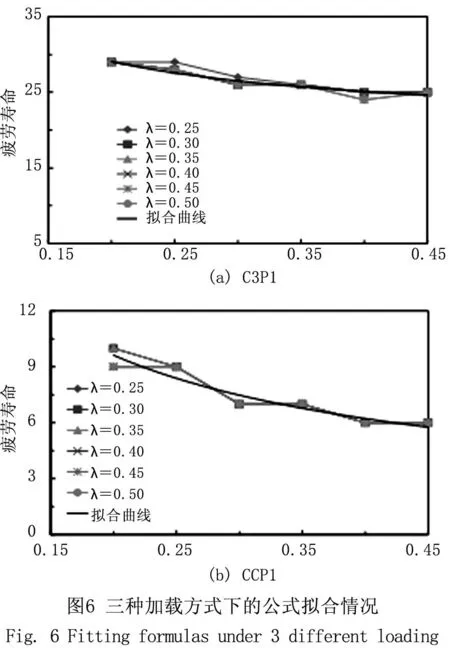
部分加载形式下拟合曲线的具体情况如图6所示,可以看出在多种往复荷载作用下,拟合公式都能较好地预测钢桥墩的超低周疲劳裂纹萌生寿命。
4 结论
1)由数值模拟得到的侧向荷载-侧向位移曲线和试验曲线吻合良好,表明Lemaitre-Chaboche混合强化模型能很好地反映钢材的循环塑性流动,适用于预测厚壁钢桥墩在超低周疲劳破坏出现之前的滞回性能。
2)采用Ge模型中的局部和非局部损伤法得到的钢桥墩裂纹萌生寿命都对网格尺寸具有敏感性,预测的裂纹萌生寿命都随着网格加密区的网格尺寸减小而减小。
3)从局部损伤法与非局部损伤法的计算结果对比可以看出,非局部损伤法对于网格尺寸的敏感性相对较小。网格尺寸为2 mm×2 mm的非局部损伤法比较适用于预测钢桥墩的裂纹萌生寿命。
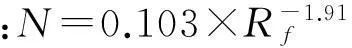
参考文献:
[1]KURODA M.Extremely low cycle fatigue life prediction based on a new cumulative fatigue damage model[J].International Journal of Fatigue,2002,24(6):699-703.
[2]SHIMADA K,KOMOTORI J,SHIMIZU M,et al.The applicability of the Manson-Coffin law and Miner’s law to extremely low cycle fatigue[J].Transactions of the Japan Society of Mechanical Engineers (Part A),1987,53(491):1178-1185.
[3]NIP K H,GARDNER L,DAVIES C M,et al.Extremely low cycle fatigue tests on structural carbon steel and stainless steel[J].Journal of constructional steel research,2010,66(1):96-110.
[4]廖芳芳,王 伟,陈以一,等.往复荷载下钢结构节点的超低周疲劳断裂预测[J].同济大学学报:自然科学版,2014, 42(4):539-546.
[5]XUE L.A unified expression for low cycle fatigue and extremely low cycle fatigue and its implication for monotonic loading[J].International Journal of Fatigue,2008,30(10):1691-1698.
[6]罗云蓉,王清远.建筑用抗震钢高应变低周及超低周疲劳性能研究进展[J].四川建筑科学研究,2011,37(3): 139-145.
[7]KUWAMURA H,TAKAGI N.Similitude law of prefrace hysteresis of steel members[J].Journal of Structural Engineering,2004,130(5):752-761.
[8]韦尧兵,吕延军.超低周变幅疲劳断裂设计的几个问题[J].甘肃工业大学学报,1998,24(2):109-112.
[9]倪捷, 高圣彬, 葛汉彬.锈蚀对外包钢板加固钢筋混凝土桥墩的影响[J].河北工程大学学报: 自然科学版, 2014, 31(4): 25-30.
[10]ZhOU H,WANG Y,SHI Y,et al.Extremely low cycle fatigue prediction of steel beam-to-column connection by using a micro-mechanics based fracture model[J].International Journal of Fatigue,2013(48):90-100.
[11]Ge H,Kang L.A damage index-based evaluation method for predicting the ductile crack initiation in steel structures[J].Journal of Earthquake Engineering,2012, 16(5):623-643.
[12]GE H,KANG L,TSUMURA Y.Extremely low-cycle fatigue tests of thick-walled steel bridge piers[J].Journal of Bridge Engineering,2012,18(9):858-870.
[13]LEMAITRE J,CHABOCHE J L.Mechanics of solid materials [M].Cambridge university press,1994.
[14]石永久,王 萌,王元清,等.结构钢材循环荷载下的本构模型研究[J].工程力学,2012,29(9):92-98.
[15]KANG L,Ge H.Predicting Ductile Crack Initiation of Steel Bridge Structures Due to Extremely Low-Cycle Fatigue Using Local and Non-Local Models[J].Journal of Earthquake Engineering,2013,17(3):323-349.
[16]KAROLCZUK A.Fatigue life estimation under variable amplitude bending using the non-local damage parameter and multisurface plasticity model[J].International Journal of Fatigue,2011,33(10):1376-1383.
[17]HOWARD I C,Li Z H.Finite element analysis of non- local effects in ductile fracture[J].Fatigue & Fracture of Engineering Materials & Structures,2000,23(10):817-824.
[18]GE H,Tsumura Y.Experimental and analytical study on the evaluation of ductile crack initiation in steel bridge piers[J].Journal of Structural Engineering JSCE A,2009(55):605-616.
(责任编辑李军)
Predicting extremely low-cycle fatigue crack initiation life of thick-walled steel bridge piers
CHI Shi-liang, GAO Sheng-bin
(School of Naval Architecture, Ocean and Civil Engineering,Shanghai Jiaotong University,Shanghai 200240, China)
Abstract:To obtain the extremely low-cycle crack initiation life of thick-walled steel bridge piers, numerical analysis of the thick- walled steel bridge piers is carried out. The hysteretic behaviors of thick-walled steel bridge piers under three different kinds of cyclic loading patterns are predicted by using combined hardening model as constitutive law of steel. Crack initiation life of steel bridge piers corresponding to different mesh sizes is determined by using both local and non-local damage methods in Ge model. Then, some parametric studies are carried out to investigate the effect of radius-thickness ratio and slenderness ratio of the piers on crack initiation life by employing Ge model. The analytical results show that the combined hardening model of steel can accurately predict the hysteretic behavior of thick-walled steel bridge piers, and non-local damage method can be employed to accurately predict the crack initiation life of steel bridge piers. On the basis of parametric analytical results, empirical formulas for predicting the crack initiation life of steel bridge piers are proposed.
Key words:bridge engineering; steel bridge pier; parametric study; Ge model; extremely low-cycle fatigue; fatigue crack initiation life
中图分类号:U443.22
文献标识码:A
文章编号:1673-9469(2016)01-0040-07
doi:10.3969/j.issn.1673-9469.2016.01.010
作者简介:池世粮(1989- ),男,福建福州人,硕士,研究方向为结构工程。
基金项目:上海市科学技术委员会浦江人才计划(08PJ1406400)
收稿日期:2015-11-18

